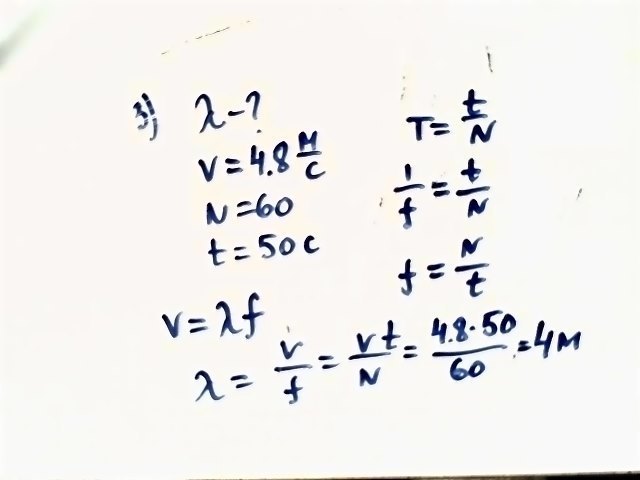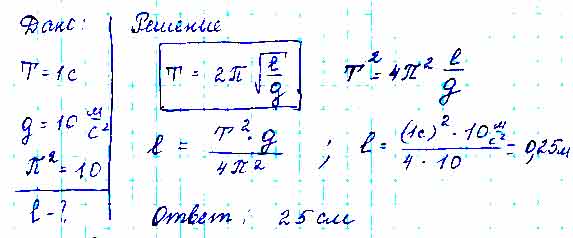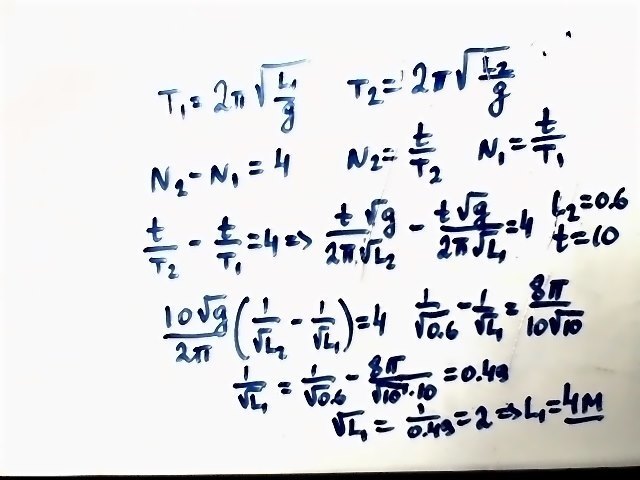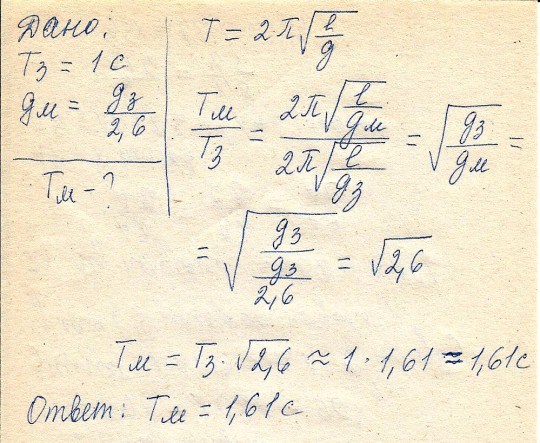Вычислим длину маятника: l = (8/2π)² * 9.8. l ≈ 9.8 метров. Итак, длина математического маятника, совершающего 4 полных колебания за 8 секунд, составляет примерно 9.8 метров.
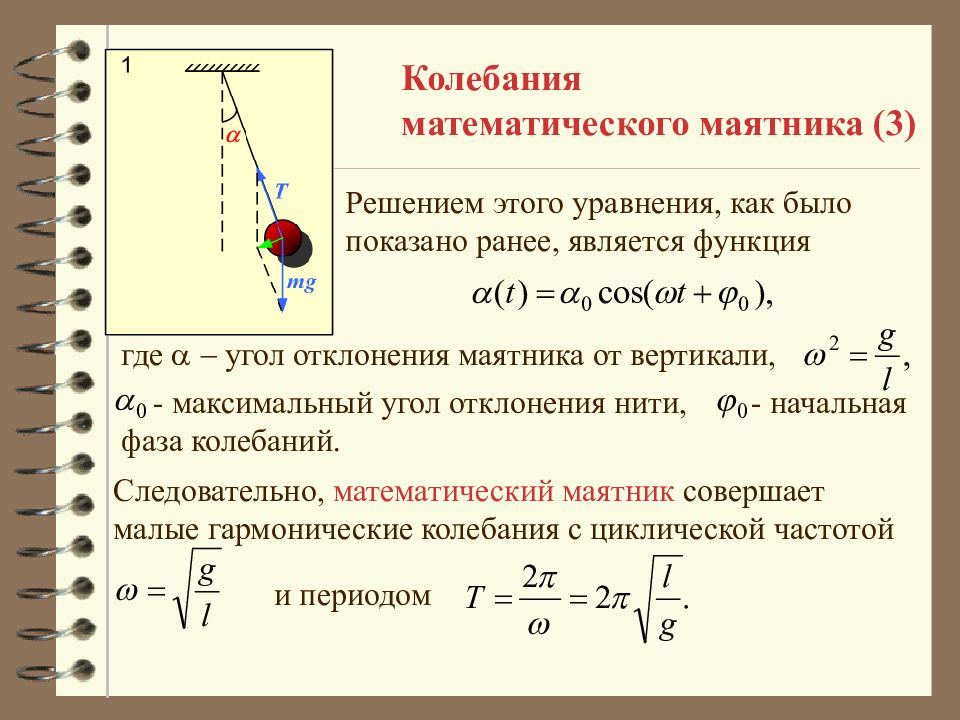
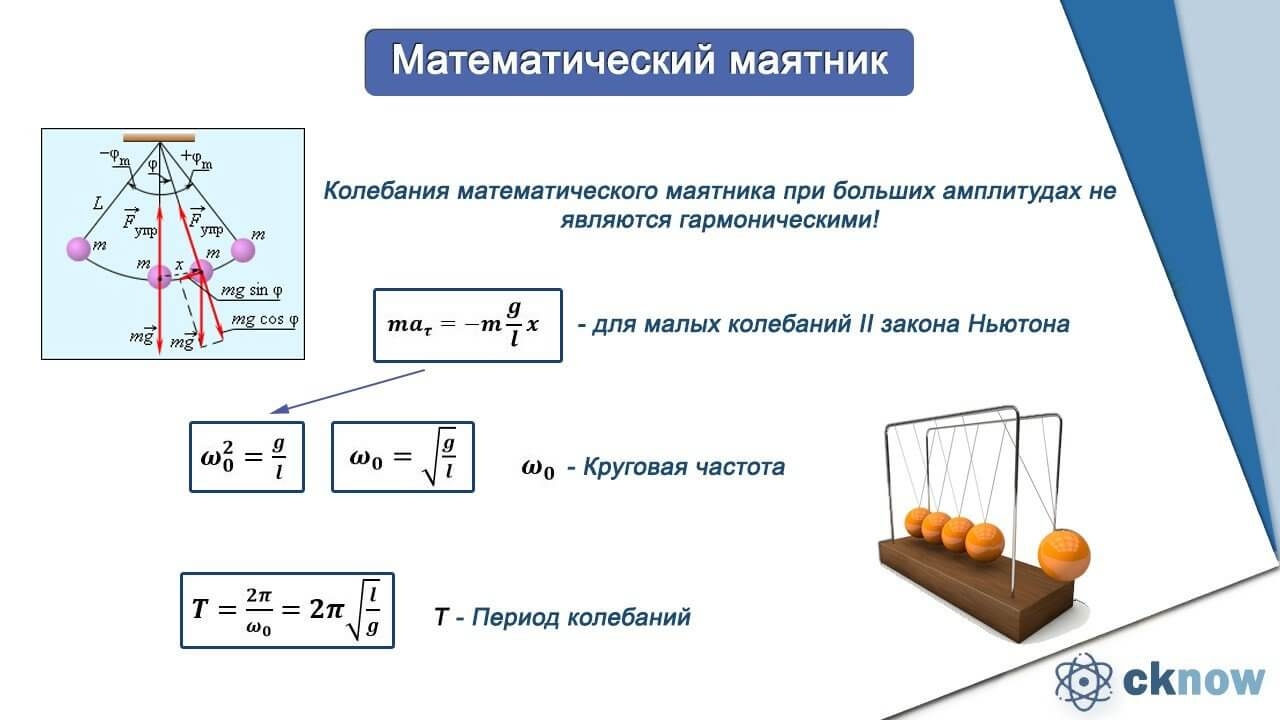
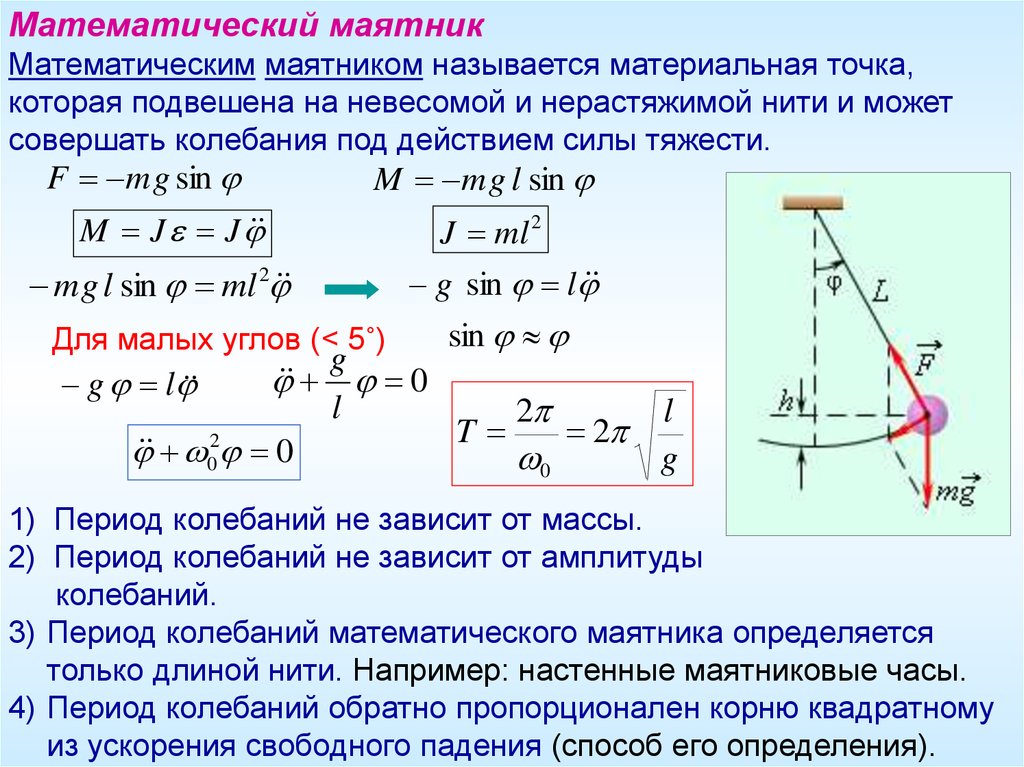
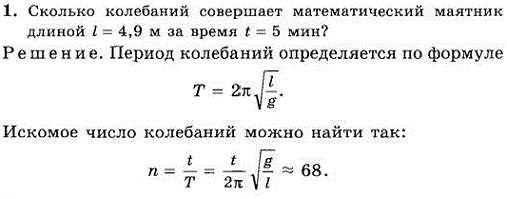В этой формуле \(g\) — ускорение свободного падения (можно принимать \(g=10\) м/с 2), \(l\) — длина нити математического маятника. Возведем обе части уравнения (2) в квадрат: …
Отсюда длина маятника равна l = g*(T/(2π))^2. Период Т равен времени одного полного колебания. Если маятник совершил 4 полных колебаний, то для нахождения периода …
Шарик на нити совершил 60 колебаний за 2 мин. Определите период и частоту …
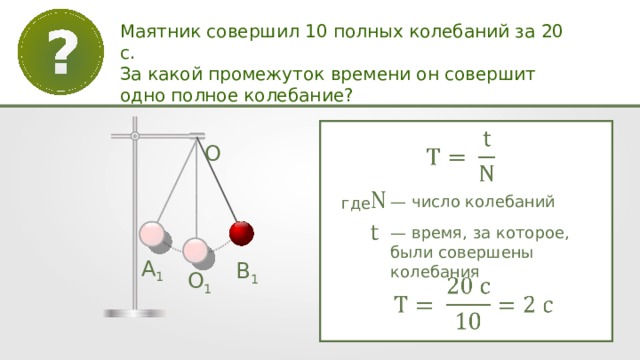
Используем определение периода и формулу периода колебаний математического маятника T= t/N=2 c T=2π√(l/g)
Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, …
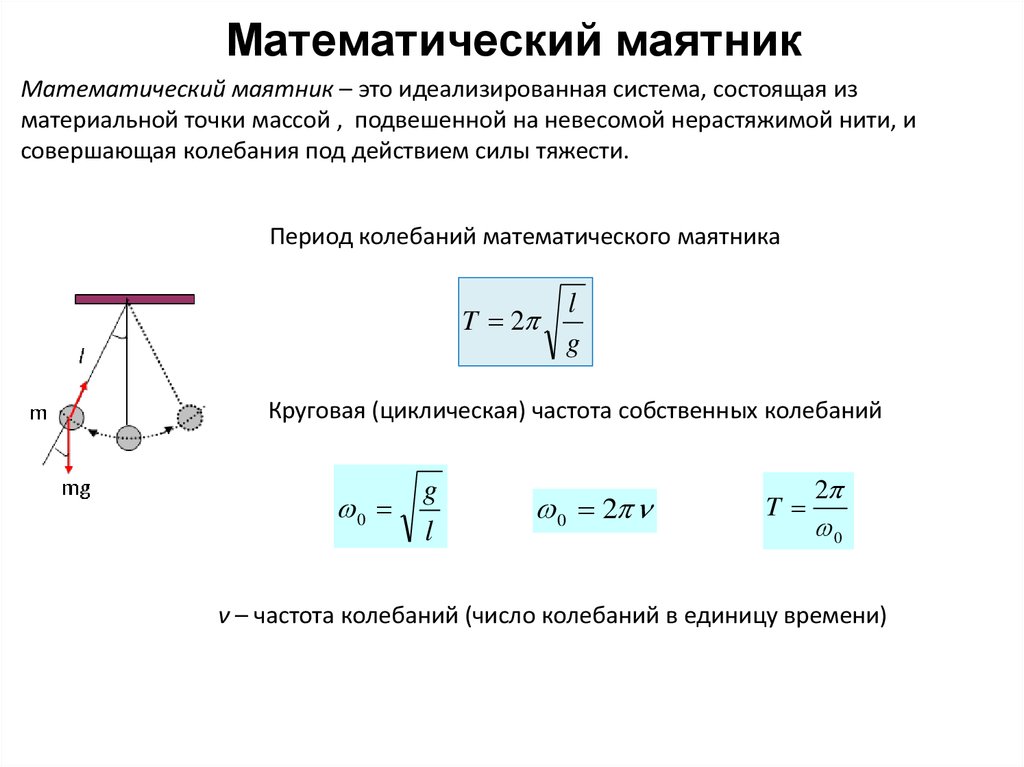
N = 4 t = 8c _____ L - ? Решение: T = t/n = 8c/4 = 2c T = 2п*корень(L/g), L = T^2*g / 4п^2 L = 2^2*10 / 4*3.14^2 = 1 м
9.2.10 Один математический маятник имеет период 3 с, а другой — 4 с. Каков период. 9.2.12 Математический маятник длиной 2,45 м совершает 100 колебаний за 314 с. Определите. …
какова длина математического маятника совершающего 4полных колебания за 8 секунд - ответ на этот и другие вопросы получите онлайн на сайте Uchi.ru
6)Какова длина математического маятника, совершающего гармонические колебания с частотой 1? (Ускорение свободного падения 2 м/с2 ). 7)Частота колебаний равна 12 Гц.
Определите длину математического маятника, который за 10 с совершает на 4 полных колебания меньше, чем математический маятник длиной 60 см.
Формула для определения частоты колебаний математического маятника: ν=(1/2π)*√(g/l), где g - ускорение свободного падения, l - длина математического маятника.
Циклическая частота математического маятника определяется формулой: ω = √g/L g - ускорение свободного падения, L - длина маятника. Тогда: f = ω / 2π = 1/2π √g/L; L = g / …
Пользователь musia задал вопрос в категории Другие предметы и получил на него 1 ответ
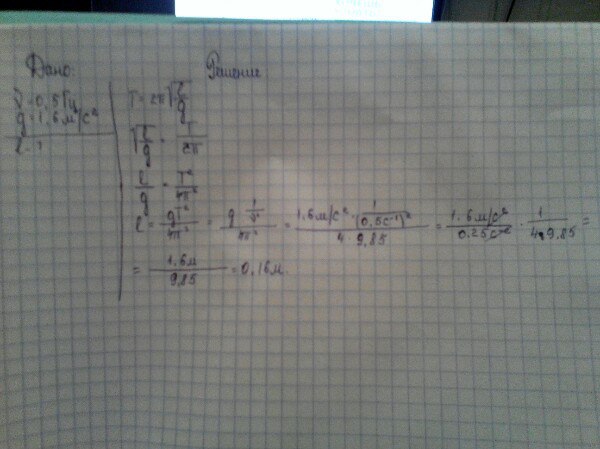
Какова длина математического маятника,совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности …
Еще по теме:
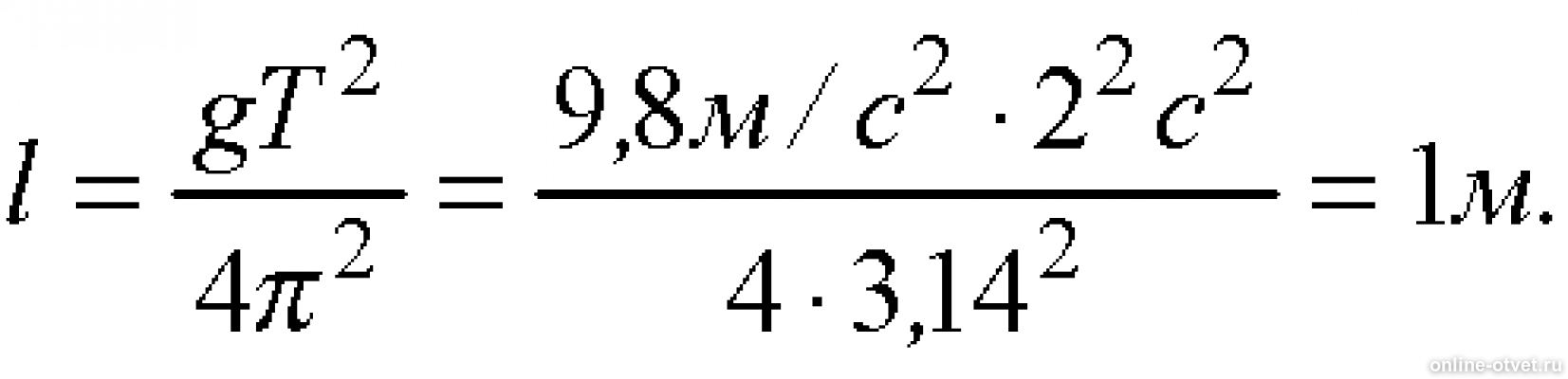
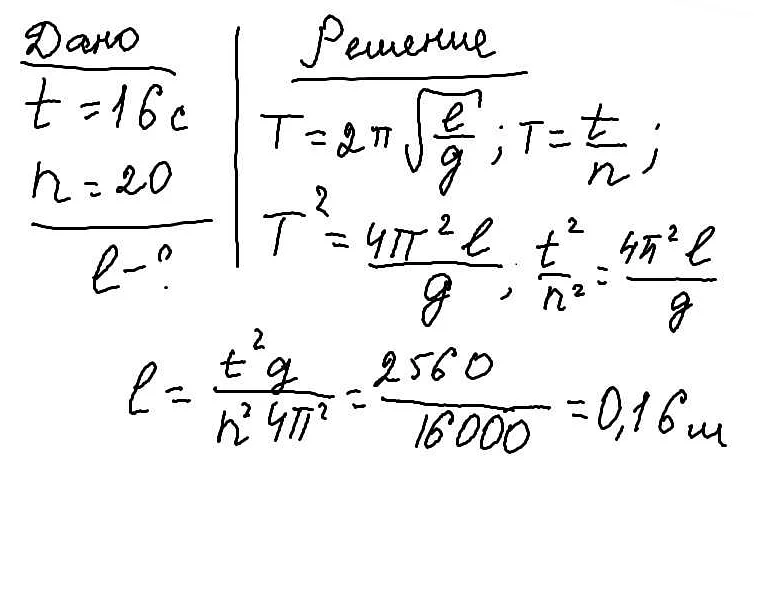
Еще по теме:
