Равнобедренный треугольник – это треугольник, две стороны которого равны, а третья является основанием. See more
Рассмотрим формулы для расчета боковых сторон равнобедренного треугольника. Через основание и высоту Чтобы найти боковые стороны равнобедренного треугольника, …
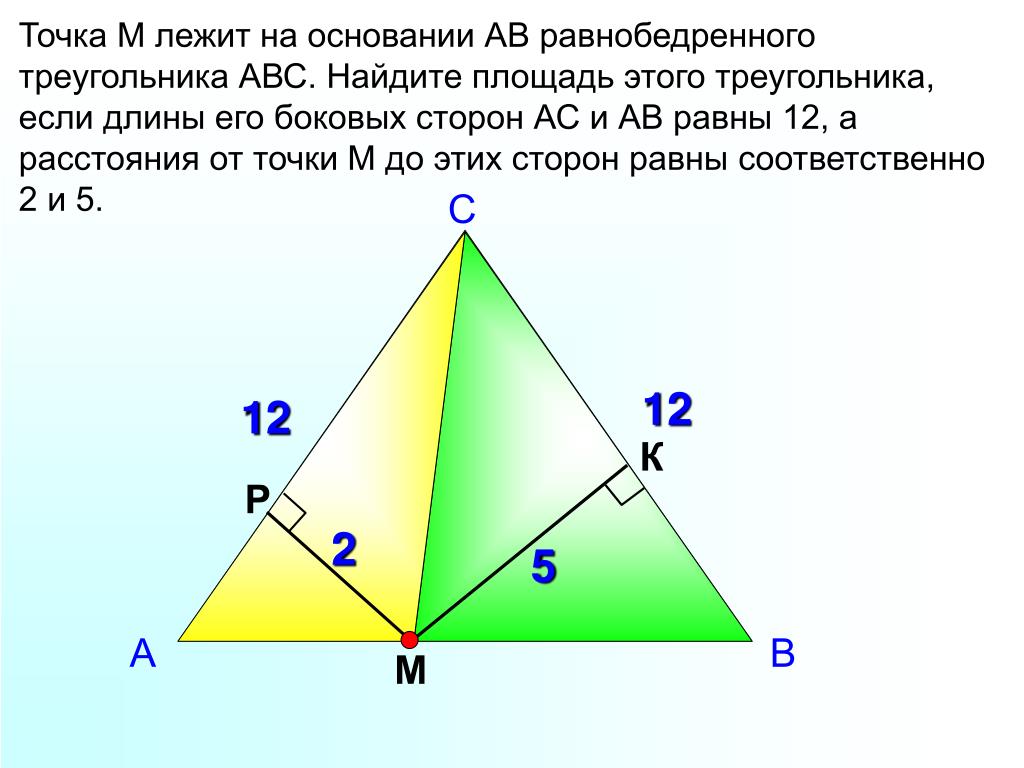
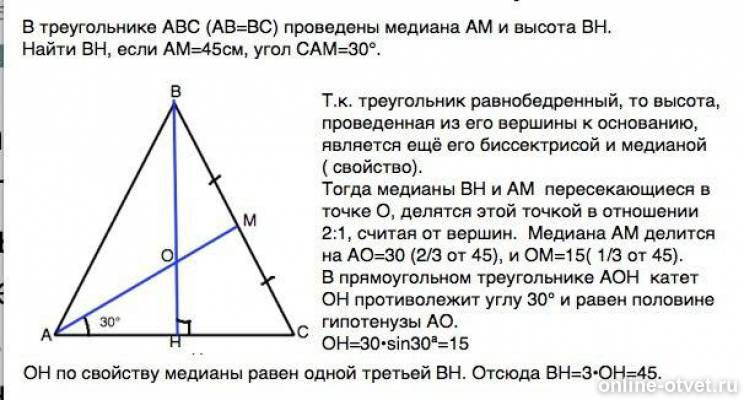
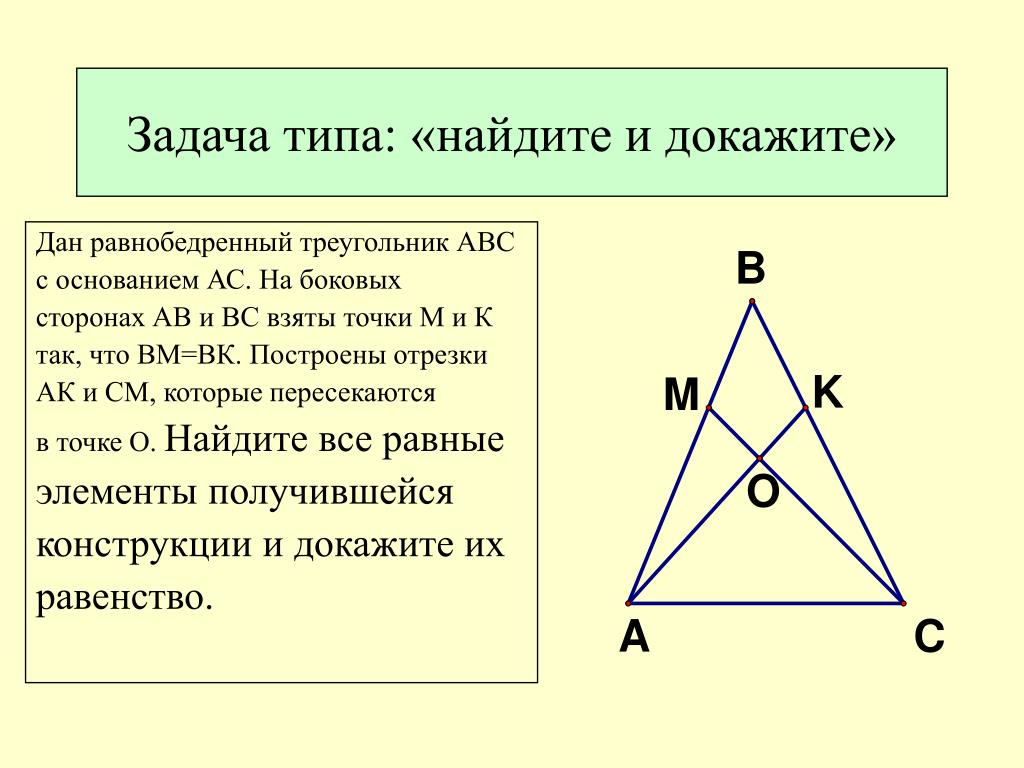
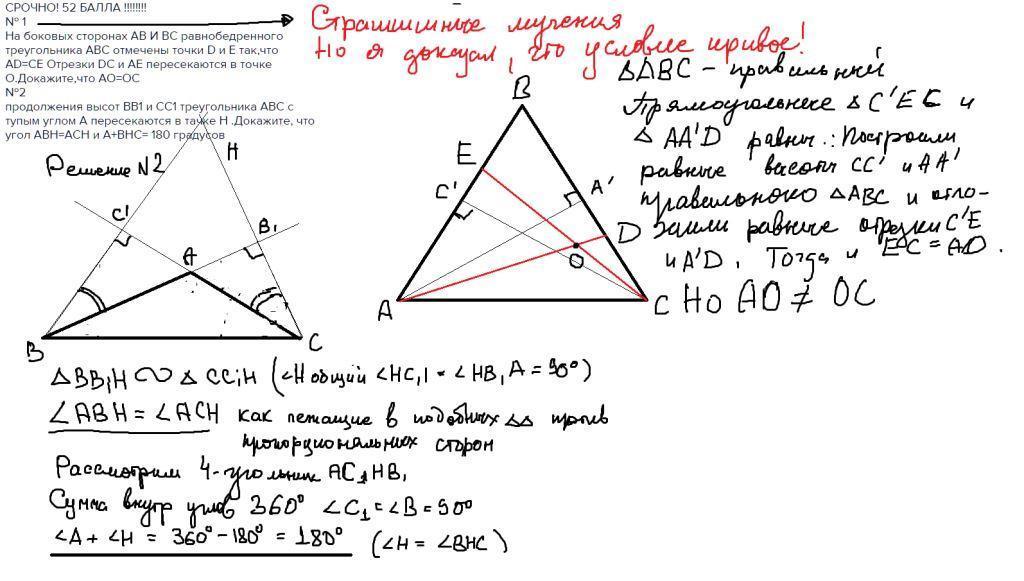
На боковых сторонах равнобедренного треугольника abc отложены равные отрезки bm и bn. Отрезок BD медиана треугольника.
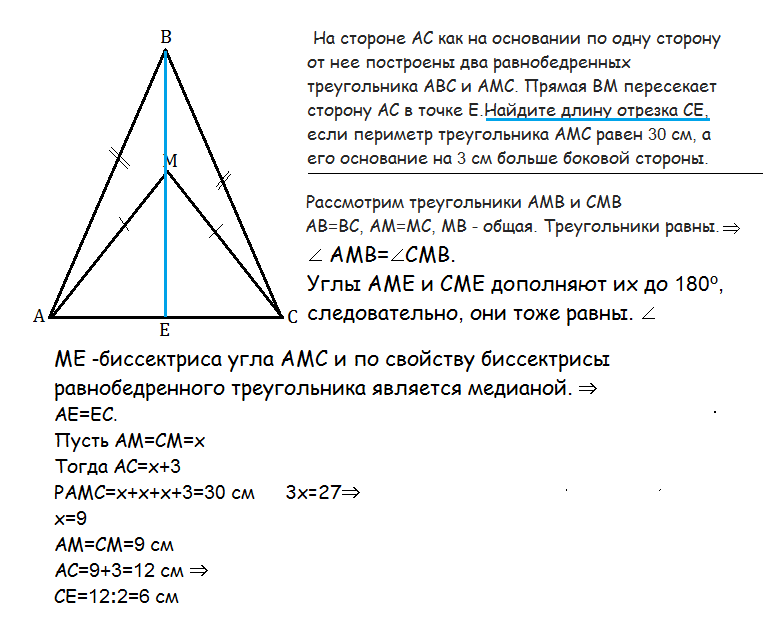
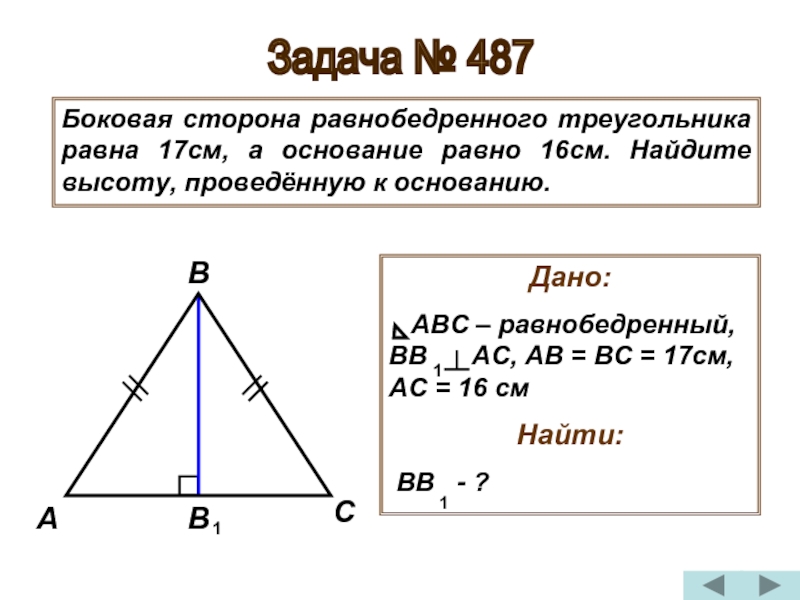
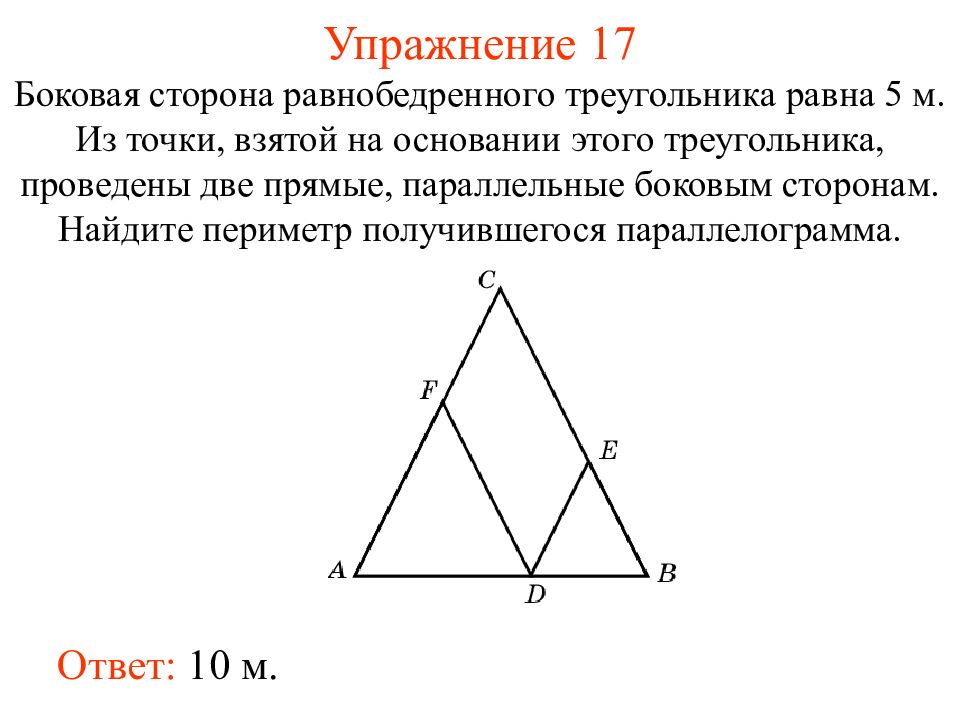
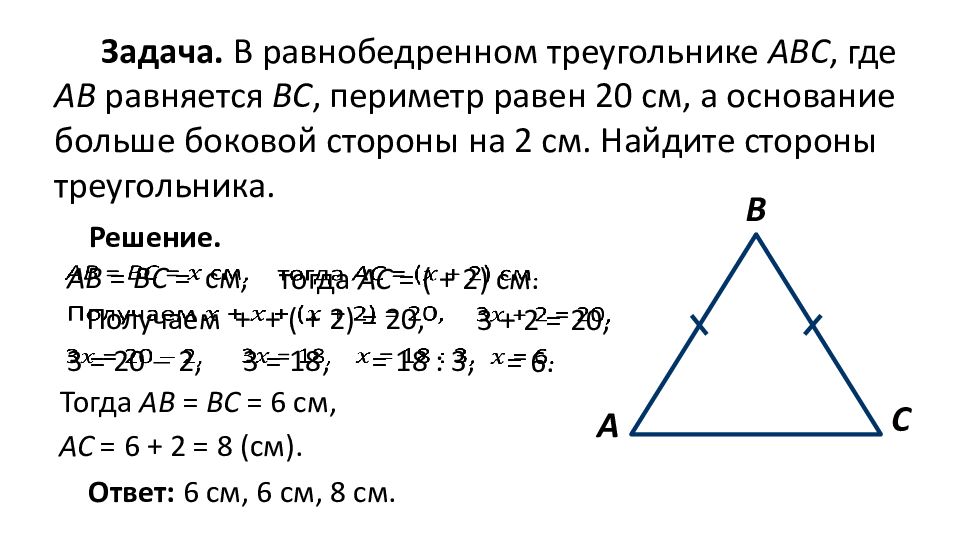
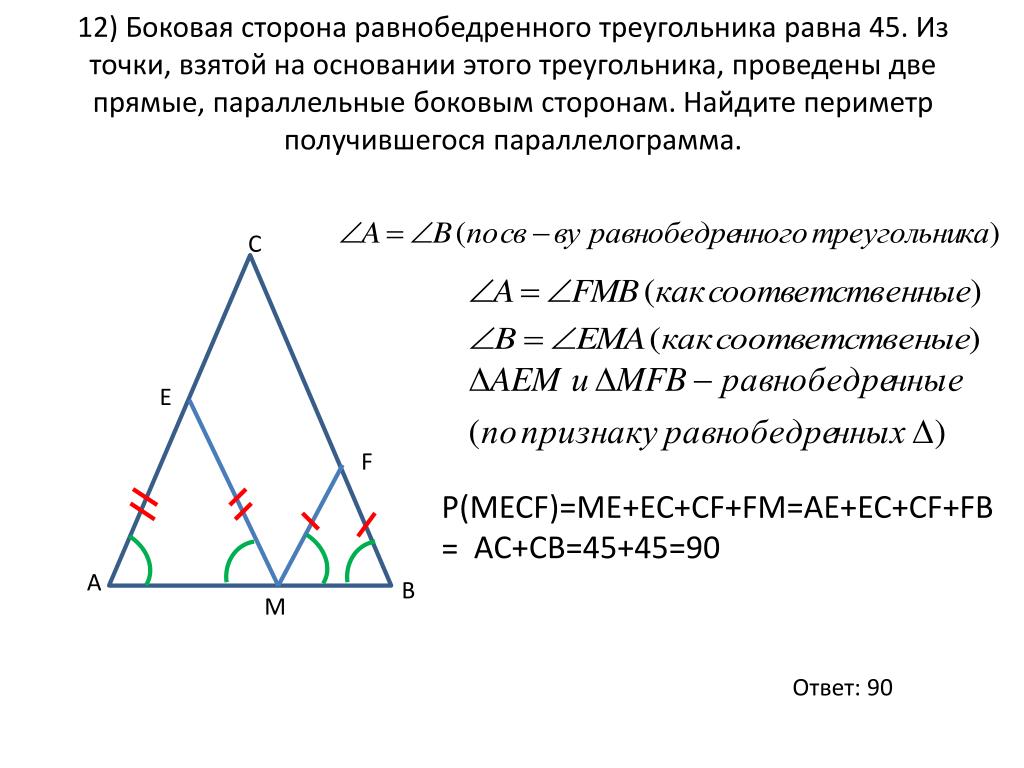
Найдите стороны равнобедренного треугольника, если его периметр равен 30 см, а боковая сторона на 6 см меньше основания.
Угол между боковыми сторонами равнобедненного треугольника (∠A ∠ A ) называется вершинным углом. Углы между основанием и боковыми сторонами (∠B, ∠C ∠ B, ∠ C ) …
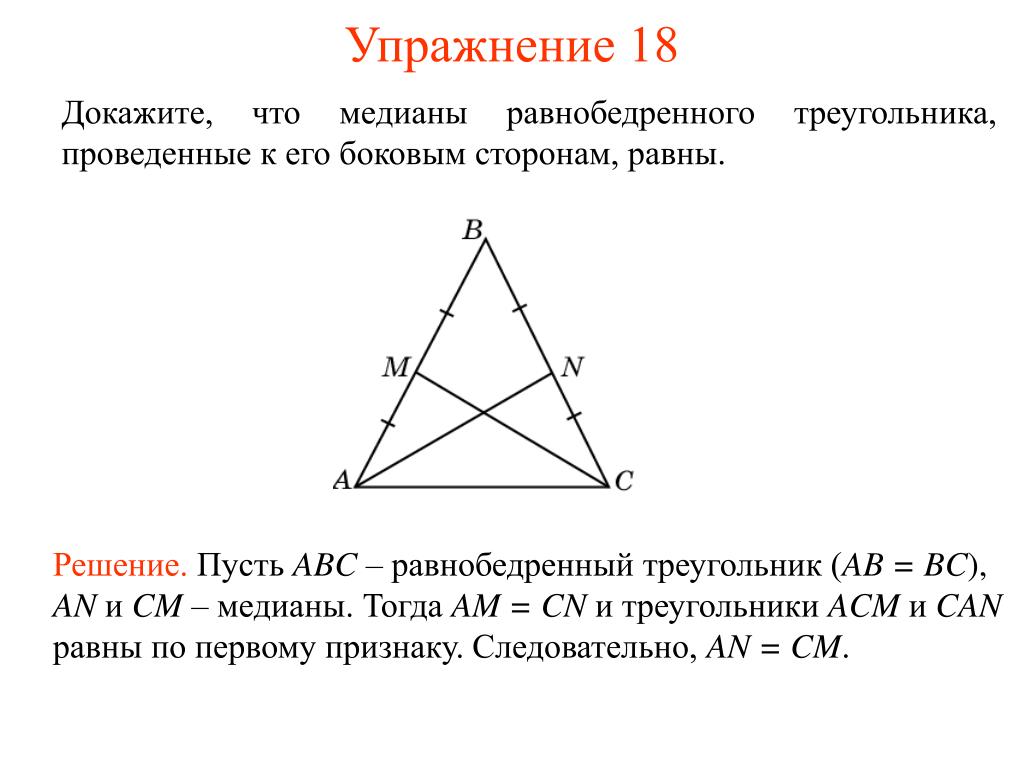
Постройте равнобедренный треугольник, если даны прямая, на которой лежит медиана, проведенная из вершины, две точки на боковых сторонах и точка на основании.
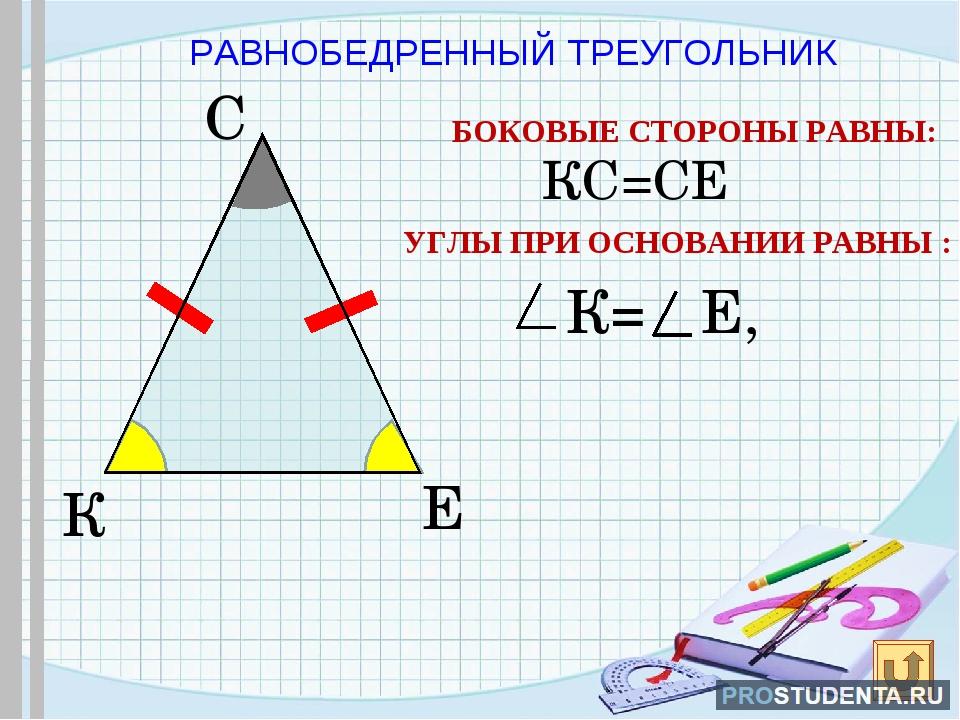
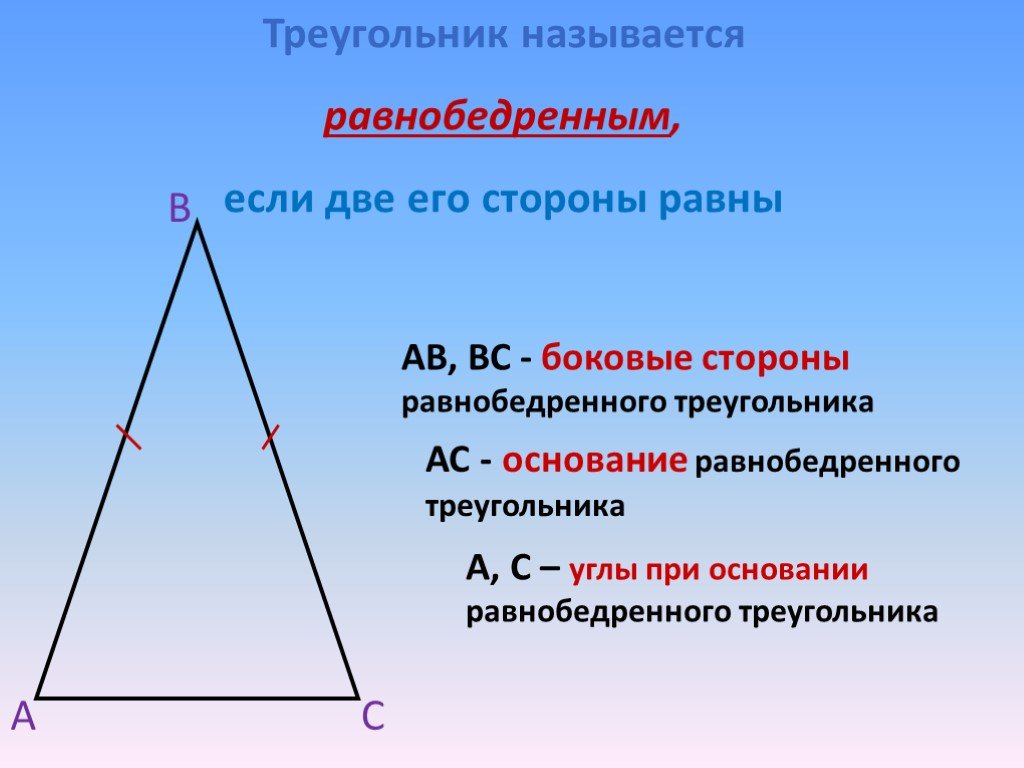
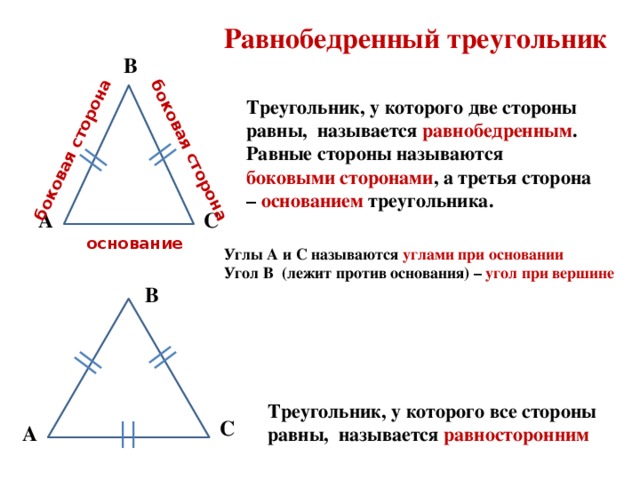
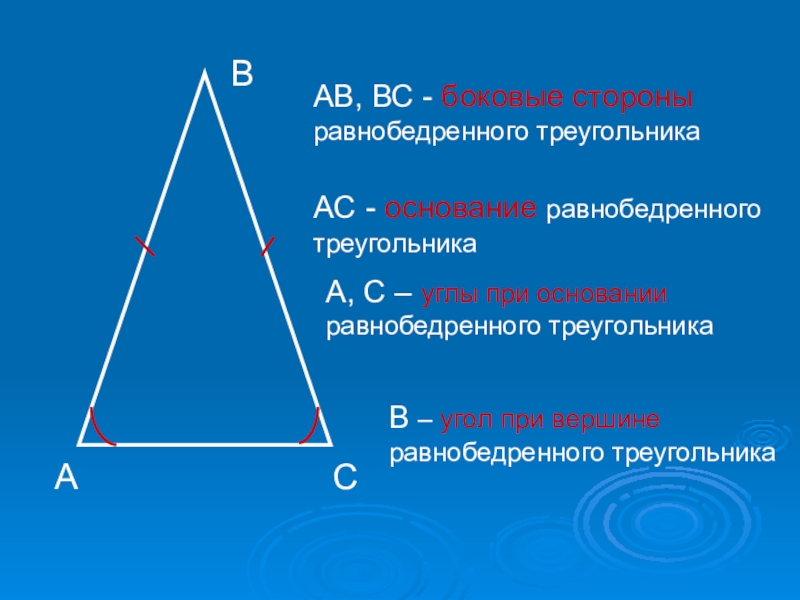
Равнобедренный треугольник - это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
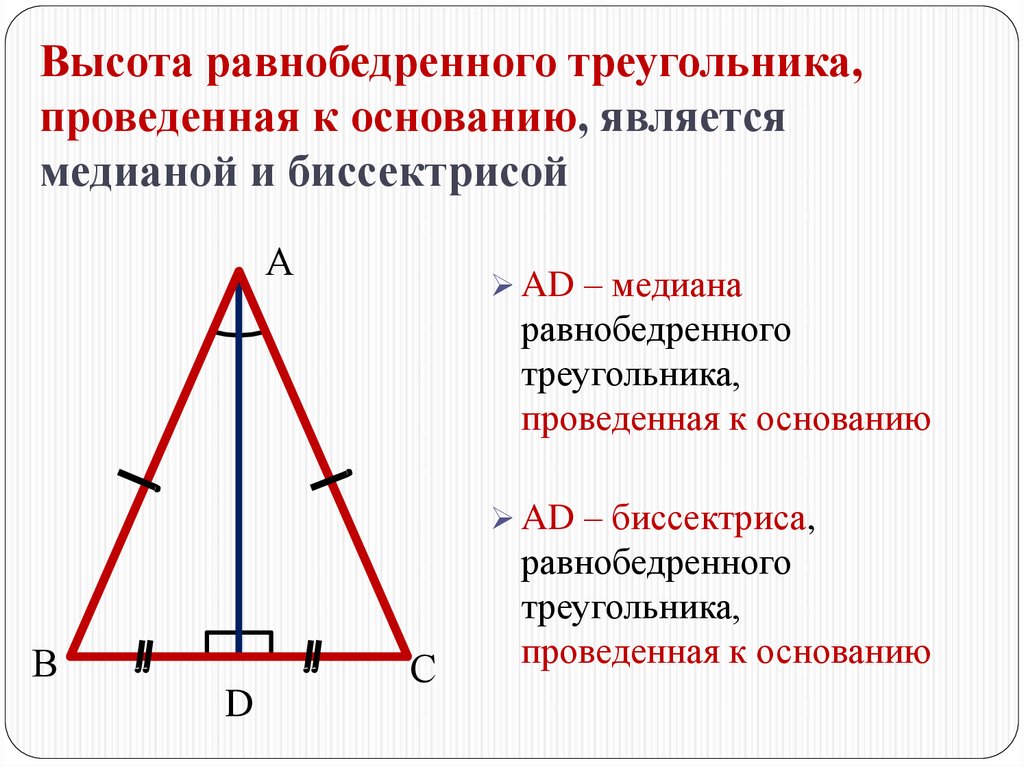
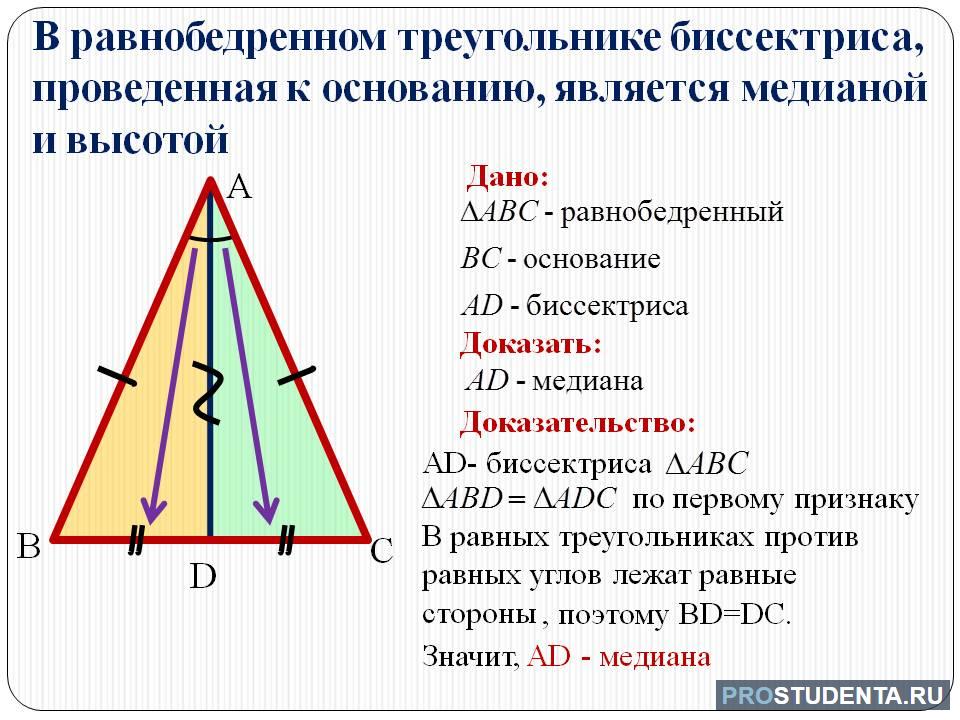
Боковые стороны треугольника равны. Биссектриса треугольника совпадает с медианой и высотой. Углы при основании равнобедренного треугольника равны. Этих свойств вполне достаточно, чтобы использовать стиль …
Равнобедренным называют треугольник, две стороны которого имеют одинаковую длину. Их обозначают как боковые. Третья сторона, которая может быть и длиннее, и короче остальных, называется основанием.
Равнобедренный треугольник — это геометрическая фигура, у которой две стороны равны по длине. Эти стороны называются боковыми, а третья сторона — основанием треугольника (рис. 1). Именно эта …
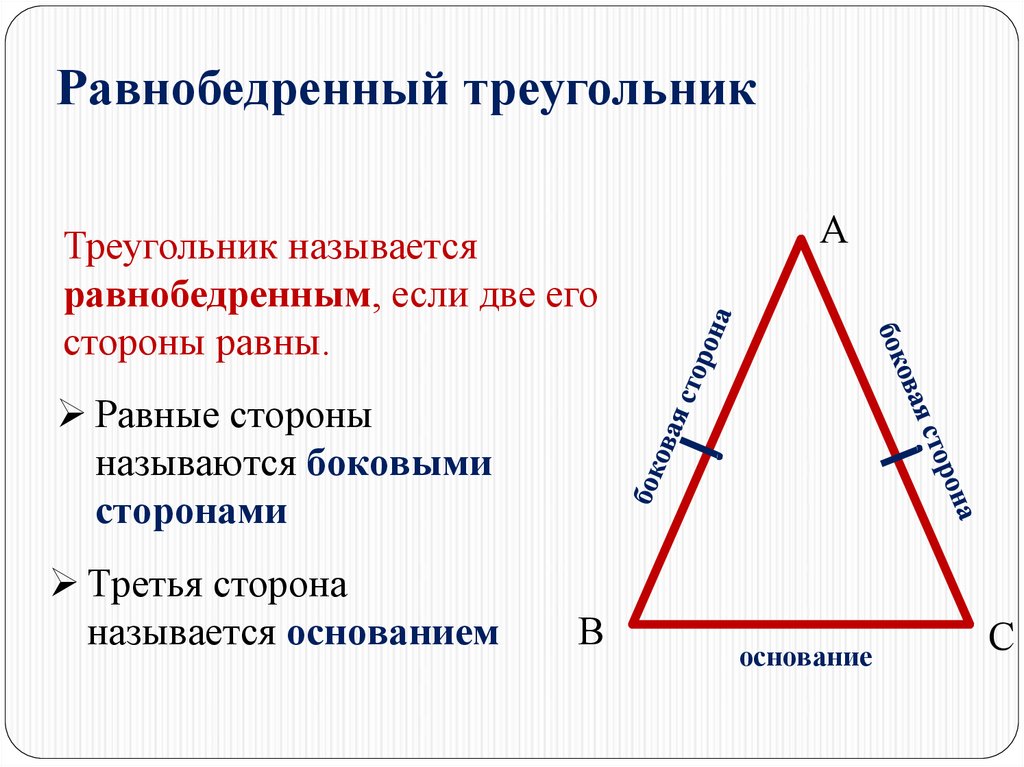
Равнобедренный треугольник — это треугольник, в котором две боковые стороны равны. Боковыми сторонами называются равные стороны, а третья неравная им сторона — основанием.
В 7-м классе на уроках математики ученики знакомятся с различными типами треугольников и их свойствами. Одним из наиболее интересных видов треугольников …
Боковая сторона равнобедренного треугольника может быть найдена по следующей формуле: Формула боковой стороны равнобедренного треугольника через основание и …
На боковых сторонах равнобедренного треугольника МРН (МН — основание) отложены равные отрезки АР и ВР. Найдите длину отрезка АН, если MB = 5 см.
Решение: Имеем формулу радиуса описанной окружности трапеции по сторонам и диагонали: R=adc/4√p (p-a) (p-d) (p-c), где a - боковая сторона, d - диагональ, с - большее …
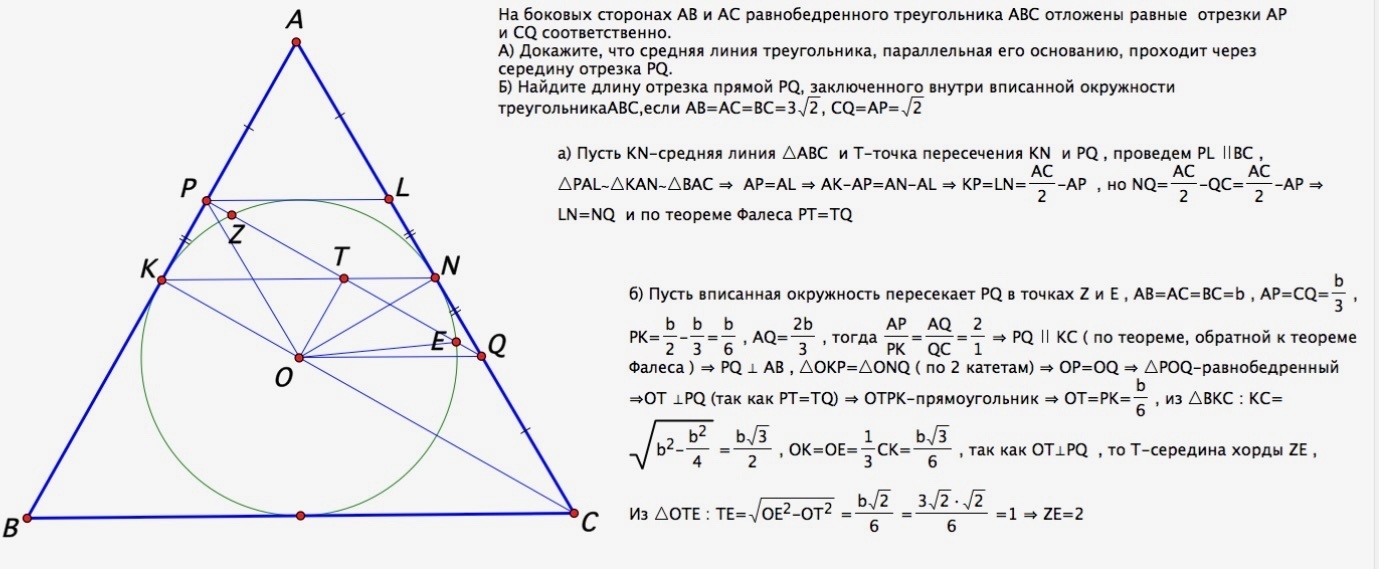
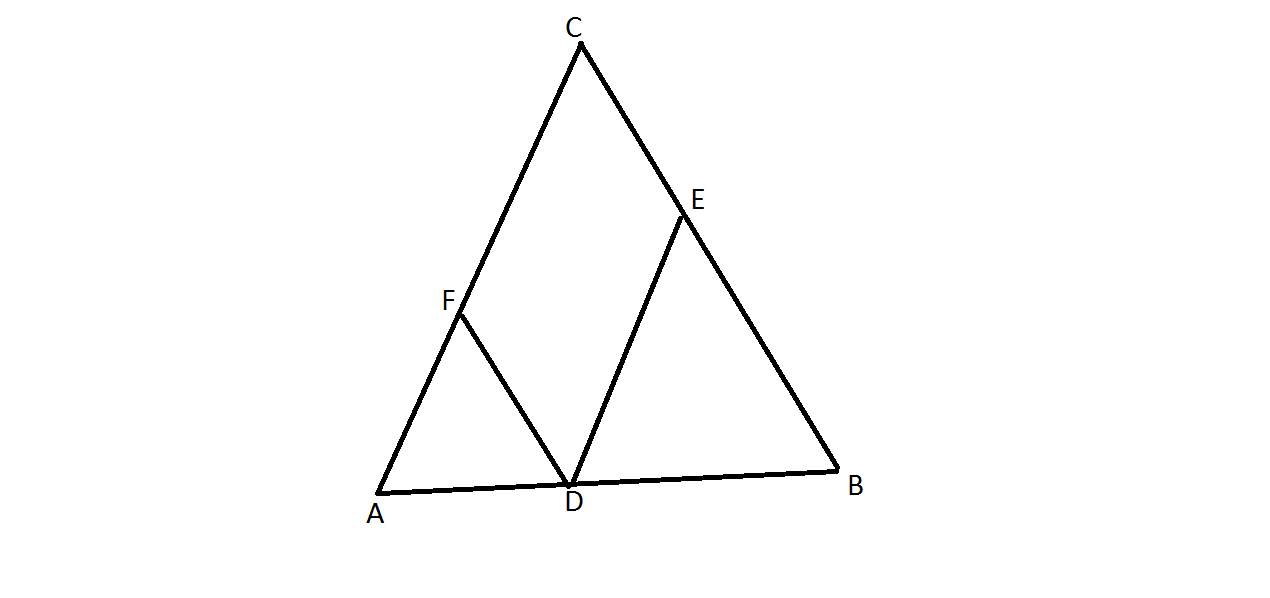На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки АМ и АК. Докажите что треугольник ВСМ=треугольнику СВК.
Еще по теме:
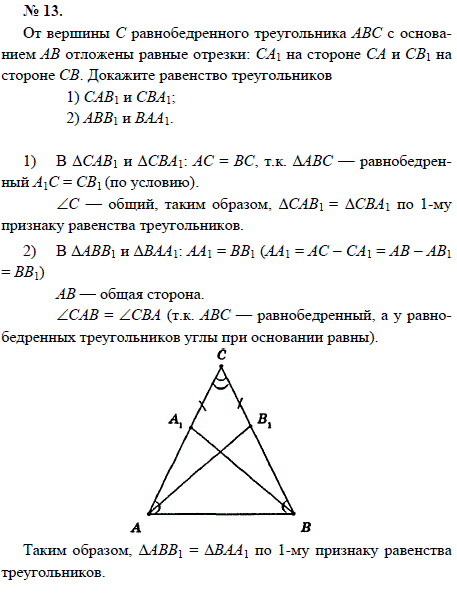
Еще по теме:
