Радиус окружности, вписанной в равнобедренный треугольник, можно найти по стандартной формуле. Свойства равнобедренного треугольника дают возможность получить дополнительные формулы.
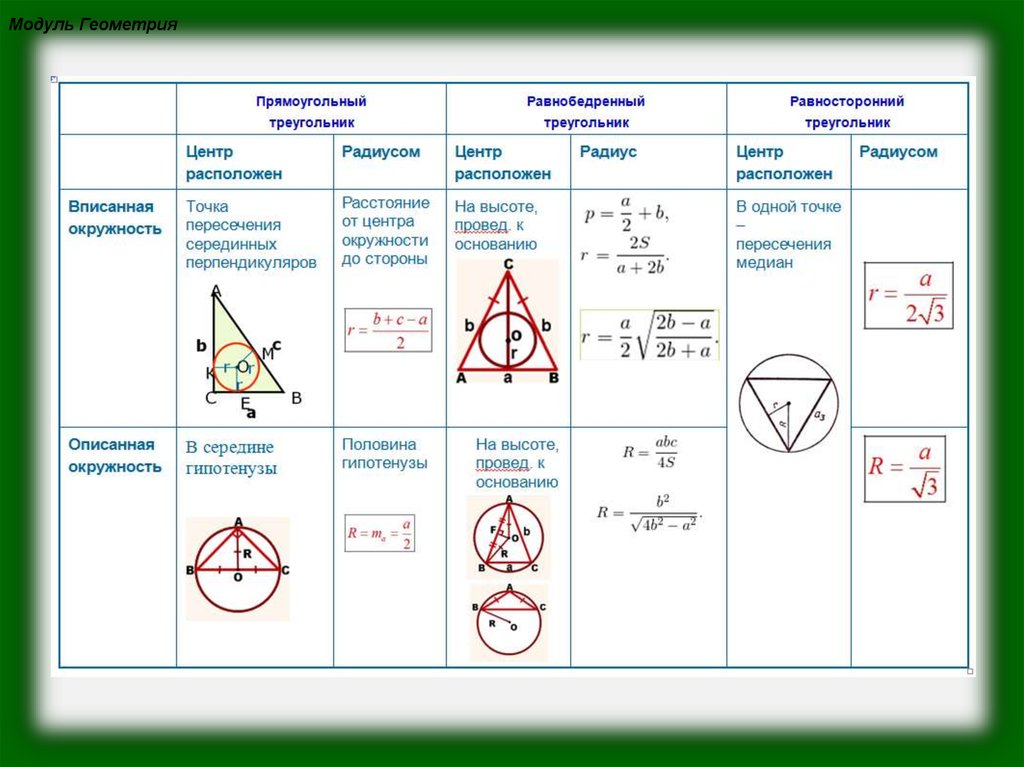
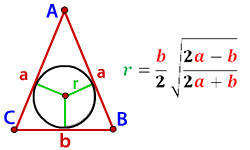Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) : Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной в равнобедренный треугольник окружности, выраженный через боковую сторону и высоту, опущенную на основание: Окружность, вписанная в равнобедренный треугольник. Формула радиуса. …
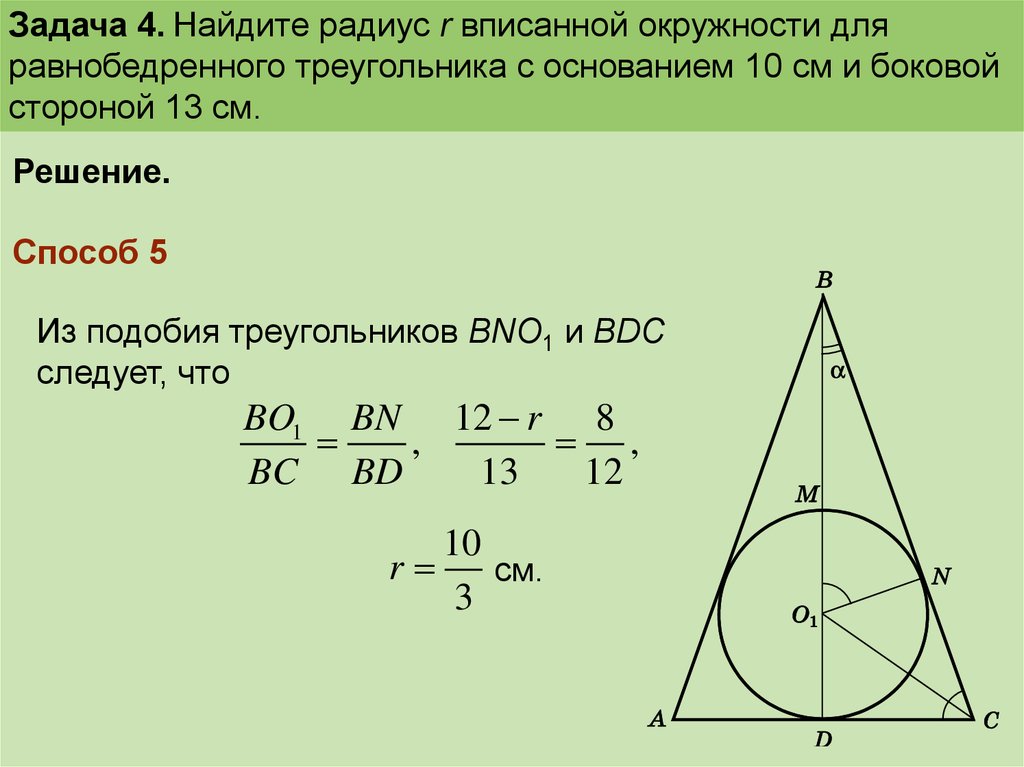Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона. Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем …
Радиус вписанной в равнобедренный треугольник окружности, выраженный через основание и угол при основании: Вписанная в равнобедренный треугольник окружность. Формула радиуса. Рассмотрим равнобедренный …
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) : 2. Формулы радиуса вписанной окружности если известны: сторона …
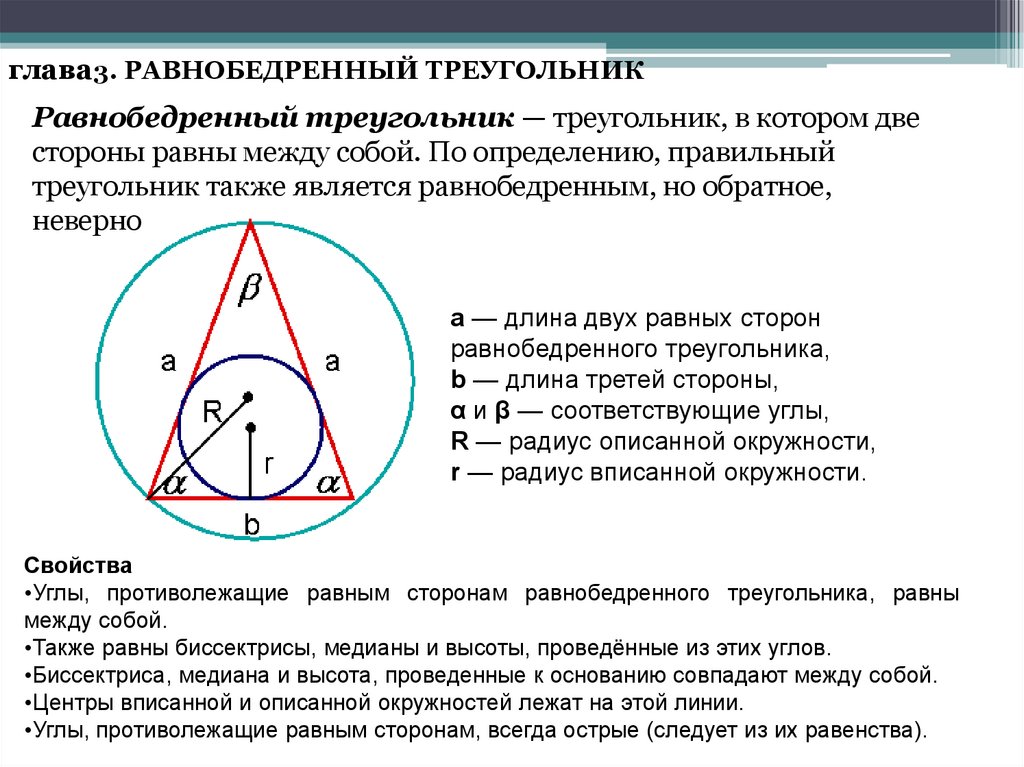
Пусть a — длина равных боковых сторон, b — длина основания, h — высота к основанию, R — радиус описанной окружности. Радиус вписанной окружности может быть выражен …
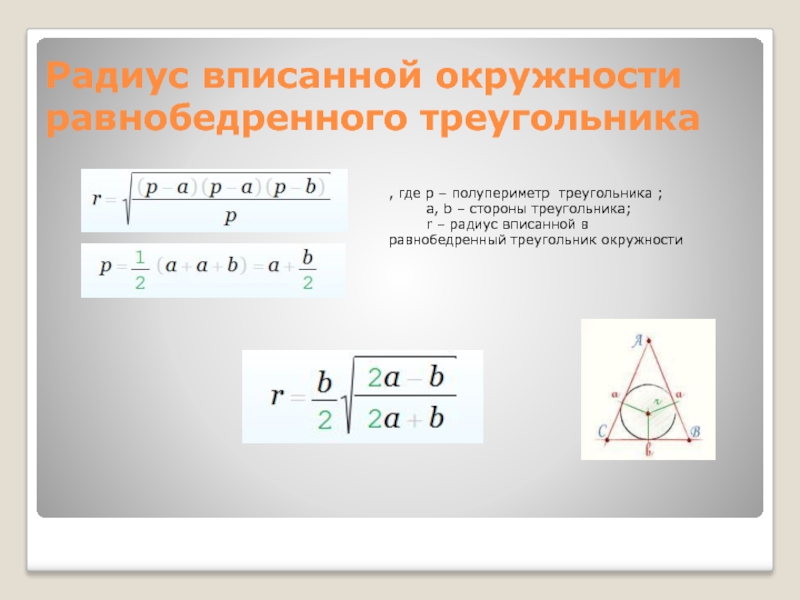
Радиус вписанной окружности равнобедренного треугольника вычисляется по классической формуле \[r = \sqrt{\frac{(p-a)(p-a)(p-b)}{p}}\]
В равностороннем треугольнике, где все три стороны равны (обозначим одну сторону через а), радиус вписанной окружности вычисляется по формуле: Если в треугольнике две стороны равны …
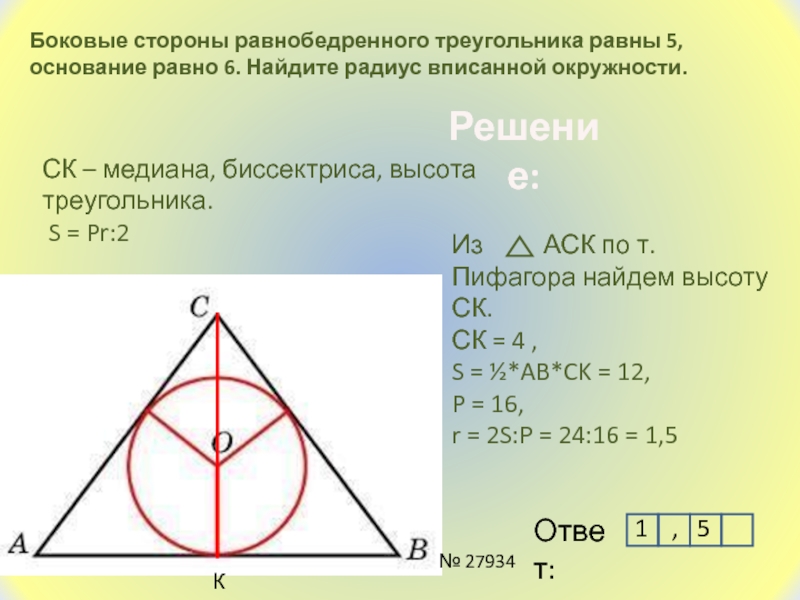
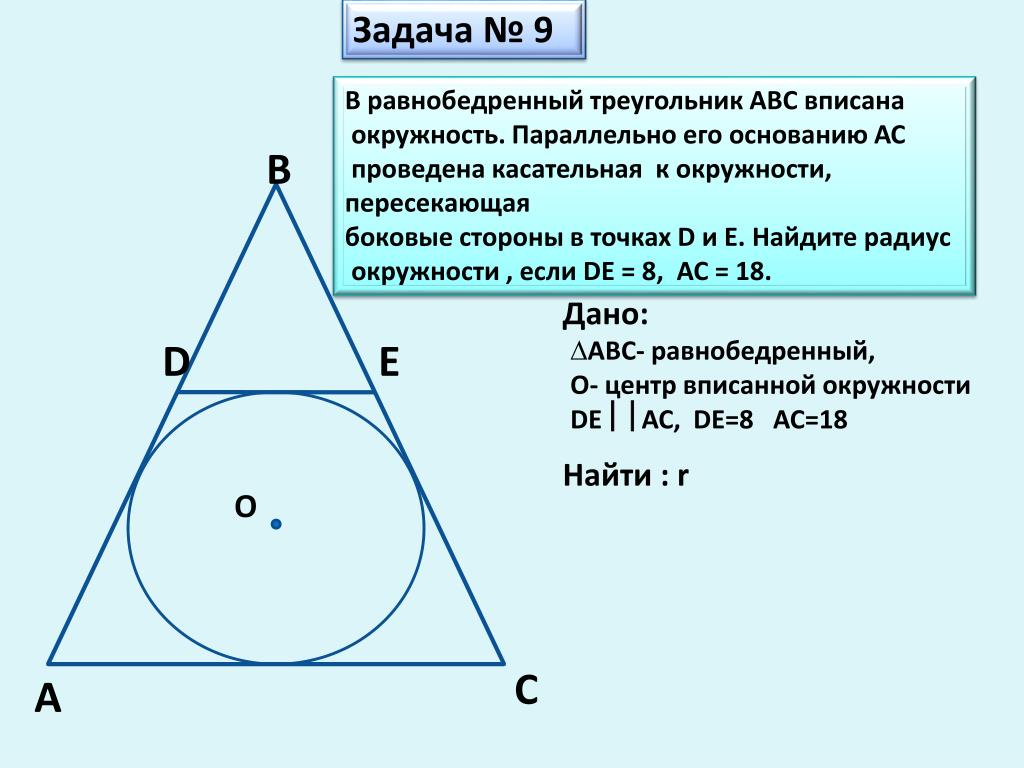
Вывод формулы радиуса вписанной в равнобедренный треугольник окружности. Шаг 1. Рассмотрим равнобедренный треугольник АВС (АВ=ВС). Из вершины B опустим на основание высоту ВК. Пусть в этот треугольник …
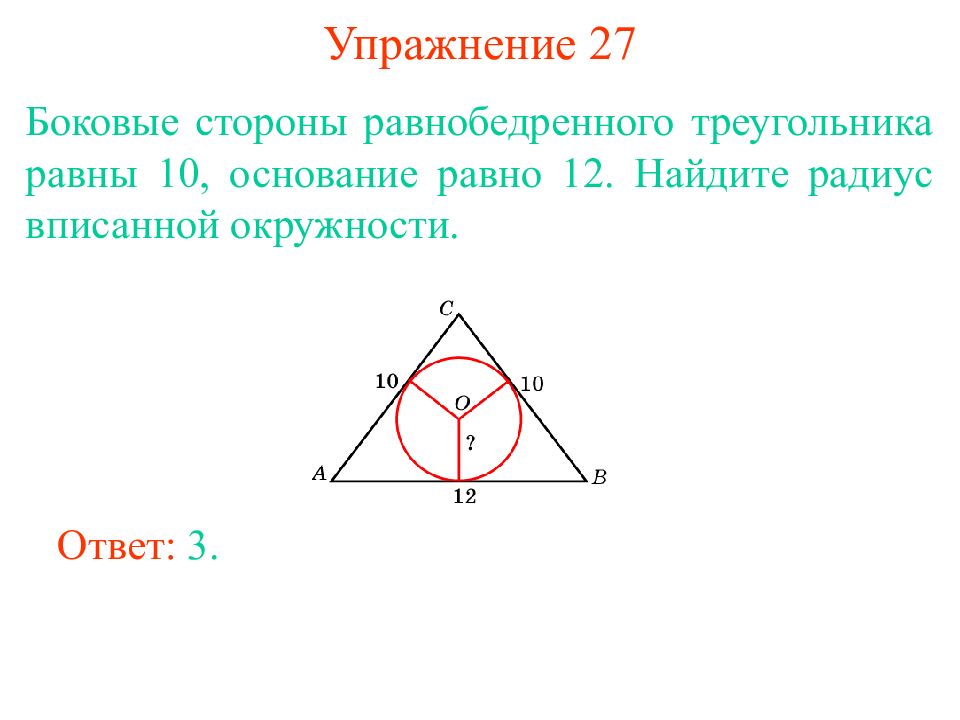
Найти радиус вписанной окружности в равнобедренный треугольник, зная стороны
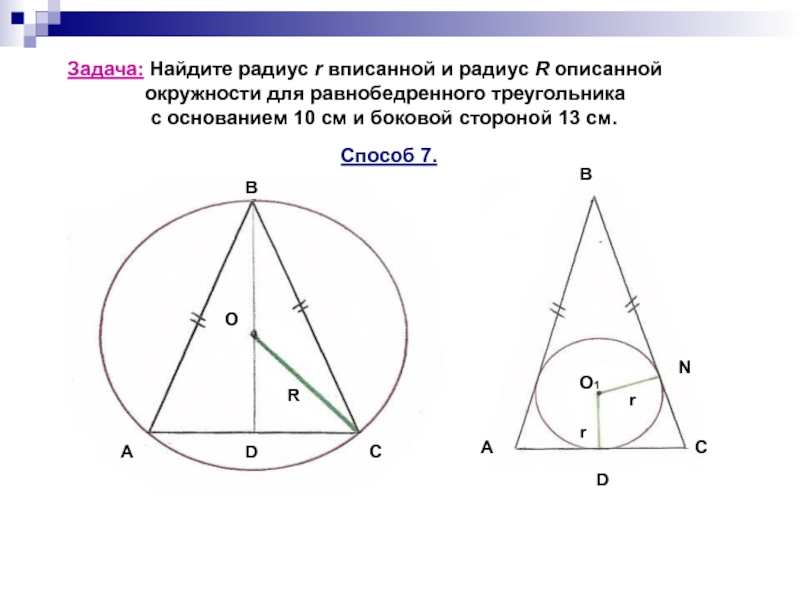В статье подробно описано, как находить радиус вписанной в треугольник окружности с помощью универсальной формулы через площадь и периметр треугольника.
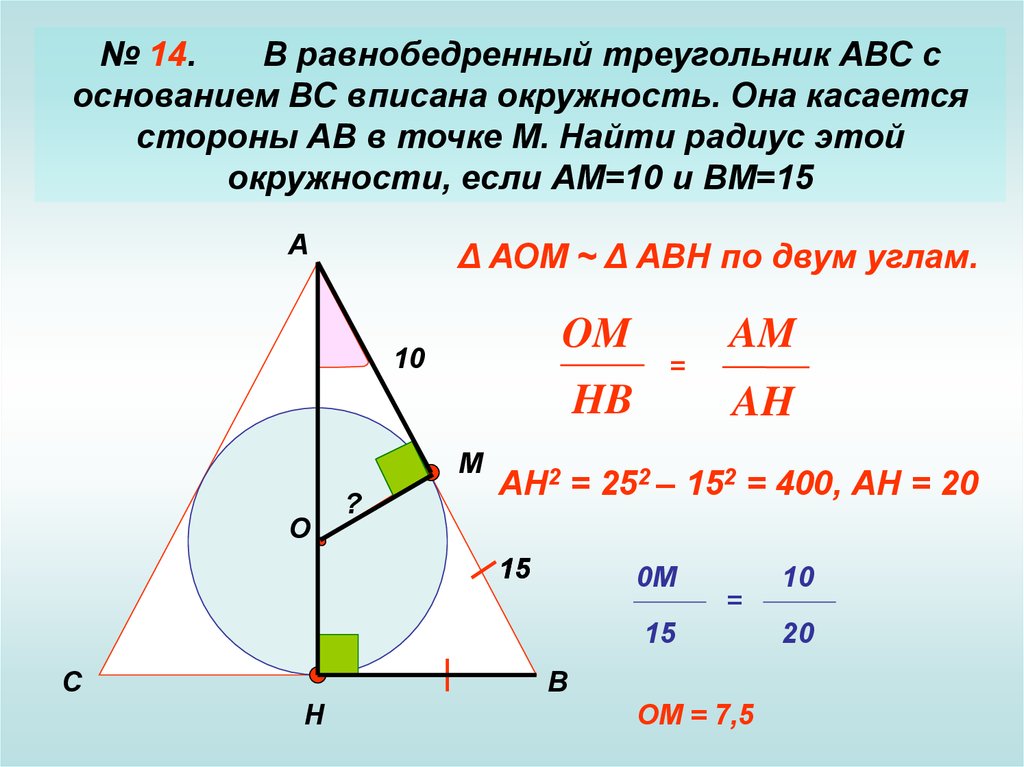
Найдите радиус окружности, вписанной в треугольник, если проведенная к основанию высота равна 16 см. Решение: Из курса геометрии известно, что радиус вписанной в …
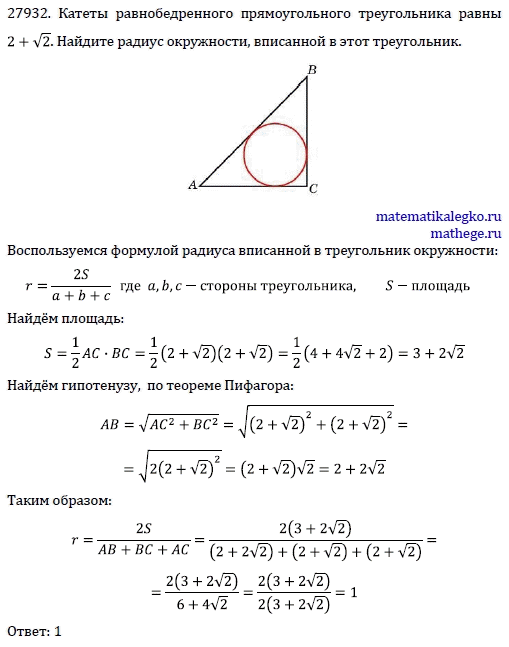
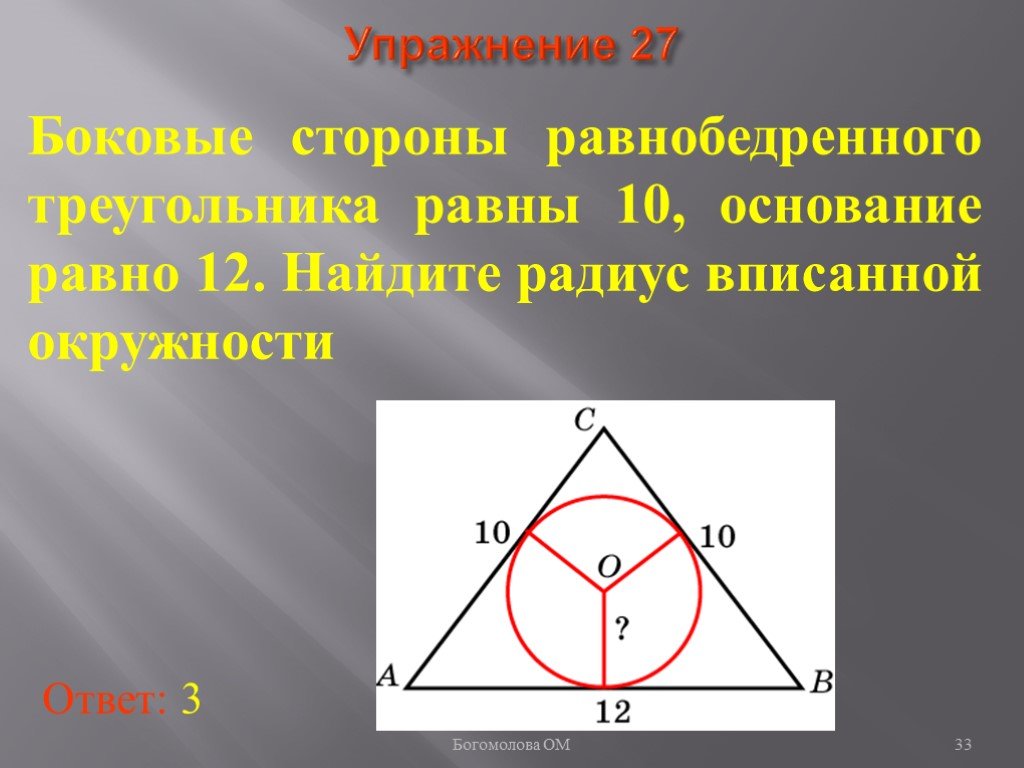Формула для нахождения радиуса окружности, вписанной в прямоугольный треугольник где a и b — катеты, c — гипотенуза.
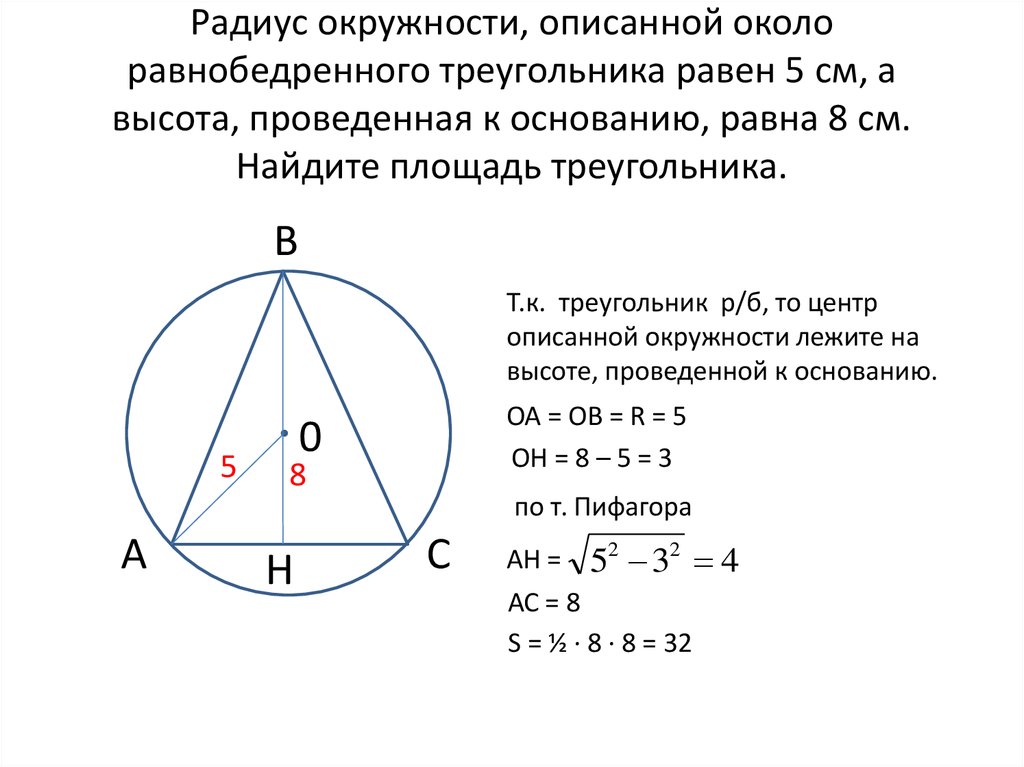
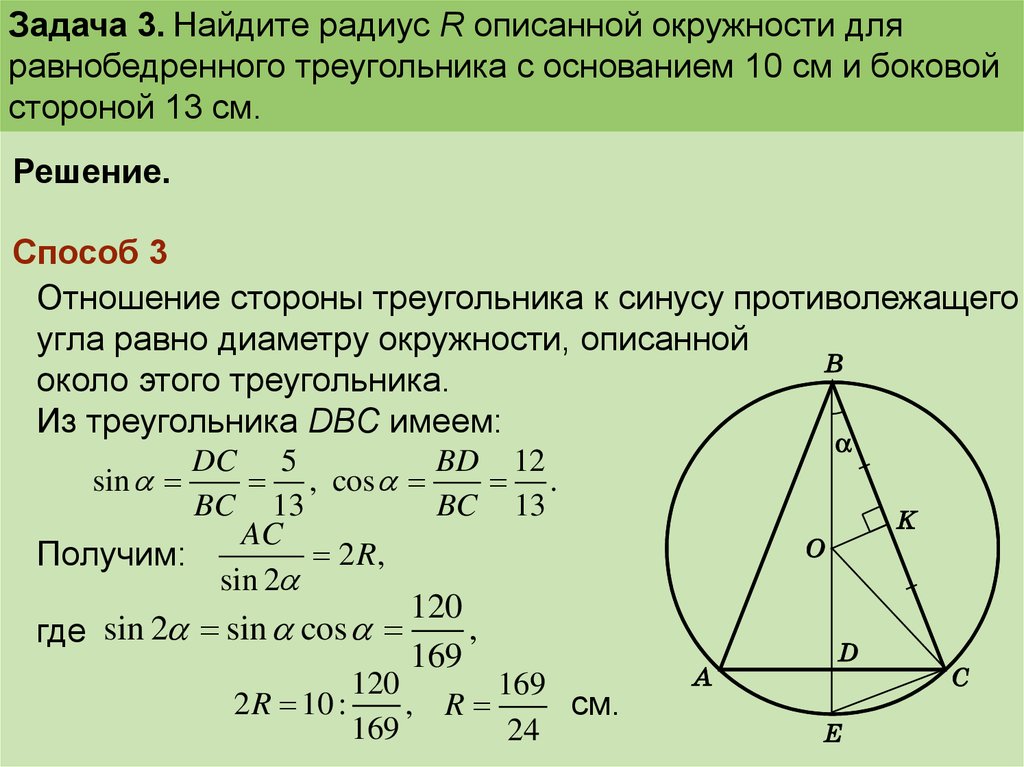
Радиус описанной около равнобедренного треугольника окружности: где a — основание, b — боковая сторона, α — угол при вершине, β — угол при основании.
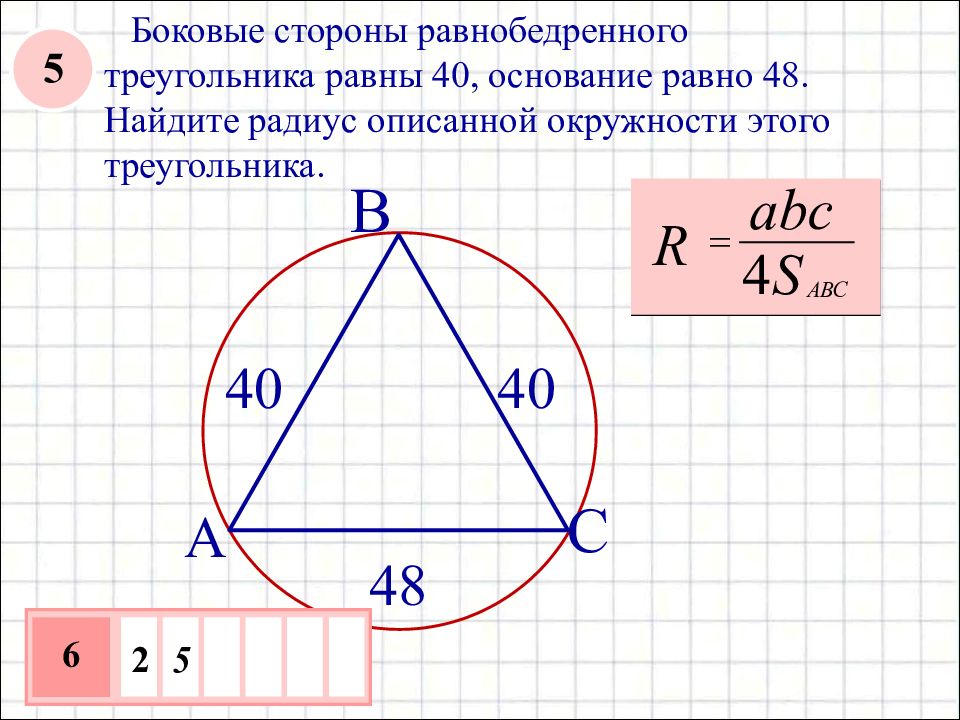
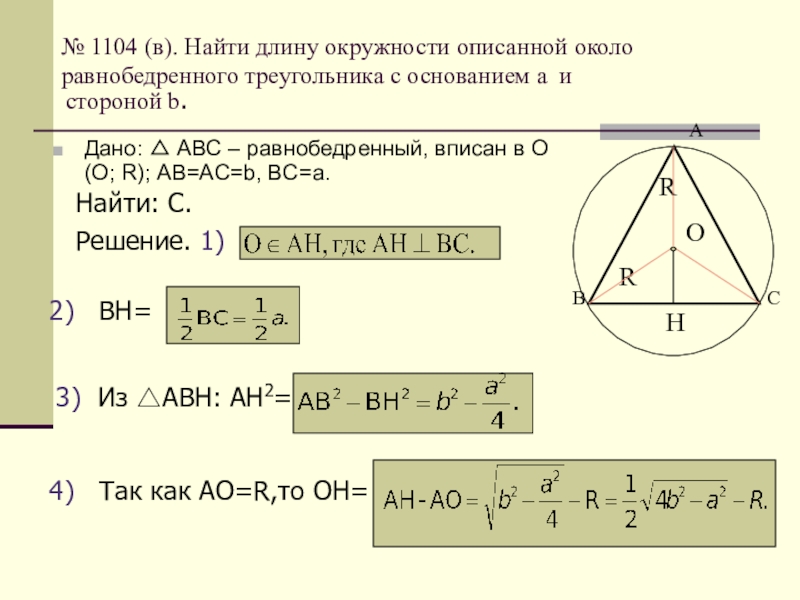
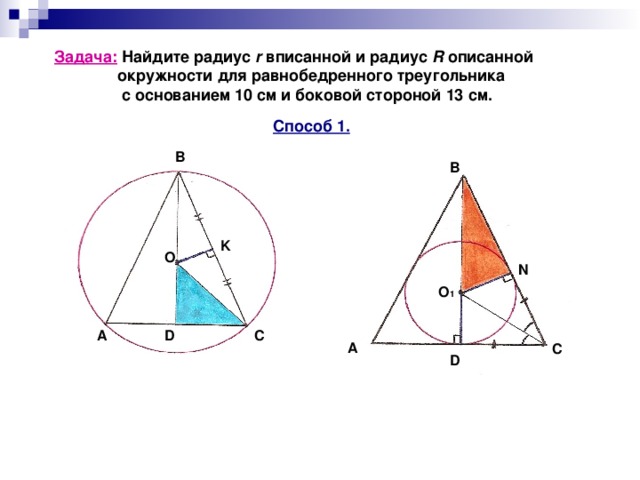Радиус описанной окружности равнобедренного треугольника вычисляется по классической формуле \[ R = \frac{a^2 b}{4\sqrt{p(p-a)(p-a)(p-b)}} \]
Еще по теме:
Еще по теме:
