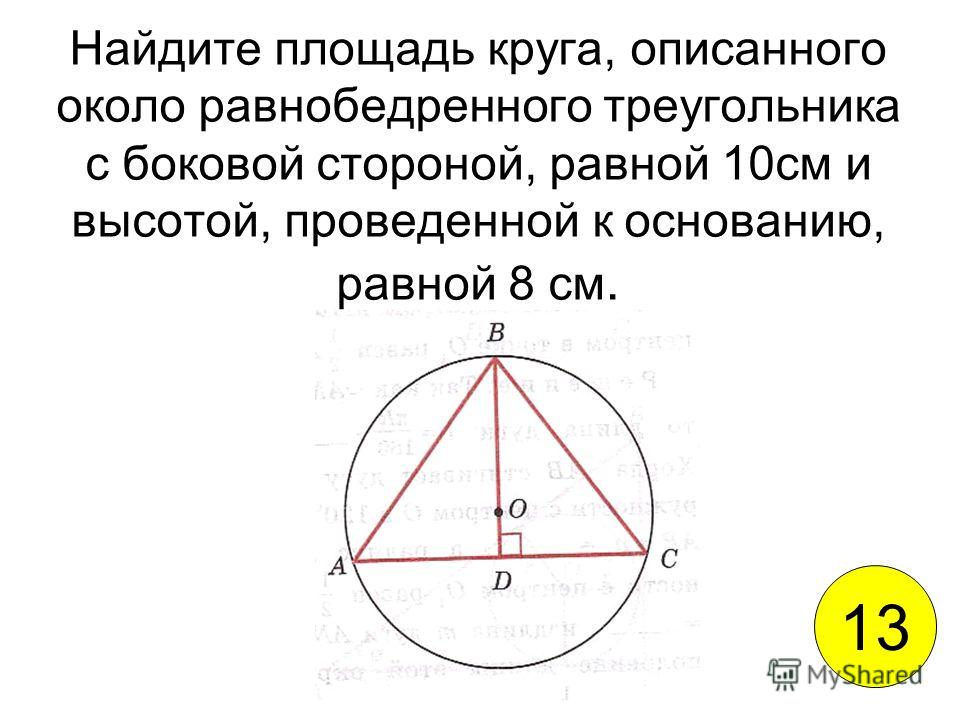
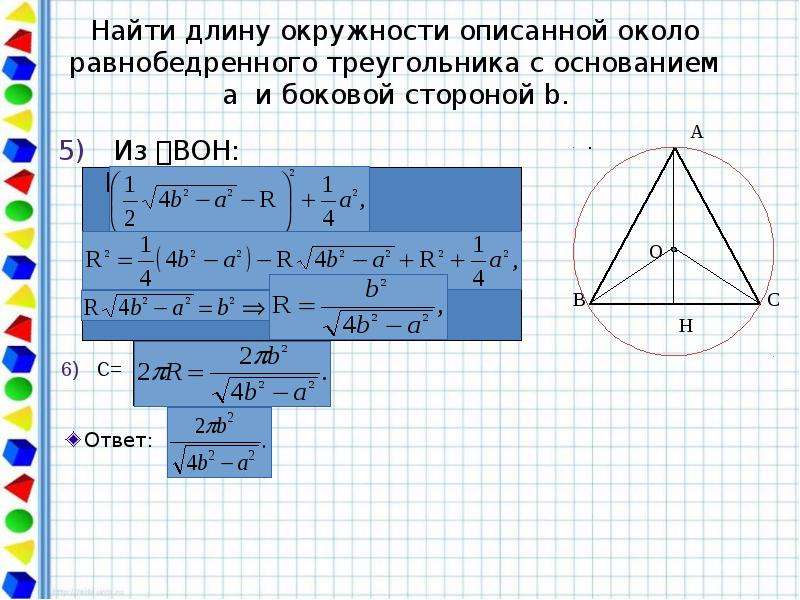
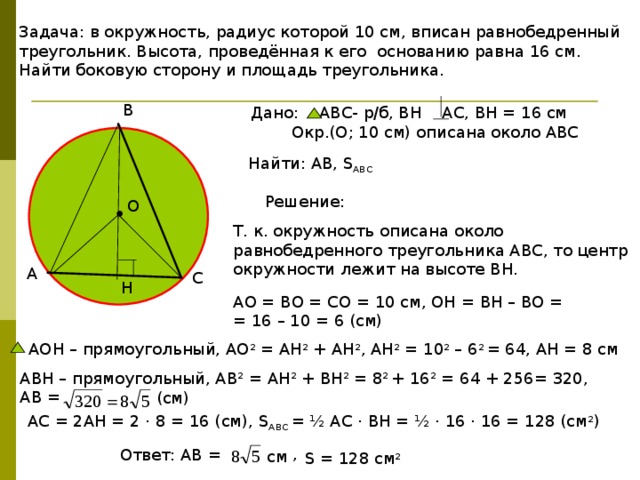
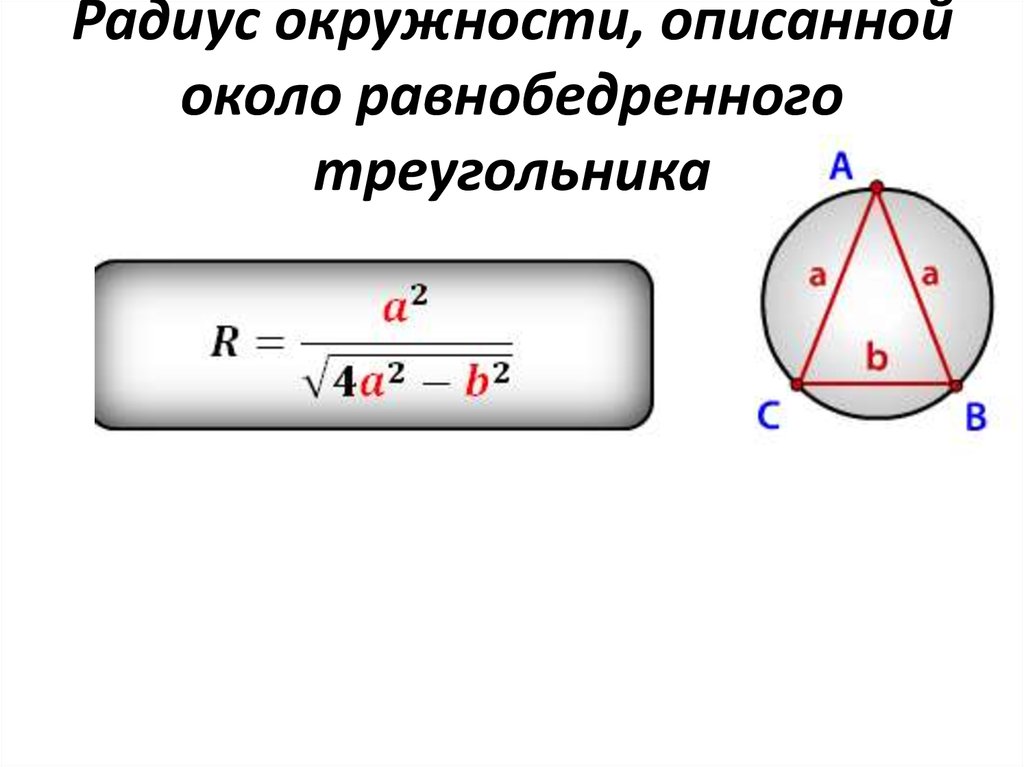
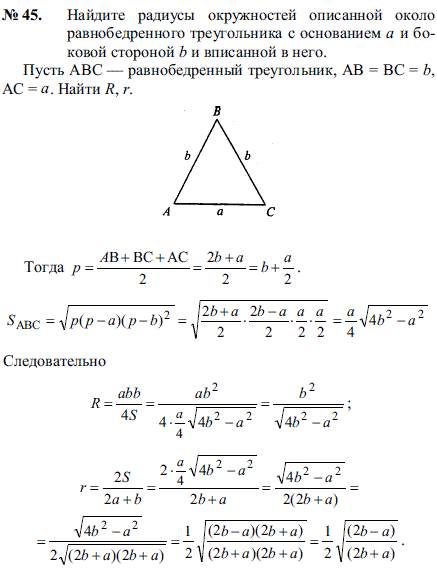Радиус описанной около равнобедренного треугольника окружности: где a — основание, b — боковая сторона, α — угол при вершине, β — угол при основании.
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
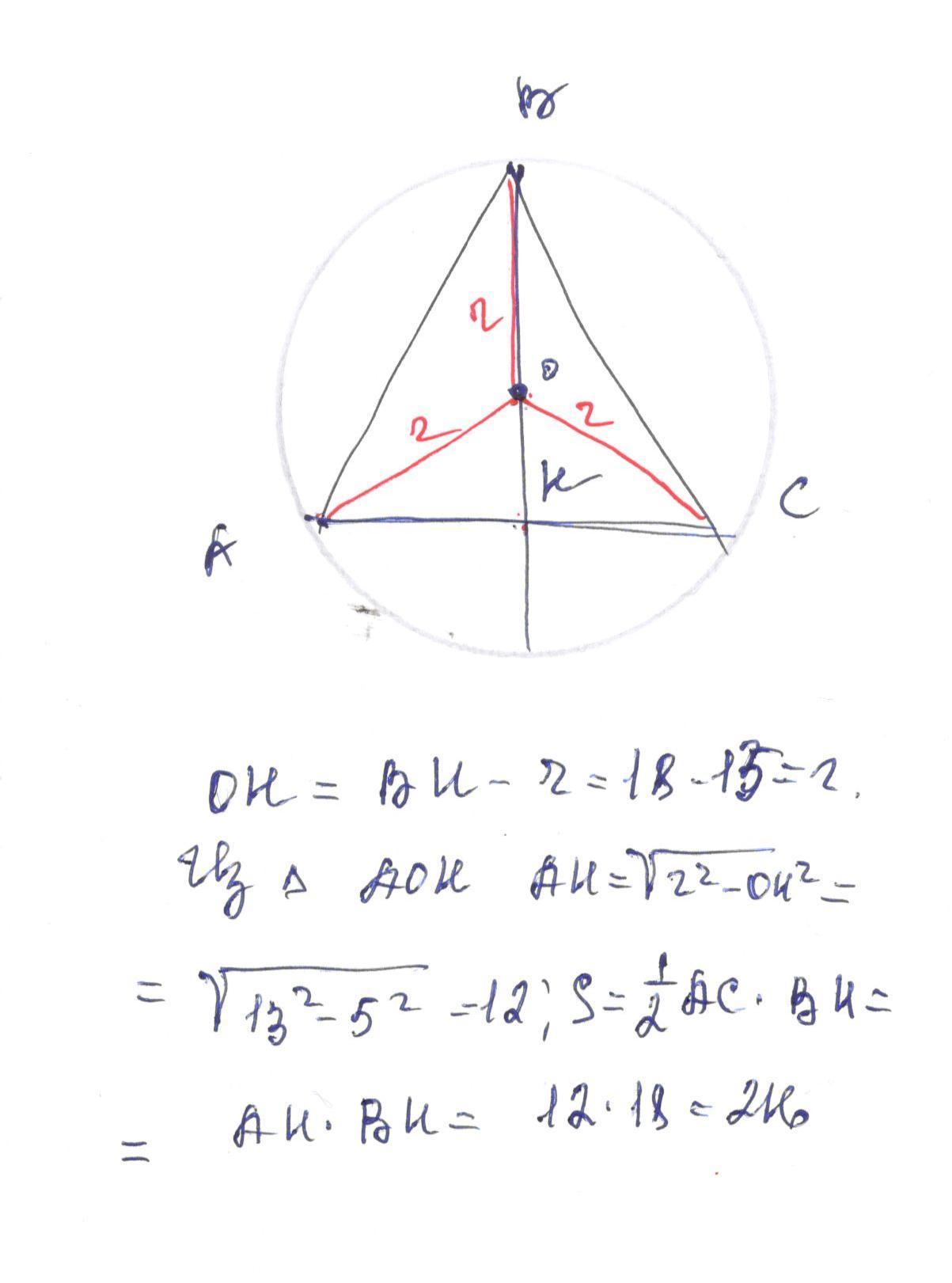
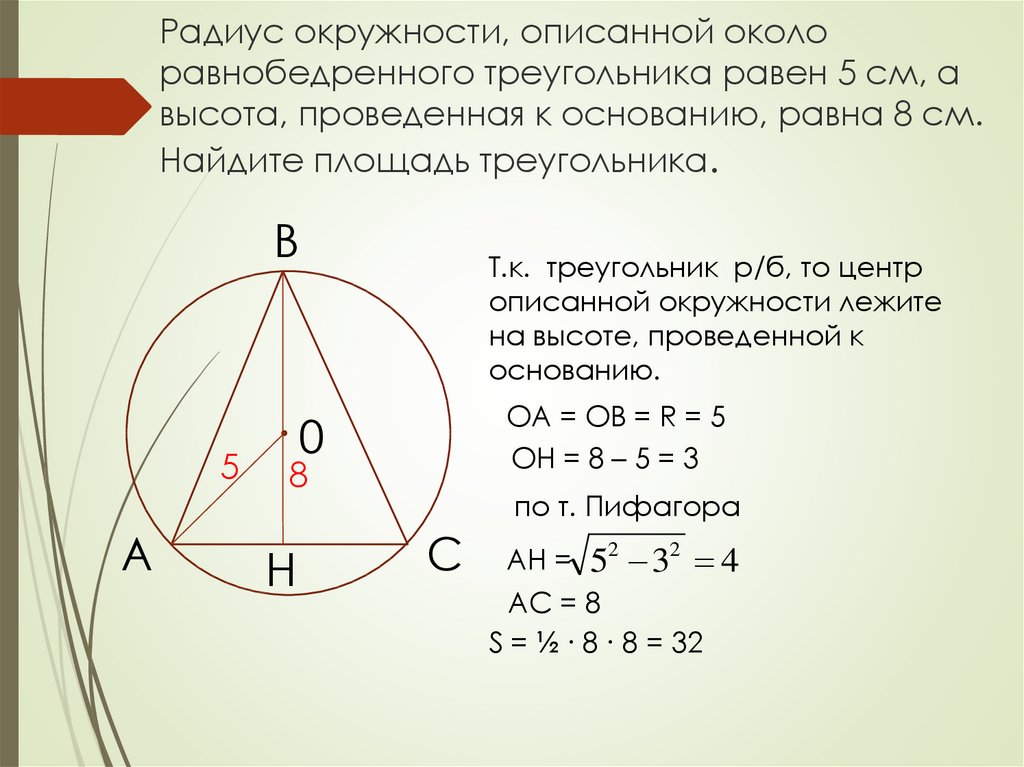
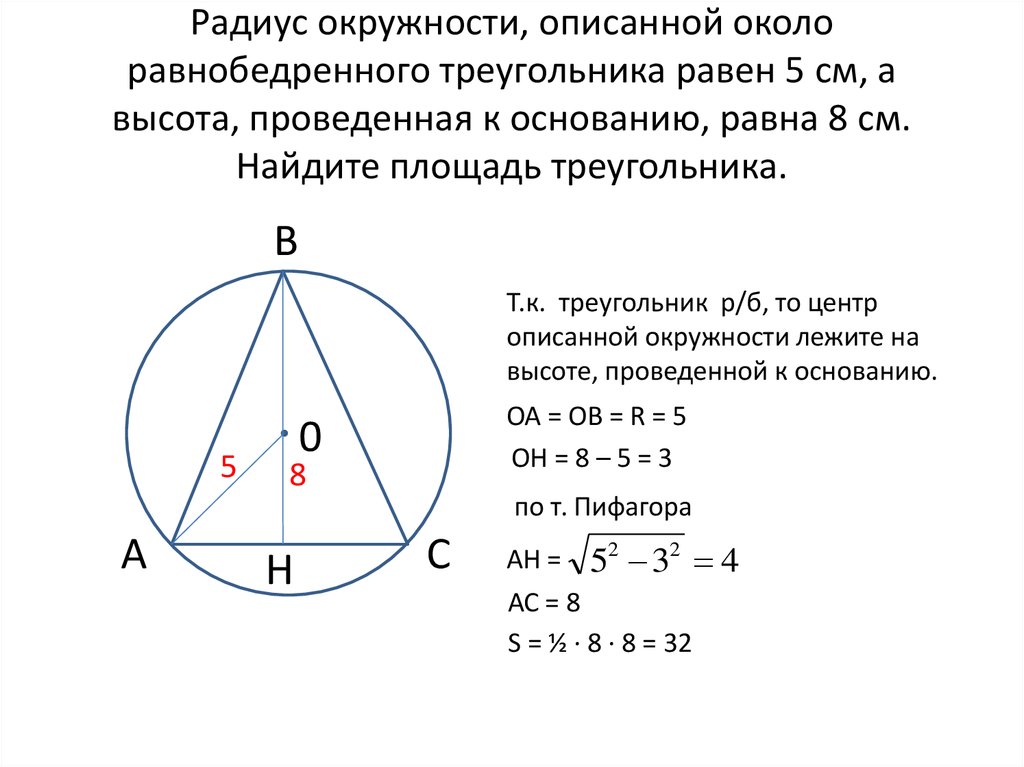В равнобедренном треугольнике АВС с основанием АС, высота bh равна половине основания ac и равна 7 см. Найти радиус описанной окружности. Ответ: радиус окружности равен 7 см.
Радиус описанной окружности равнобедренного треугольника вычисляется по классической формуле \[ R = \frac{a^2 b}{4\sqrt{p(p-a)(p-a)(p-b)}} \]
В этой статье приведены формулы для расчёта радиуса описанной около треугольника окружности для различных случаев, а именно: для прямоугольного, равнобедренного и равностороннего треугольников. …
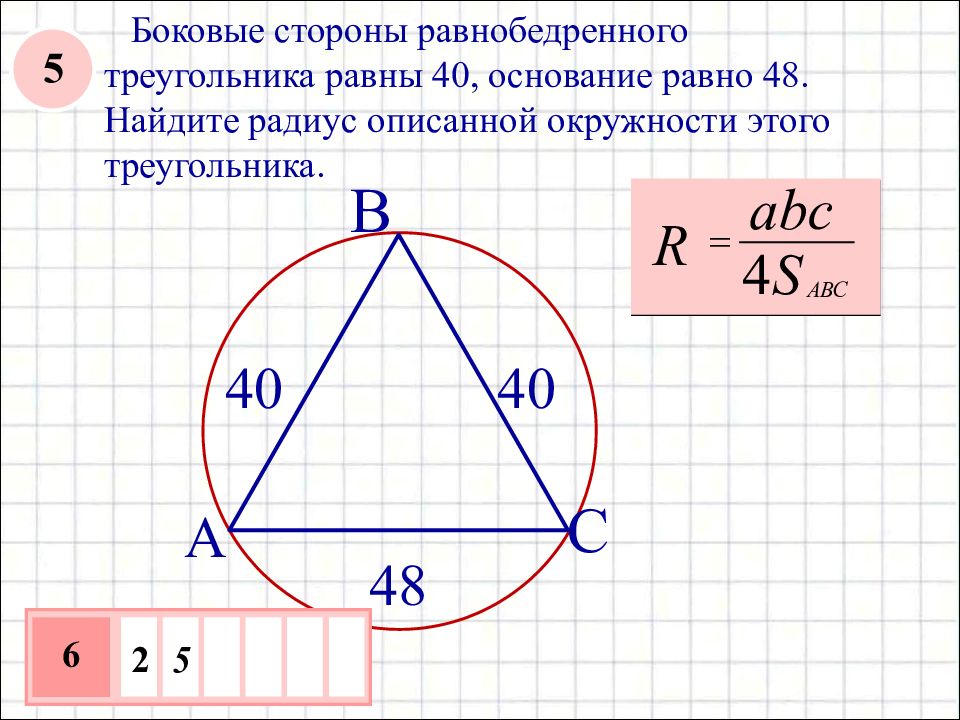Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы: Окружность, описанная около многоугольника. Если около многоугольника …
Формула для вычисления радиуса описанной вокруг равнобедренного треугольника окружности имеет следующий вид: где a,b - стороны равнобедренного треугольника. …
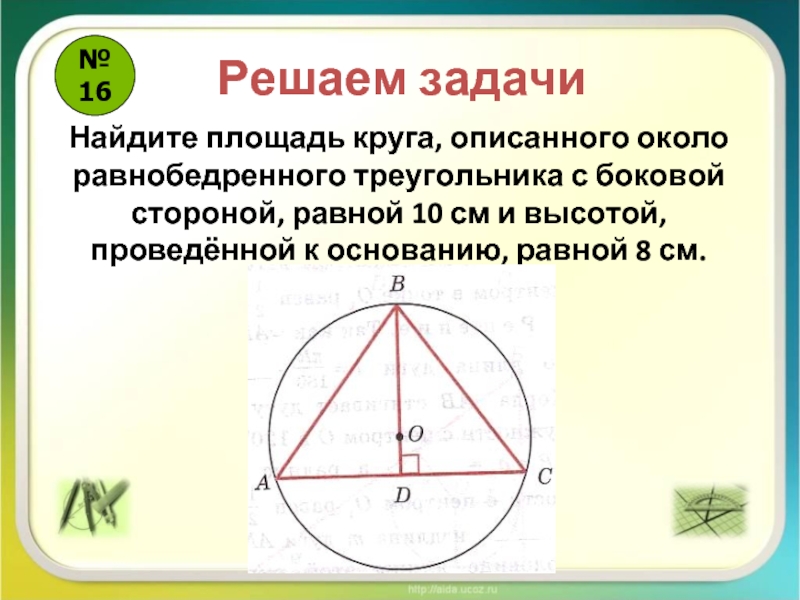
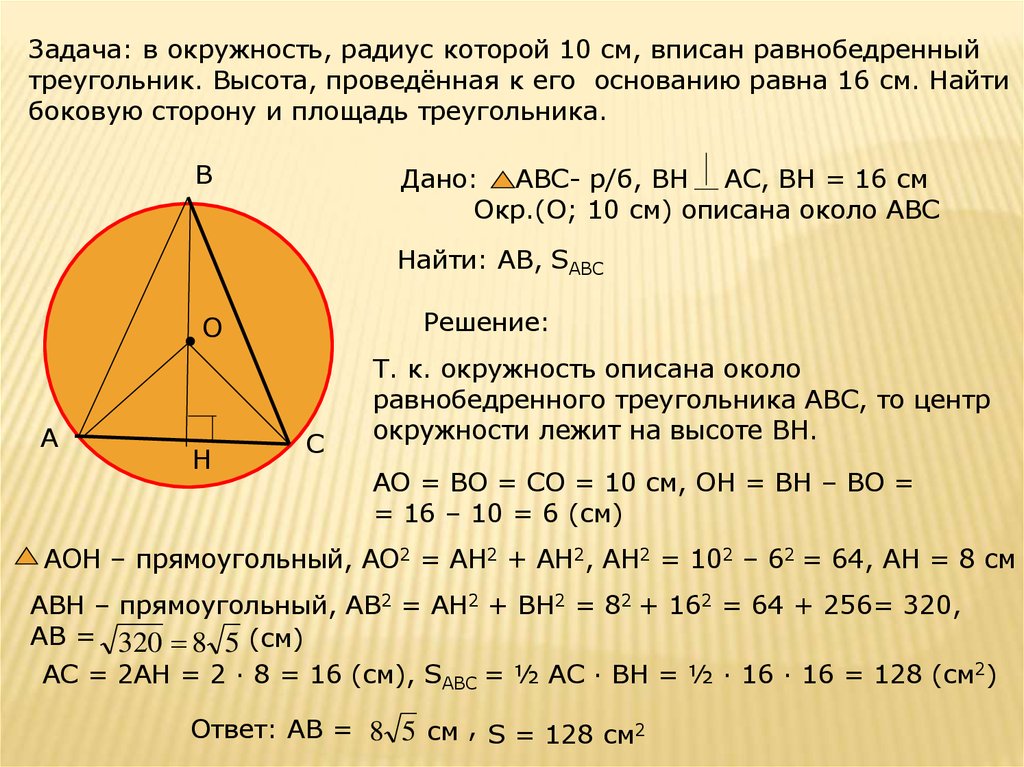
Радиус описанной окружности равнобедренного треугольника может быть найден с помощью формулы Р = (b / 2) * (√ (4 * h2 + b2) / 3), где Р — радиус описанной …
Приведены пояснения и численные примеры применения формул для расчета радиуса описанной окружности прямоугольного, равнобедренного и других видов треугольников.
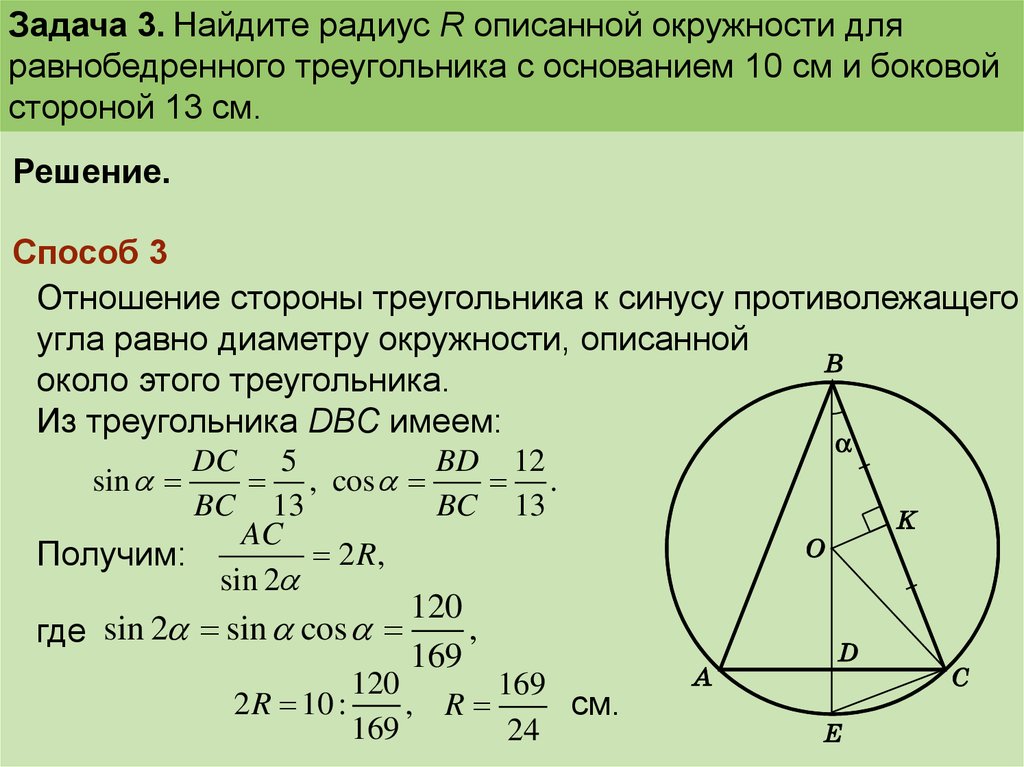
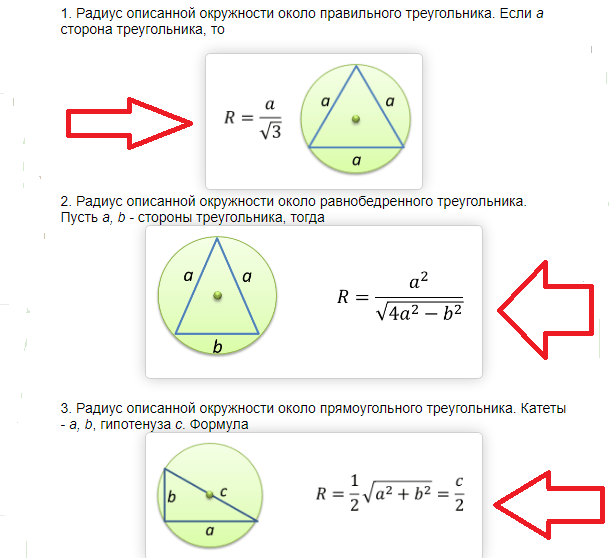Для произвольного треугольника стороны треугольника пропорциональны синусам противолежащих углов и равно диаметру окружности, описанной вокруг треугольника. Формула радиуса описанной.
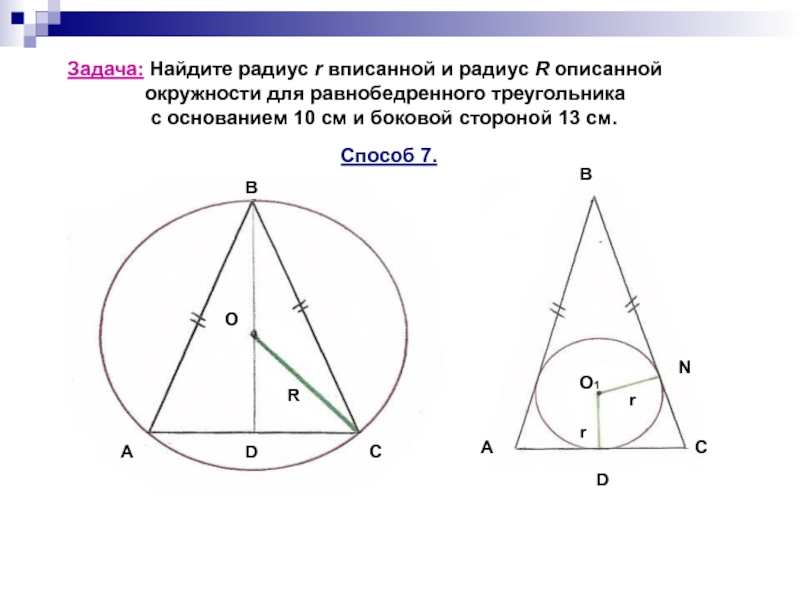Если треугольник прямоугольный, то радиус описанной окружности вычисляется по формуле: R = (a * b) / (2 * √ (a^2 + b^2)), где a и b - катеты. Рассмотрим пример.
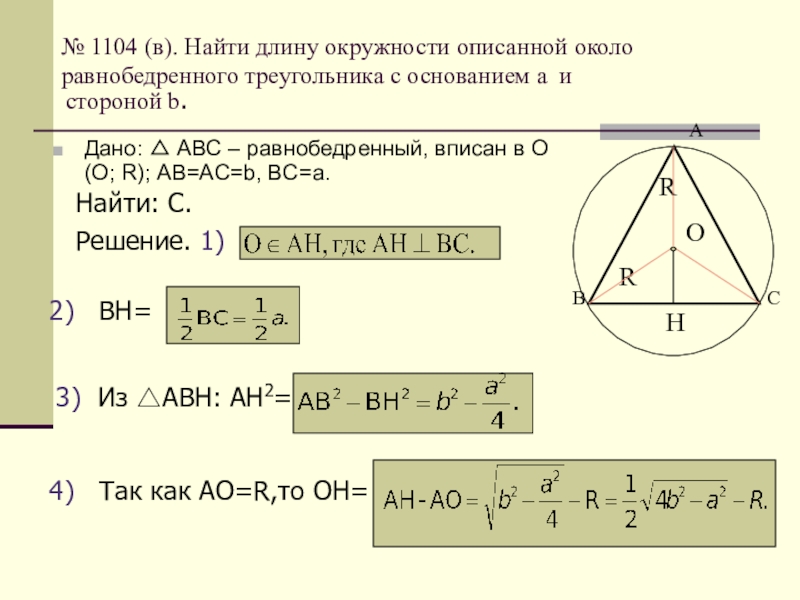
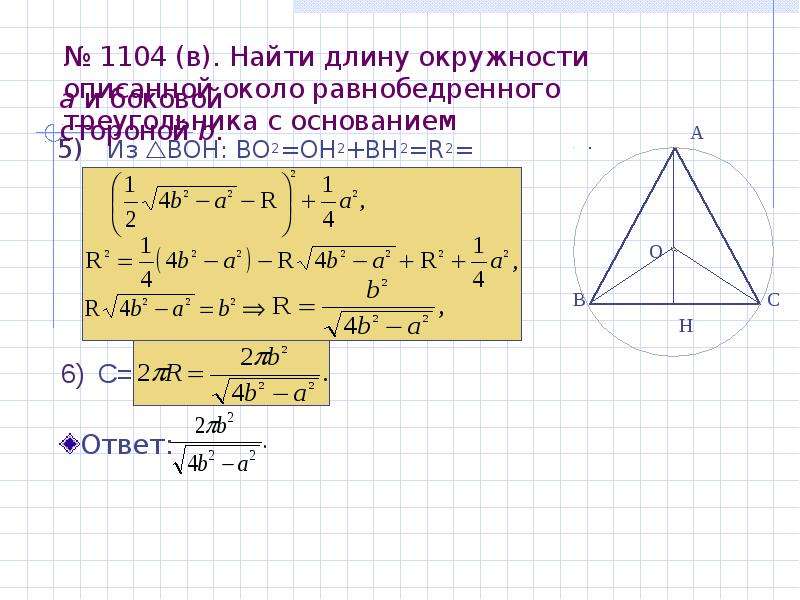
Формула нахождения радиуса описанной окружности вокруг равнобедренного треугольника по сторонам: \(R=\frac{a^2}{\sqrt{4a^2-b^2}},\) где R — радиус, a и b — стороны.
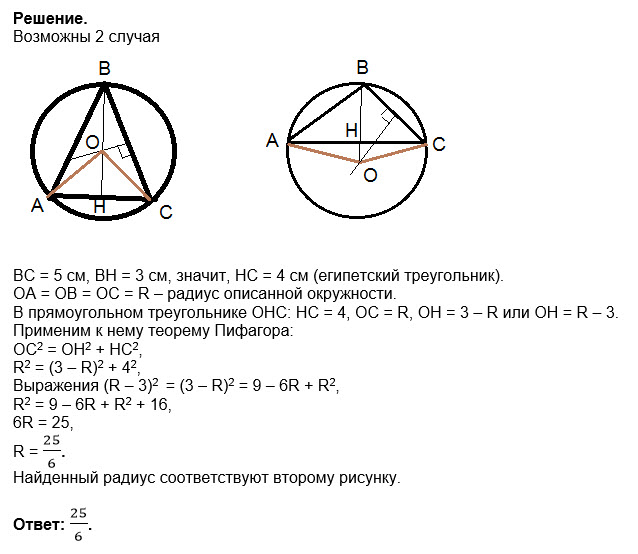
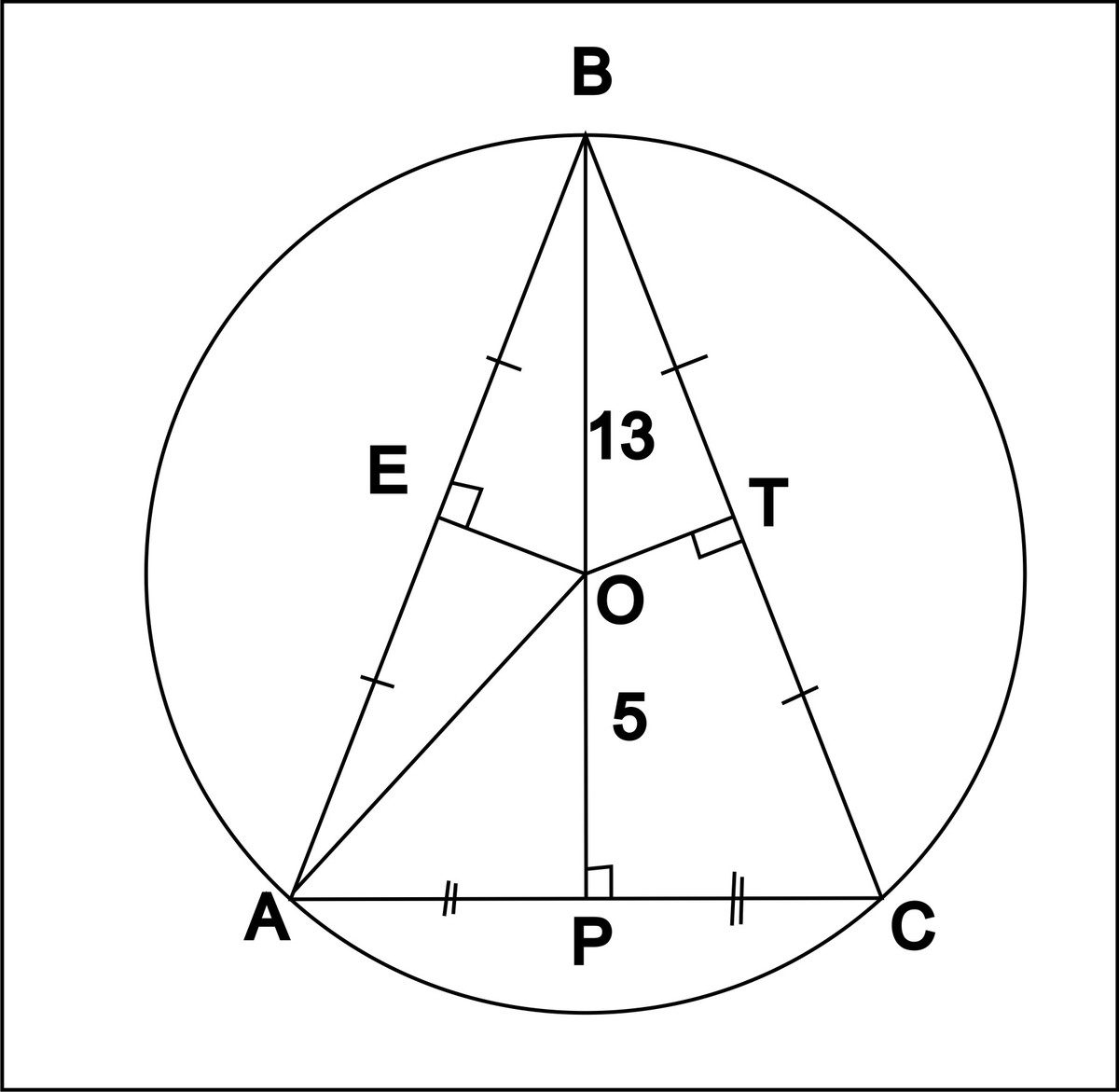В равнобедренном треугольнике АВС с основанием АС, высота bh равна половине основания ac и равна 7 см. Найти радиус описанной окружности. Ответ: радиус …
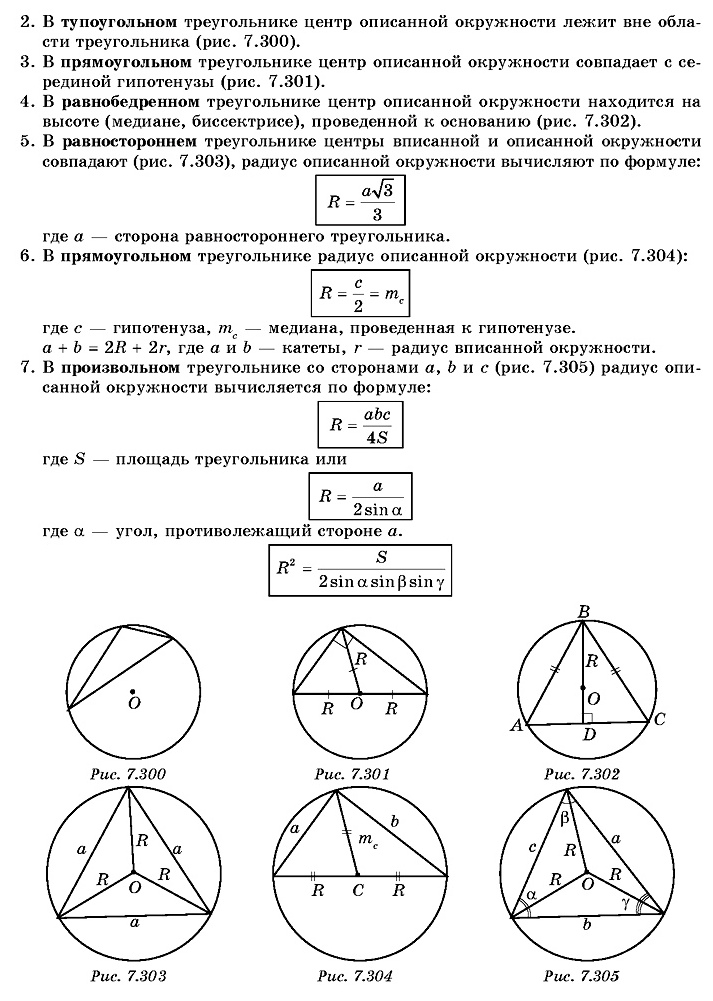Смотри также Треугольник. Вписанная окружность. Калькулятор рассчитывает радиус, площадь описанной окружности, площадь треугольника и отношение площадей.
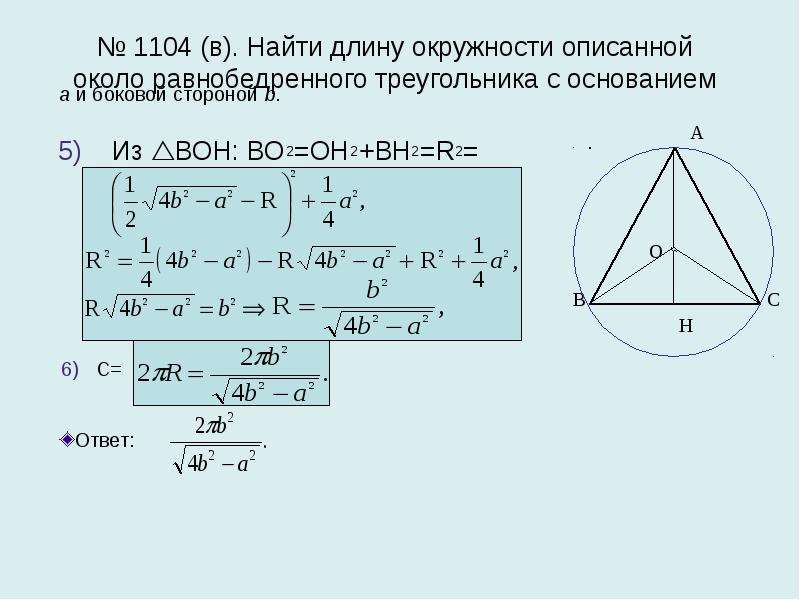Равнобедренный треугольник — треугольник, в котором две стороны имеют равную длину. Боковыми называются равные стороны, а третья сторона — основанием. Каждый …
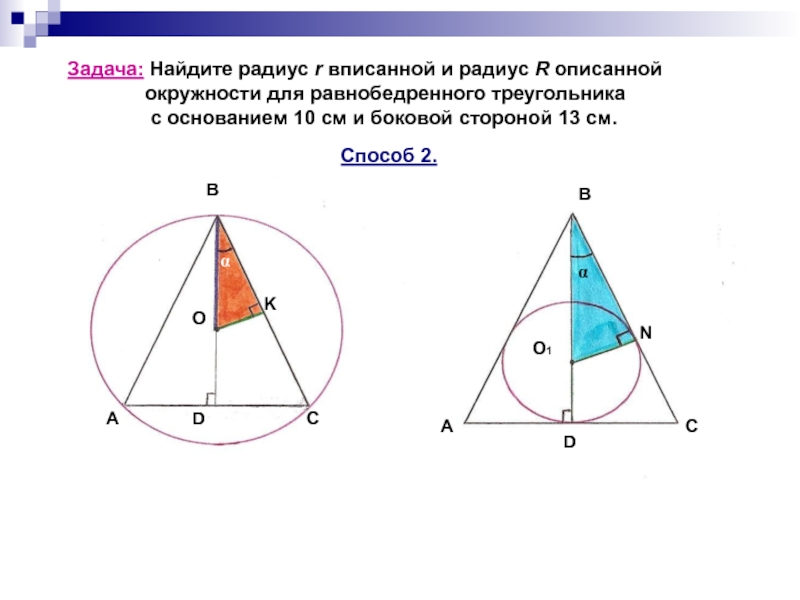Радиус вписанной окружности в треугольник (прямоугольный равнобедренный равносторонний), в квадрат, в ромб, в трапецию, в многоугольник.
Еще по теме:
Еще по теме:
