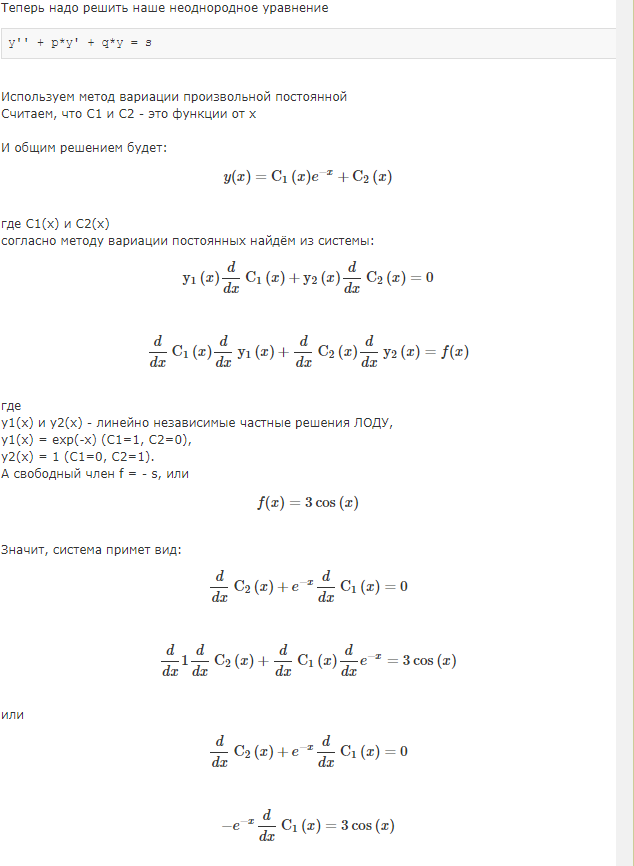Метод вариации произвольных постоянных применяется для решения неоднородных дифференциальных уравнений. Данный урок предназначен для тех студентов, кто уже …
Укажем здесь другой способ интегрирования линейных неоднородных дифференциальных уравнений, данный Лагранжем и известный под названием способа вариации …
Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных: Данное …
Для отыскания решения неоднородного уравнения так же как и в случае линейного неоднородного уравнения первого порядка, мы можем применить метод вариации …
Метод вариации произвольных постоянных. Этот метод применим к решению систем неоднородных линейных уравнений. Ограничимся для простоты нормальной …
Метод Лагранжа (метод вариации произвольных постоянных) — метод для получения общего решения неоднородного уравнения, зная общее решение однородного …
Рассмотрен метод решения линейных неоднородных дифференциальных уравнений высших порядков с постоянными коэффициентами методом вариации постоянных …
На первом этапе мы отбрасываем правую часть и решаем однородное уравнение. В результате получаем решение, содержащее n произвольных постоянных. На втором …
Для нахождения частного решения неоднородного уравнения можно пользоваться методом вариации произвольных постоянных. Он заключается в следующем. Решение уравнения …
Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
Простейшие типы обыкновенных дифференциальных уравнений. Уравнения с разделяющимися переменными. Однородные уравнения. Уравнения Бернулли, Риккати. …
Рассмотрим решение линейного дифференциального уравнения первого порядка методом Лагранжа. В методе вариации постоянной мы решаем уравнение в два этапа. На первом …
Поэтому для нахождения общего решения лнду обычно применяют метод вариации произвольных постоянных, который всегда дает возможность найти общее …
Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициент.
Решаем линейные дифференциальные уравнения первого порядка. Применяем метод вариации произвольной постоянной или метод Лагранжа решения линейных …
0:00:10 1. Решение систем с постоянными коэффициентами и произвольной правой частью 0:00:24 2. Метод вариации 0:09:36 3. Решение задачи № 850 0:36:50 4. Экспонента …
Еще по теме:
Еще по теме:
