Треугольник BCD: стороны BD и CD равны

треугольника ВДМ равна 180°. ∠ВДМ = 180° - ∠ВМД - ∠ДВМ = 180° - 90° - 38° = 52°. Ответ: градусная мера ∠ВДМ равна 52°.

Угол bdc равен 38°, и поскольку стороны bd и cd равны, то треугольник bcd является равнобедренным. Это означает, что углы bcd и cbd равны. Так как dm - медиана, то …

Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она …

В треугольнике bcd стороны bd и cd равны, dm - медиана, угол bdc равен 38°?, расположенный на этой странице сайта, относится к категории Геометрия и …

В треугольнике abc угол c равен 90 градусов, а угол a равен 70 градусам, cd БИССЕКТРИСА. Найдите углы треугольника BCD.

Шаги решения: 1. Так как медиана dm делит сторону bc пополам, то bd=cd. 2. Угол bdc равен 38 градусов. 3. В треугольнике bdc bd=cd, поэтому углы bcd и cbd равны между …

Давайте разберемся с углами в треугольнике bmd и треугольнике bdm. В треугольнике BCD стороны BD и CD равны, поэтому угол BCD равен углу CBD.

Сначала доказываешь что треугольник bdc равнобедренный, это значит что из вершины медиана равна высоте и биссиктрисе.

В треугольнике bcd стороны bd и cd равны, dm - медиана, угол bdc равен 38°. Найдите углы bmd и bdm.

Треугольники bcd и afe равны. Найдите сторону AE, если BC = 7см. EF = 14см, периметр треугольника BCD равен 29см.

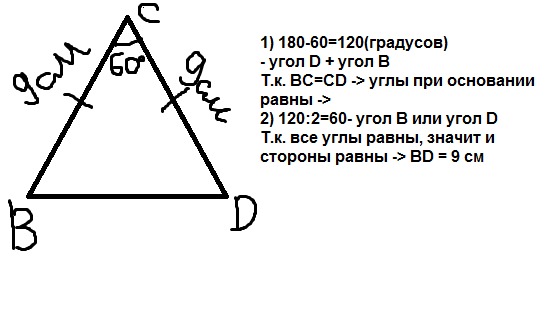
В треугольнике bcd стороны bd и cd равны, dm – медиана, угол bdc равен 38°. Найдите углы BMD и BDM. Часть 3.

bd = cd bd = dm dm = cd. Таким образом, треугольники bdm и cdm являются равнобедренными треугольниками. Это означает, что у них равны основания (стороны …

В треугольнике bcd стороны bd и cd равны, dm - медиана, угол bdc равен 38 градусов. Найдите углы BMD - ответ на этот и другие вопросы получите онлайн на сайте Uchi.ru

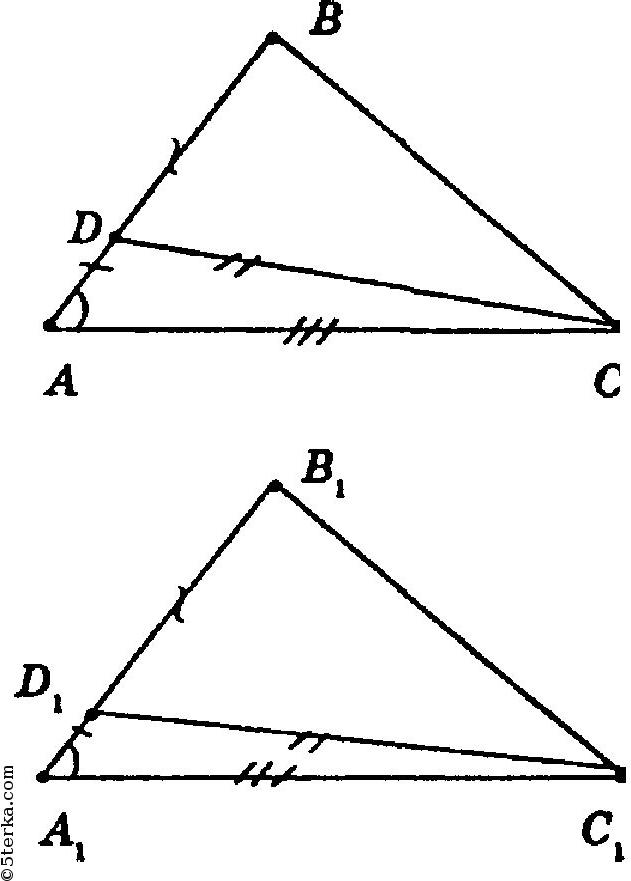
Задачи на равенство треугольников по первому признаку - сторона-угол-сторона. Задача 1. Треугольник ABC - равнобедренный, СD - биссектриса к основанию АВ. Докажите, что ACD = BCD. Доказательство.