Декартово Произведение Множеств: Определение и Примеры

Узнай, что такое декартово произведение двух множеств. Рассмотри табличное представление декартовых произведений с подробными примерами и графиками.

ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ. СООТВЕТСТВИЯ, ФУНКЦИИ, ОТНОШЕНИЯ ЦЕЛЬ ЛЕКЦИИ – изучение свойств декартова произведения множеств, и …

Декартово произведение — это умножение двух множеств, формирующее все возможные упорядоченные пары элементов исходных множеств.

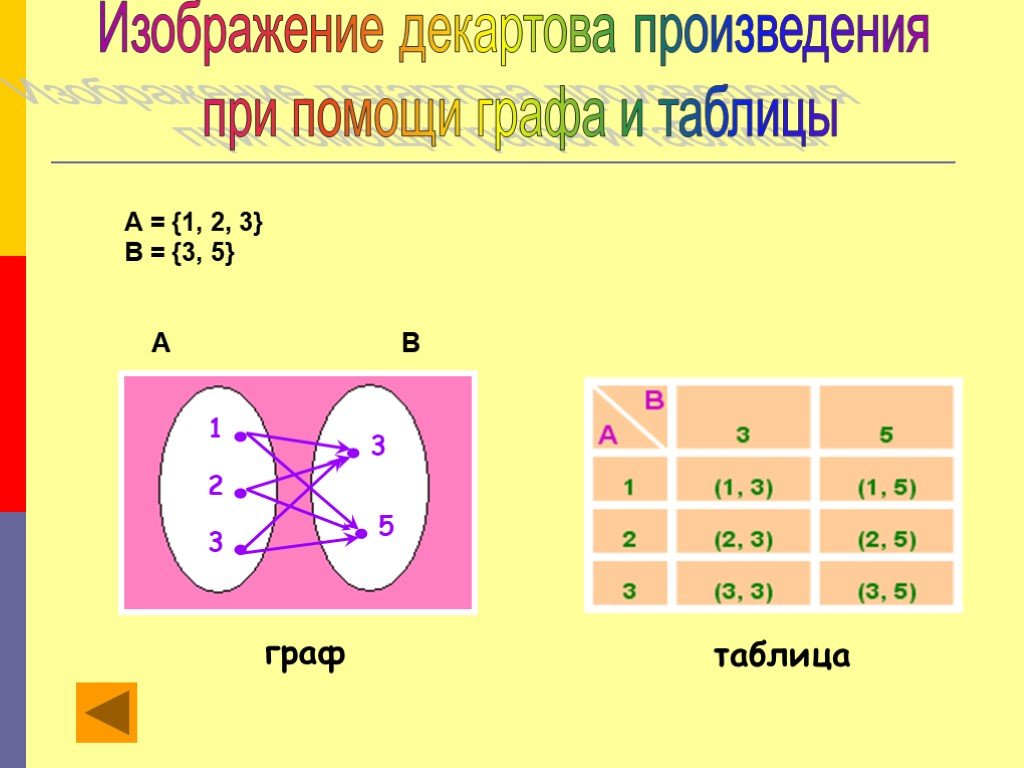
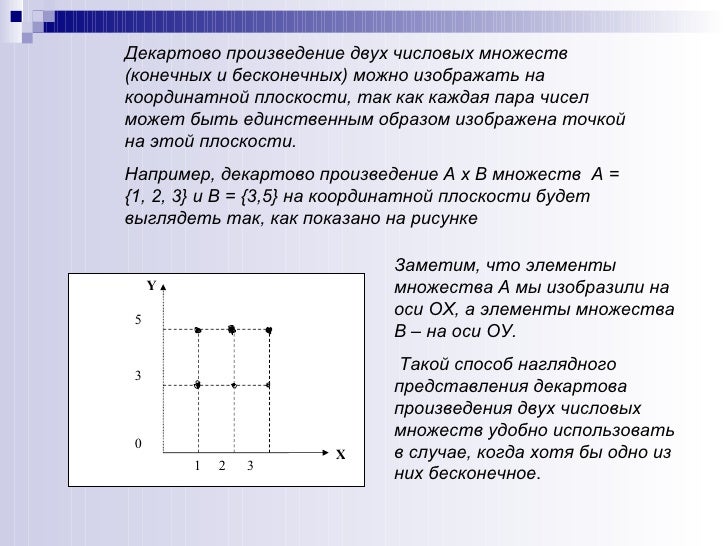
Записывают декартово произведение множеств так: A × B = { (a; b) | a ∈ A, b ∈ B}. Это значит, что если например дано множество A = {1,2,3} и множество B = {15,25}, то их …

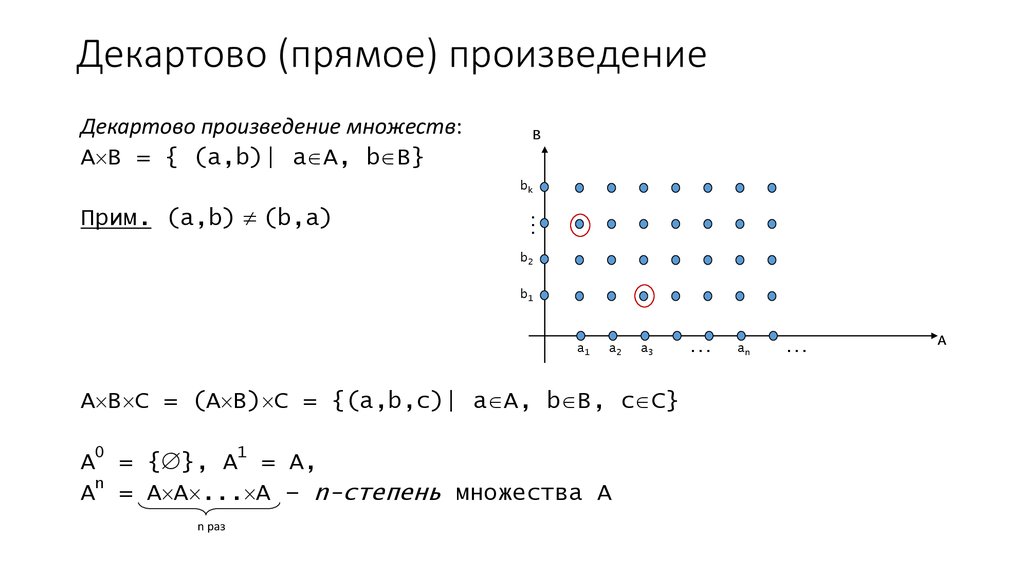
Декартовым произведением множеств A и B называется множество A х B = { (a,b)|a ∈ A,b ∈ B}. Элементами A х B являются упорядоченные пары элементов, первый — из A, второй …

Что такое произведение множеств?

Декартово произведение множеств - удивительная математическая конструкция, позволяющая комбинировать элементы разных множеств. Хотя этот термин может показаться сложным, на …

Декартово произведение множеств A и B – это множество упорядоченных пар, первый элемент которых принадлежит A, а второй – принадлежит B. Пример. …

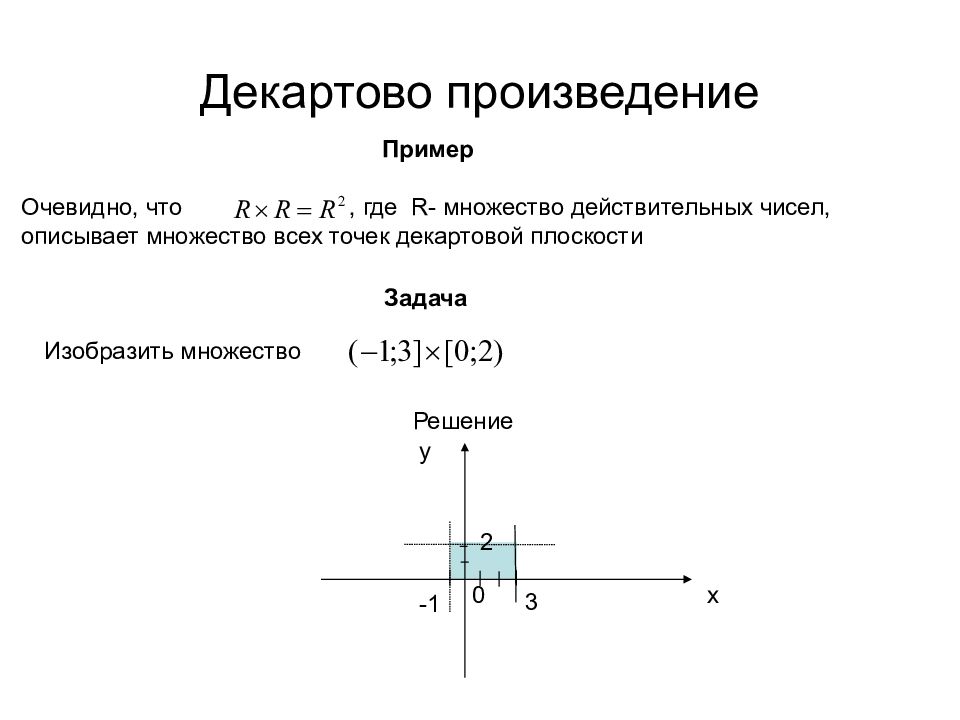
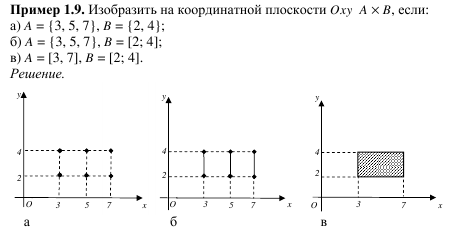
Декартово произведение множеств. Размещения с повторениями. Обобщим понятие кортежа и будем рассматривать кортежи, компоненты которых принадлежат различным …

множеств 𝐴𝐴 и 𝐵𝐵 и обозначается 𝐴𝐴× 𝐵𝐵. Перечислим некоторые простейшие свойства декартова произведения.

Кортежи и декартово произведение множеств. Определение. Пусть даны множества A 1 , A 2 ,., A n. Кортежем (или вектором) длины n, составленным из элементов этих множеств, …

Декартово произведение двух множеств обладает следующими свойствами: · A×B ≠ B×A –некоммутативность. · A× (B×С) = (A×B) ×C = A×B×C – ассоциативность. · A× (B C) = …

Декартово произведение множеств — Прямое или декартово произведение множеств множество, элементами которого являются всевозможные упорядоченные пары …

Рассмотрим несколько свойств декартова произведения множеств: 1. Если A, B — конечные множества и A n, B m, то AuB тоже конечное множество, причем A u B n m. И наоборот, …