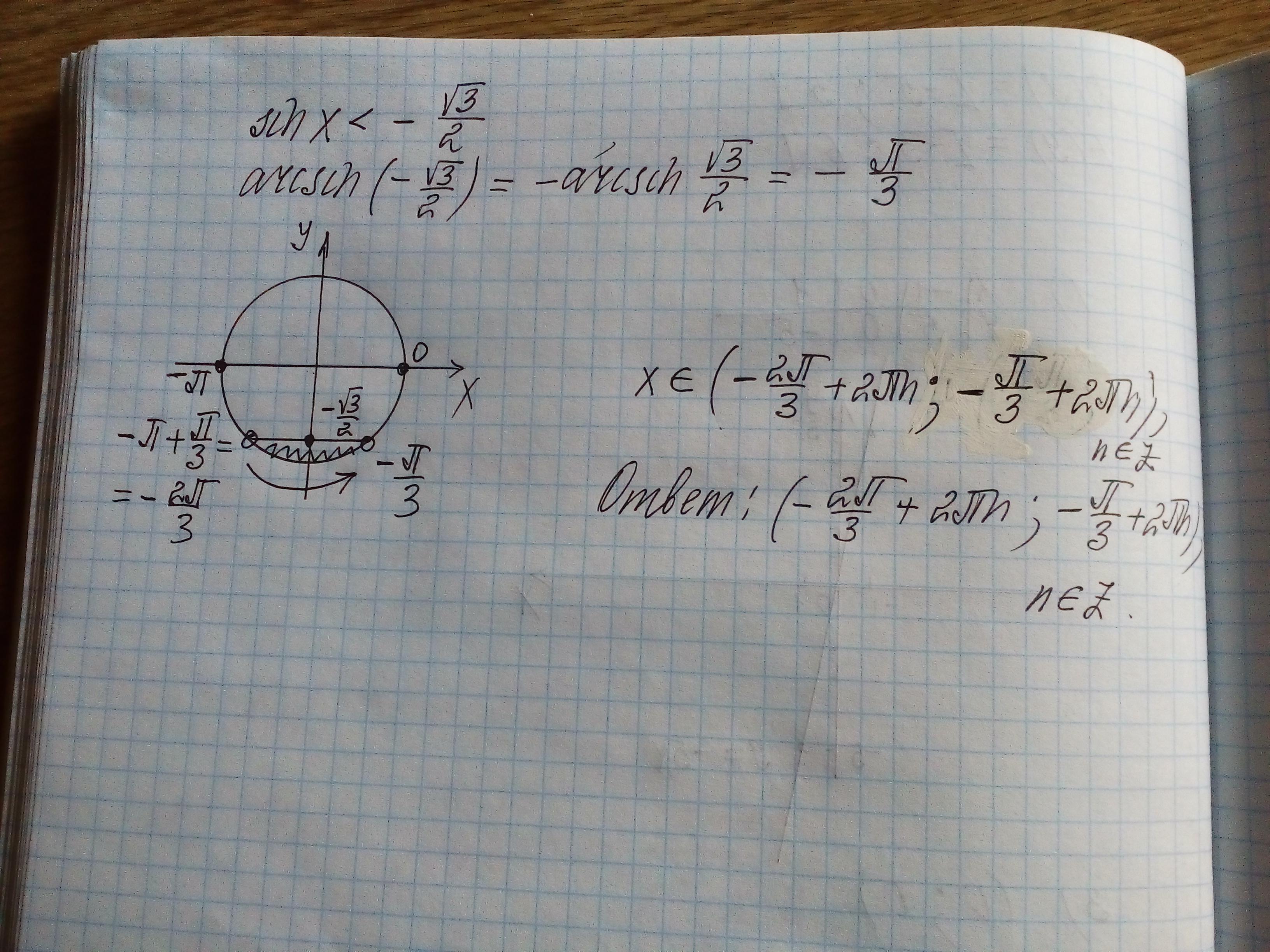Вычислить sin(x)=(( квадратный корень из 3)/2) Step 1 Возьмем обратный синус обеих частей уравнения, чтобы извлечь из синуса.
Тригонометрия. Risolvere per ? sin (x)=- ( квадратный корень из 3)/2. Этап 1. Возьмем обратный синус обеих частей уравнения, чтобы извлечь из синуса. Этап 2. Упростим правую часть. Нажмите для увеличения количества этапов. Этап 2.1. Точное значение : . Этап 3. Функция синуса отрицательна в третьем и четвертом квадрантах.
Для решения неравенства sinx>=корень 3/2 необходимо найти угол, значения синуса которого больше или равно корню из 3/2. Так как значение синуса не может быть больше 1, то можно заметить, что корень из 3/2 находится между значениями sin (pi/3) и sin (pi/2). Таким образом, решением неравенства будет любой угол x, лежащий в интервале [pi/3, …
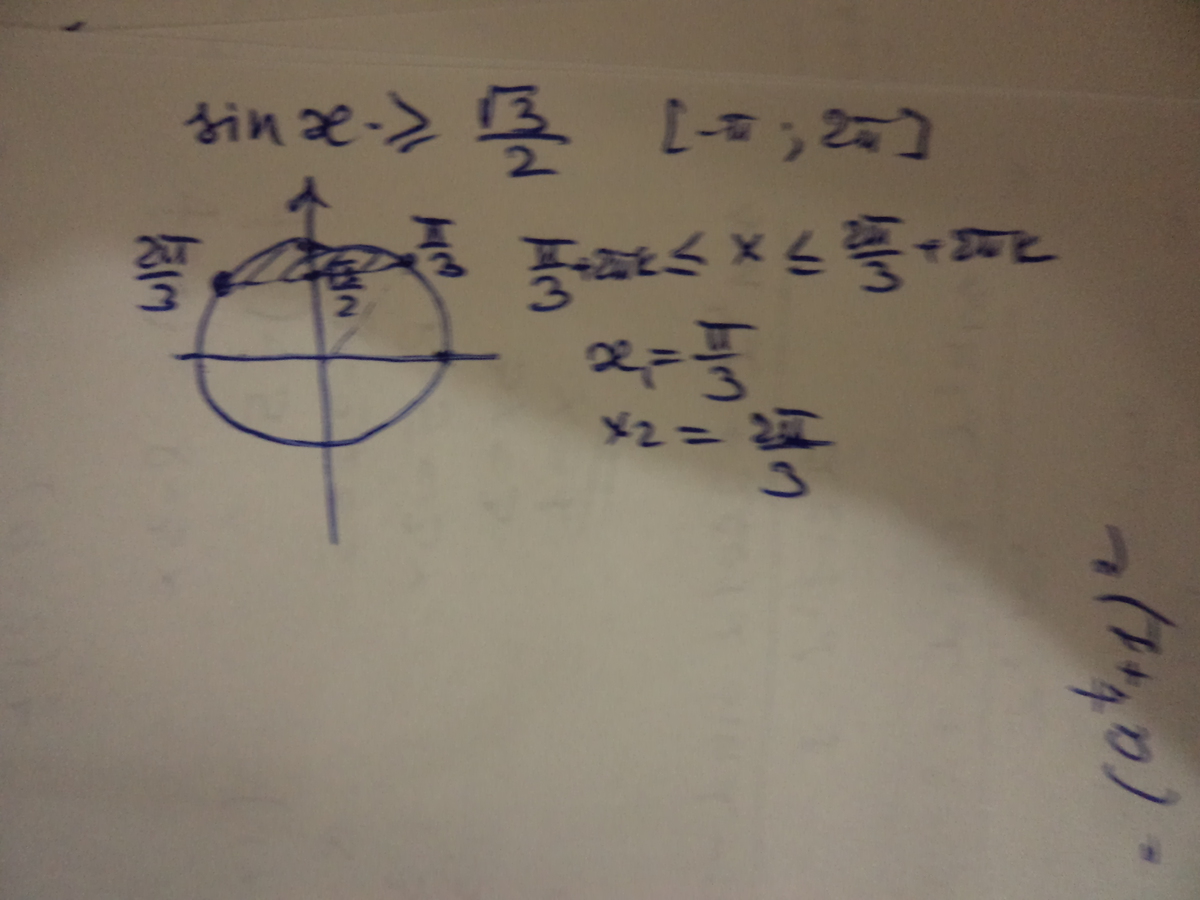Тригонометрическое уравнение sinx = корень (sqrt) из (3/2), для которого нужно найти решение. Ответ sinx=√(3/2);
sin (x) = -√3/2. Корни уравнения вида sin (x) = a определяет формула: x = arcsin (a) +- 2 * π * n, где n натуральное число. В конкретном случае: x = 2π/3 +- +- 2 * π * n. Ответ: x принадлежит {2π/3 +- +- 2 * π * n}, где n натуральное.
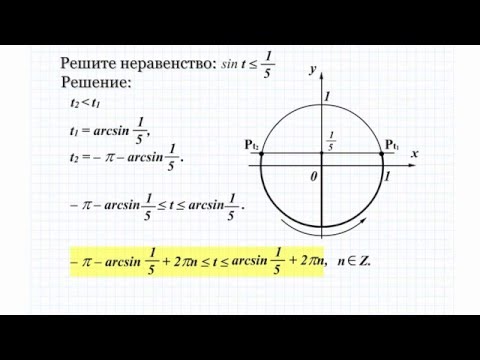
$$\sin{\left(x \right)} \leq \frac{\sqrt{3}}{2}$$ Чтобы решить это нер-во - надо сначала решить соотвествующее уравнение: $$\sin{\left(x \right)} = \frac{\sqrt{3}}{2}$$
Бесплатный корневой калькулятор - найдите корни любой функции шаг за шагом
[Есть ответ!] sin (x)=кореньиз3/2 (уравнение) Учитель очень удивится увидев твоё верное решение 😼. Примеры. Неизвестное в уравнении : Искать численное решение на промежутке: [, ] Найду корень уравнения: sin (x)=кореньиз3/2. Решение. Вы ввели [src] ___ \/ 3 . sin(x) = ----- 2 . \sin {\left (x \right)} = \frac {\sqrt {3}} {2} sin(x)= 23.
Ответы. Будь первым, кто ответит на вопрос. Sin x меньше или равно корня из 3 деленная на 2 - ответ на этот и другие вопросы получите онлайн на сайте Uchi.ru.
Бесплатное решение математических задач с поэтапными пояснениями поможет с домашними заданиями по алгебре, геометрии, тригонометрии, математическому анализу и статистике подобно репетитору по математике.
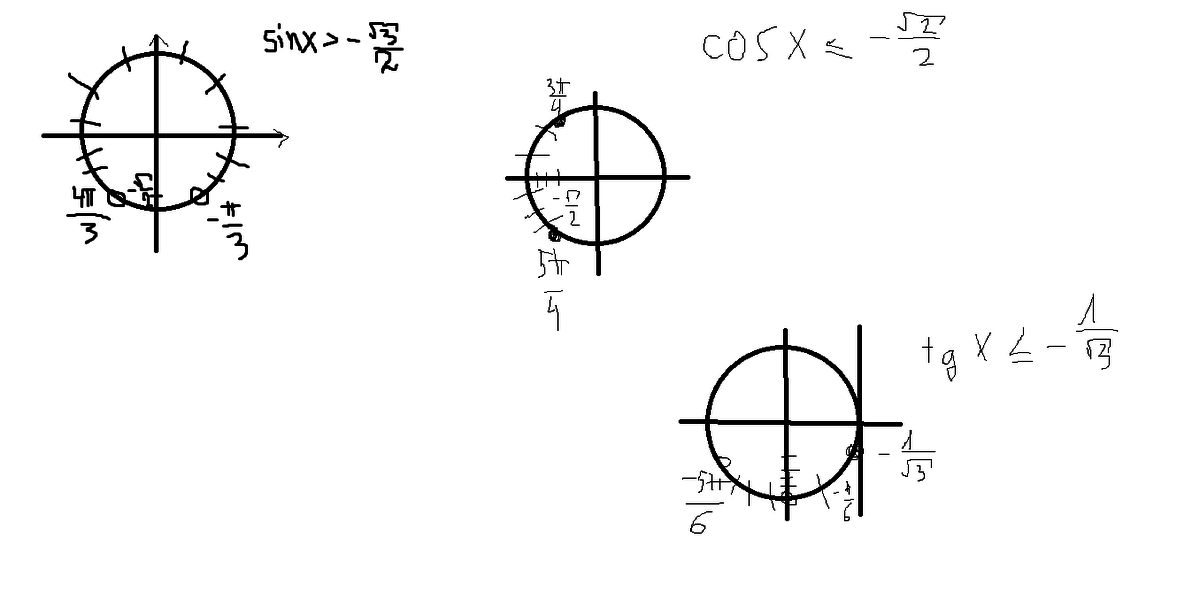Бесплатный калькулятор тригинометрических уравнений - поэтапное решение тригонометрических уравнений.
Неравенства - это выражения вида: f(x) ≥ 0. где вместо знака ≥, может стоять знак ≤ или знаки < и >. Решить приведённое выше неравенство, означает найти совокупность всех значений переменной x при которых выражение больше или равно 0. Рассмотрим график произвольной функции f(x):
Основы мат. анализа. Risolvere per x sin (x)= ( квадратный корень из 3)/2. sin(x) = √3 2 sin ( x) = 3 2. Возьмем обратный синус обеих частей уравнения, чтобы извлечь x x из синуса. x = arcsin( √3 2) x = arcsin ( 3 2) Упростим правую часть. Нажмите для увеличения количества этапов. x = π 3 x = π 3.
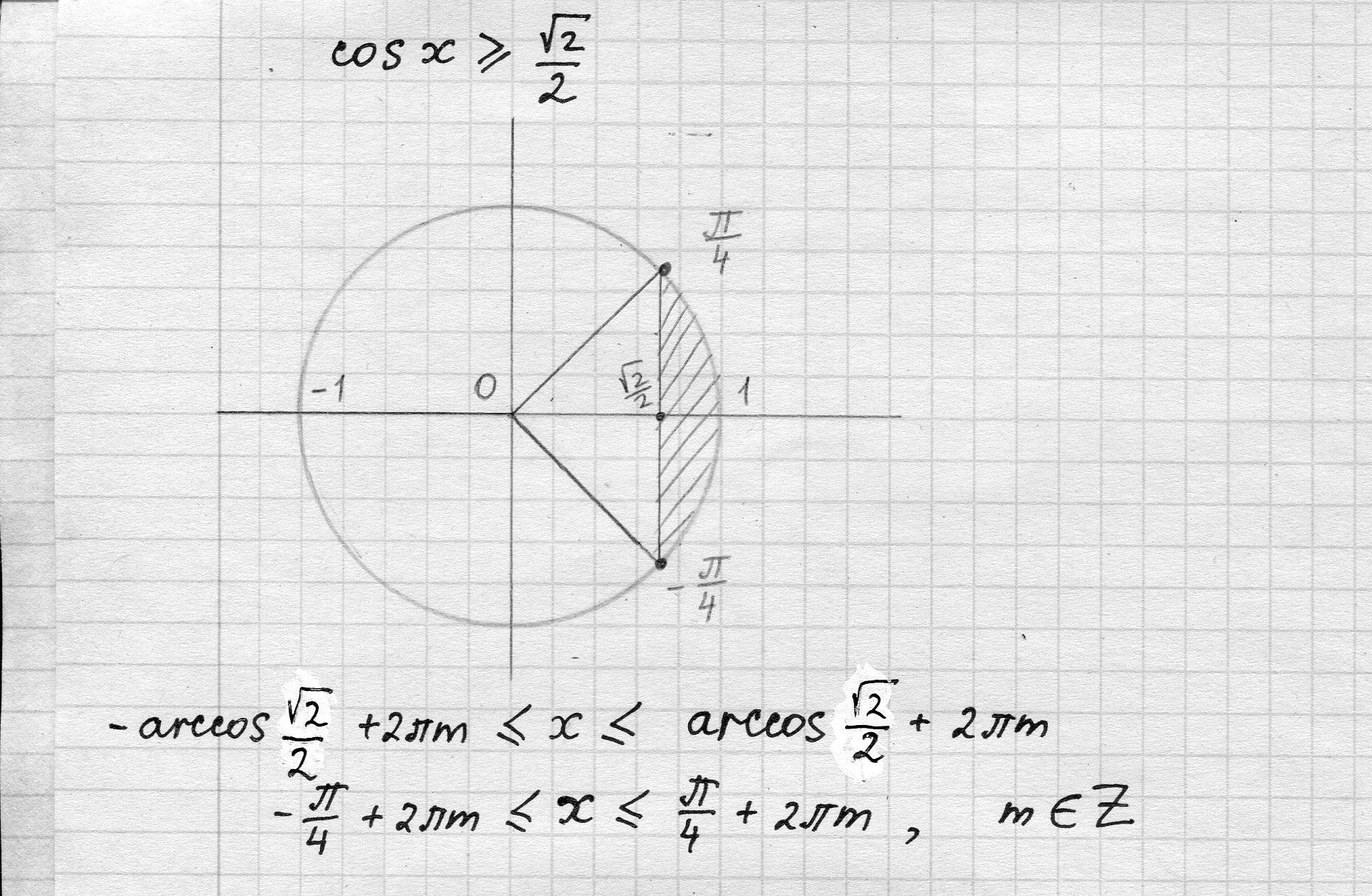
Решите неравенство sin(x)<=sqrt(2)/2 (синус от (х) меньше или равно квадратный корень из (2) делить на 2) - Укажите множество решений неравенства подробно по-шагам.
График sin (x/3)< ( квадратный корень из 3)/2. sin( x 3) < √3 2 sin ( x 3) < 3 2. Возьмем обратный синус обеих частей уравнения, чтобы извлечь x x из синуса. x 3 < arcsin( √3 2) x 3 < arcsin ( 3 2) Упростим правую часть. Нажмите.
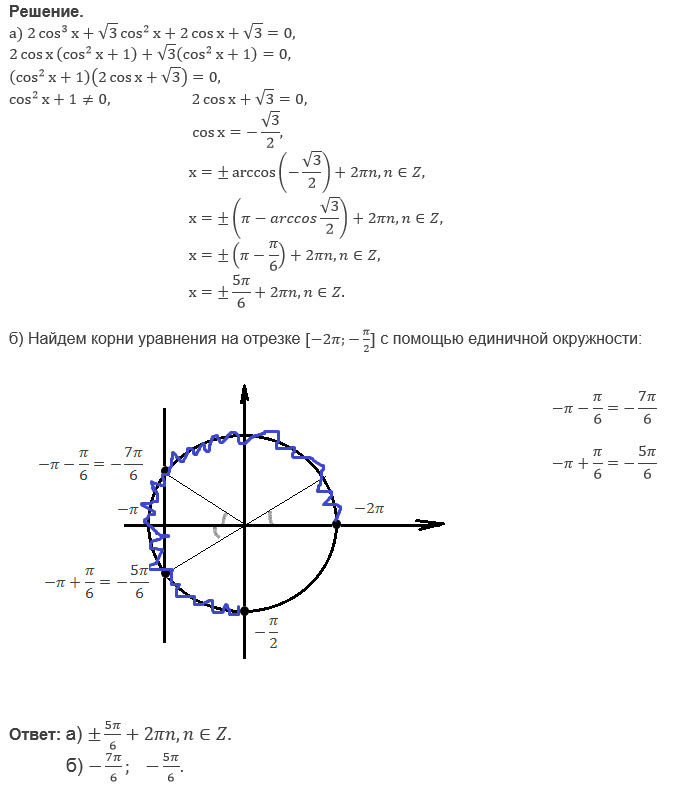
Вычисляйте тригнометрические уравнения, доказывайте тождества и вычисляйте функции шаг за шагом. сократить\:\frac {\sin^4 (x)-\cos^4 (x)} {\sin^2 (x)-\cos^2 (x)} 3\tan ^3 (A)-\tan (A)=0,\:A\in \:\left [0,\:360\right] High School Math Solutions.
Еще по теме:
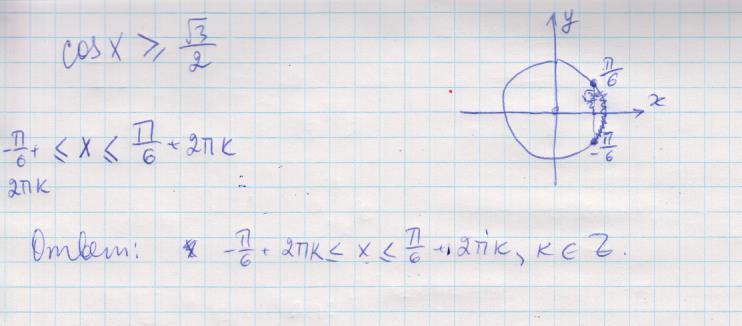
Еще по теме:
