Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O. а) …
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K, так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O. а) …
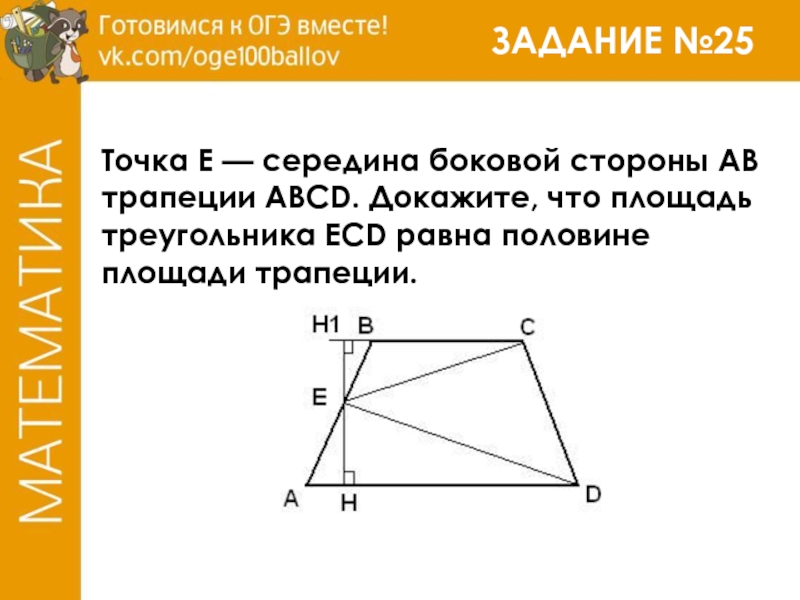
 Точка Е — середина боковой стороны АВ трапеции abcd. Докажите, что площадь треугольника ecd равна половине площади трапеции.
Точка Е — середина боковой стороны АВ трапеции abcd. Докажите, что площадь треугольника ecd равна половине площади трапеции.
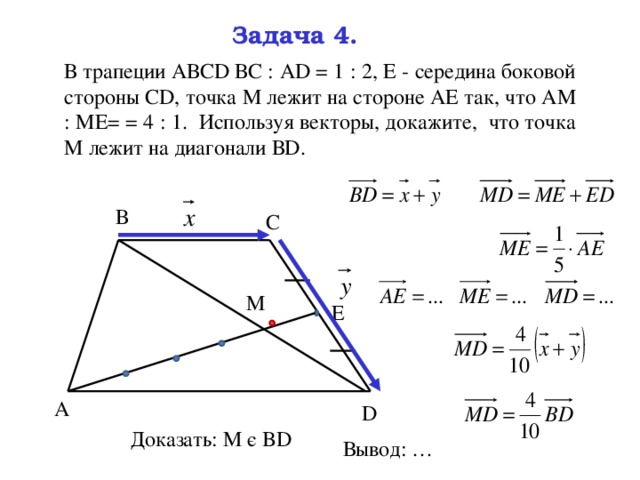
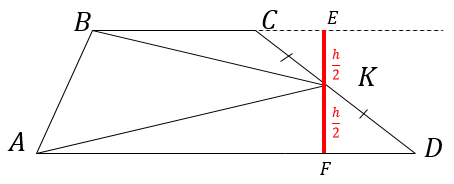
 Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции. Проведём отрезок EF параллельно основаниям трапеции, …
Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции. Проведём отрезок EF параллельно основаниям трапеции, …
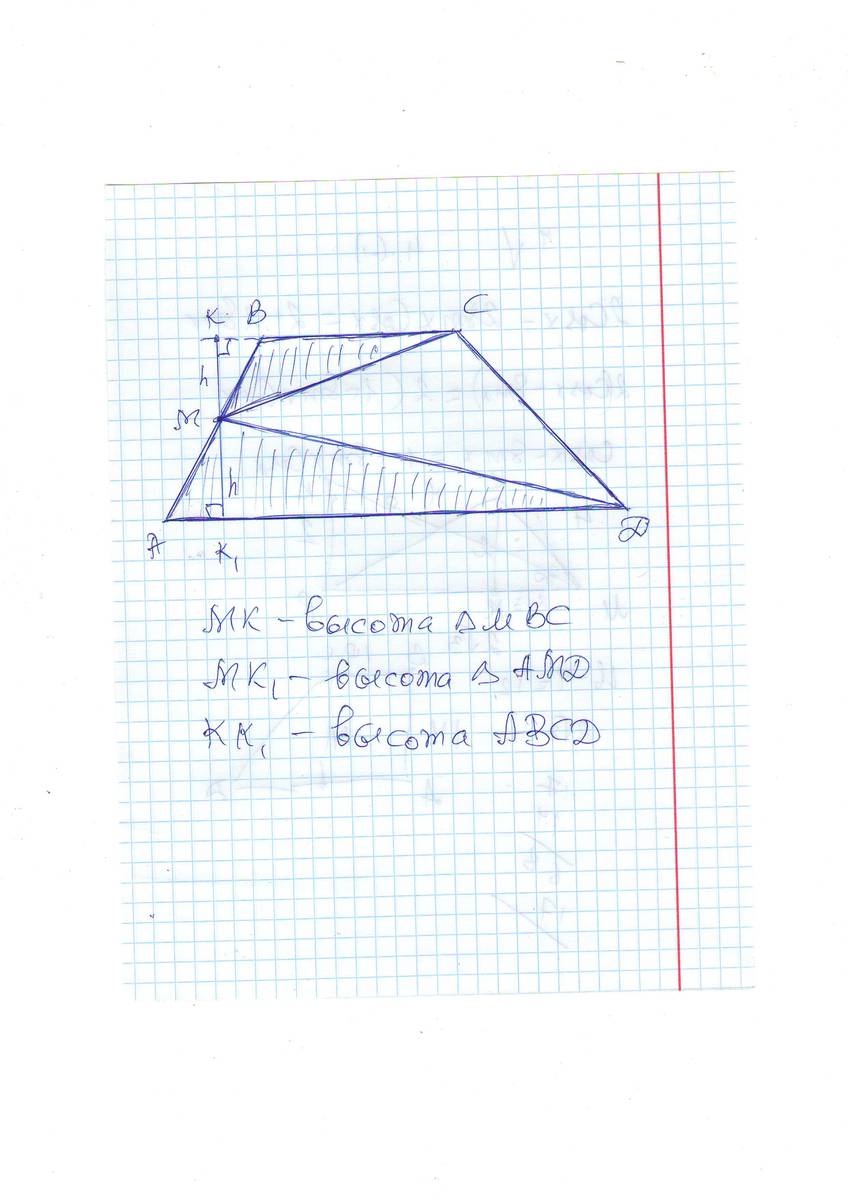
 Площадь трапеции равна произведению полусуммы оснований на высоту трапеции: Sabcd = (AB+CD)*h/2. Проведем высоту трапеции ВН (h) и среднюю линию трапеции КМ. …
Площадь трапеции равна произведению полусуммы оснований на высоту трапеции: Sabcd = (AB+CD)*h/2. Проведем высоту трапеции ВН (h) и среднюю линию трапеции КМ. …
 Докажите, что площадь треугольника равна половине площади трапеции. Показать разбор Доказательство.
Докажите, что площадь треугольника равна половине площади трапеции. Показать разбор Доказательство.
 Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB отмечена точка K так, что CK parallel AE. Отрезки CK и BE пересекаются в точке O. Докажите, что CO = …
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB отмечена точка K так, что CK parallel AE. Отрезки CK и BE пересекаются в точке O. Докажите, что CO = …
 В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей …
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей …
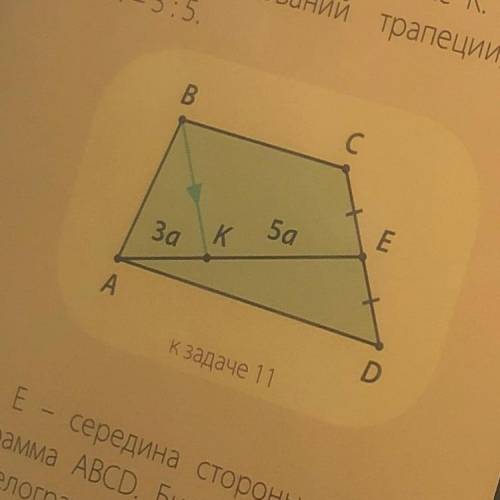
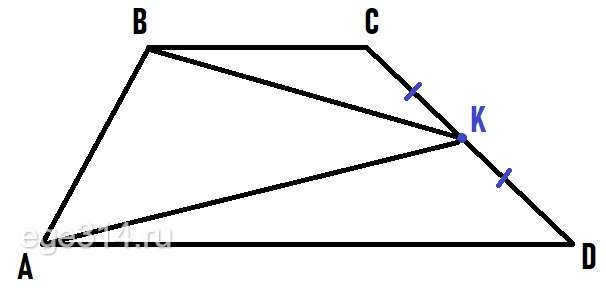
 В трапеции авсд точка к является серединой боковой стороны сд. Этот факт имеет глубокое значение в решении различных математических задач и сейчас мы с вами …
В трапеции авсд точка к является серединой боковой стороны сд. Этот факт имеет глубокое значение в решении различных математических задач и сейчас мы с вами …
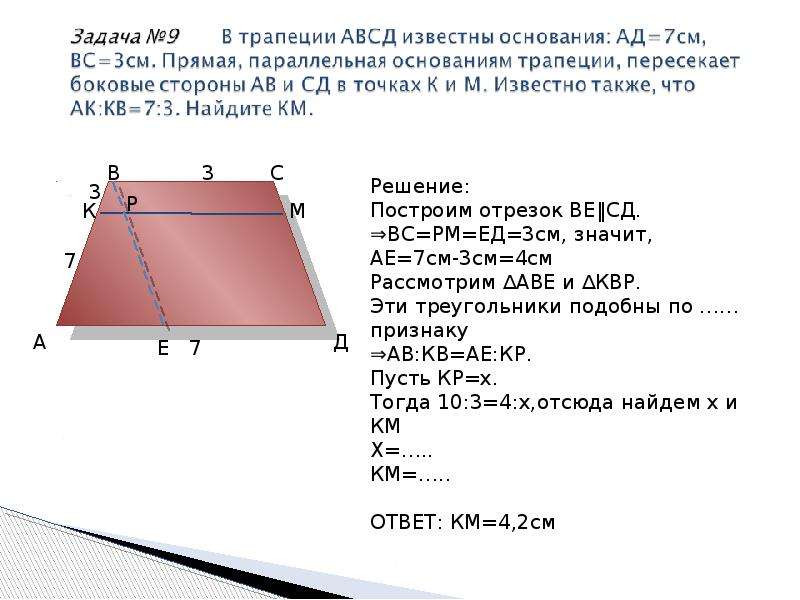
 Через точку К — середину боковой стороны CD трапеции ABCD – проведена прямая, параллельная стороне АВ и пересекающая основание AD в точке Р. Найдите отрезок …
Через точку К — середину боковой стороны CD трапеции ABCD – проведена прямая, параллельная стороне АВ и пересекающая основание AD в точке Р. Найдите отрезок …
 Так как точка Н середина СД, то прямая МН средняя линия трапеции АВСД. Построим высоту ВК, которую средняя линия делит пополам. ОВ = ОК = ВК / 2. Площадь трапеции …
Так как точка Н середина СД, то прямая МН средняя линия трапеции АВСД. Построим высоту ВК, которую средняя линия делит пополам. ОВ = ОК = ВК / 2. Площадь трапеции …
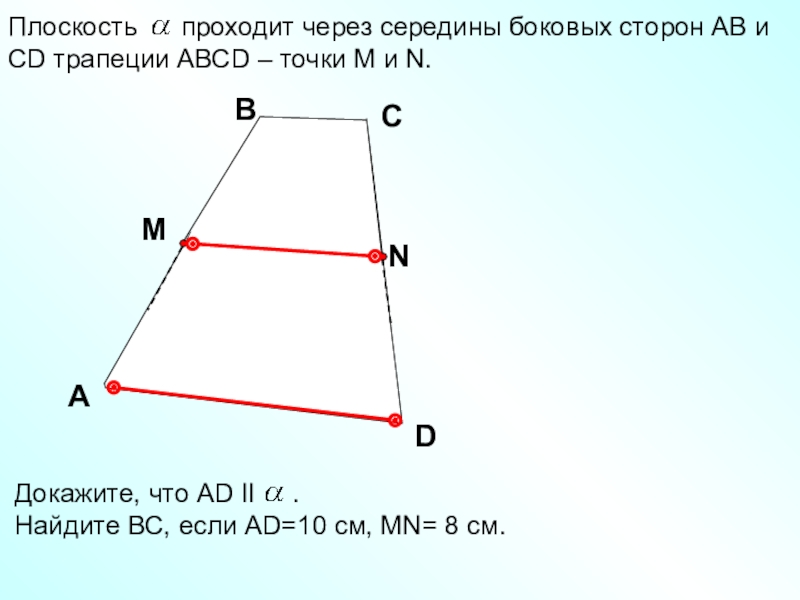
 N – середина боковой стороны, проведём среднюю линию NM трапеции АВСD: По условию NA = NB, значит ΔABN – равнобедренный. Точка M – середина AB, BM = AM, тогда NM в …
N – середина боковой стороны, проведём среднюю линию NM трапеции АВСD: По условию NA = NB, значит ΔABN – равнобедренный. Точка M – середина AB, BM = AM, тогда NM в …
 Просто потому, что точка Е - середина стороны. Так что если провести высоту трапеции, то её средняя линия, проходящая через точку Е, разобъёт эту высоты ровно пополам.
Просто потому, что точка Е - середина стороны. Так что если провести высоту трапеции, то её средняя линия, проходящая через точку Е, разобъёт эту высоты ровно пополам.
 Так как точки М и Н середины боковых сторон трапеции, то отрезок МН есть средняя линия трапеции, а следовательно МН параллельна ВС и АД.
Так как точки М и Н середины боковых сторон трапеции, то отрезок МН есть средняя линия трапеции, а следовательно МН параллельна ВС и АД.
 В трапеции, в которой боковые стороны продолжаются и пересекаются, точка пересечения делит эти стороны пропорционально (т.е., такие отрезки равны друг другу).
В трапеции, в которой боковые стороны продолжаются и пересекаются, точка пересечения делит эти стороны пропорционально (т.е., такие отрезки равны друг другу).
 Точка k — середина боковой стороны cd трапеции abcd. Докажите, что площадь треугольника ABK равна сумме площадей треугольников BCK и AKD.
Точка k — середина боковой стороны cd трапеции abcd. Докажите, что площадь треугольника ABK равна сумме площадей треугольников BCK и AKD.
 Если трапеция прямоуг-ная (АВ перп-на ВС и Аd), то: В тр-нике ABF высота, опущенная из т. F (FК) , явл-ся средней линии трапеции, отсюда:
Если трапеция прямоуг-ная (АВ перп-на ВС и Аd), то: В тр-нике ABF высота, опущенная из т. F (FК) , явл-ся средней линии трапеции, отсюда:
Еще по теме:










Еще по теме: