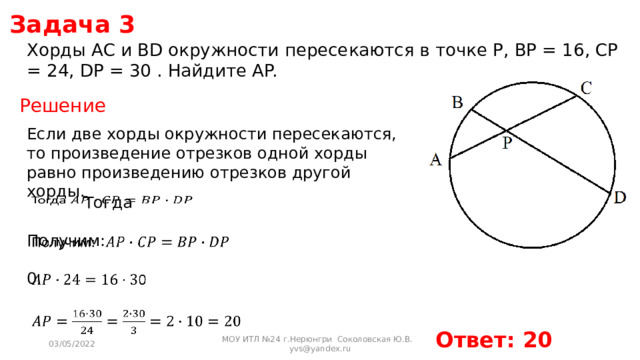
Хорды АС и bd окружности пересекаются в точке Р, bp = 9, cp = 15, dp = 20. Найдите АР.
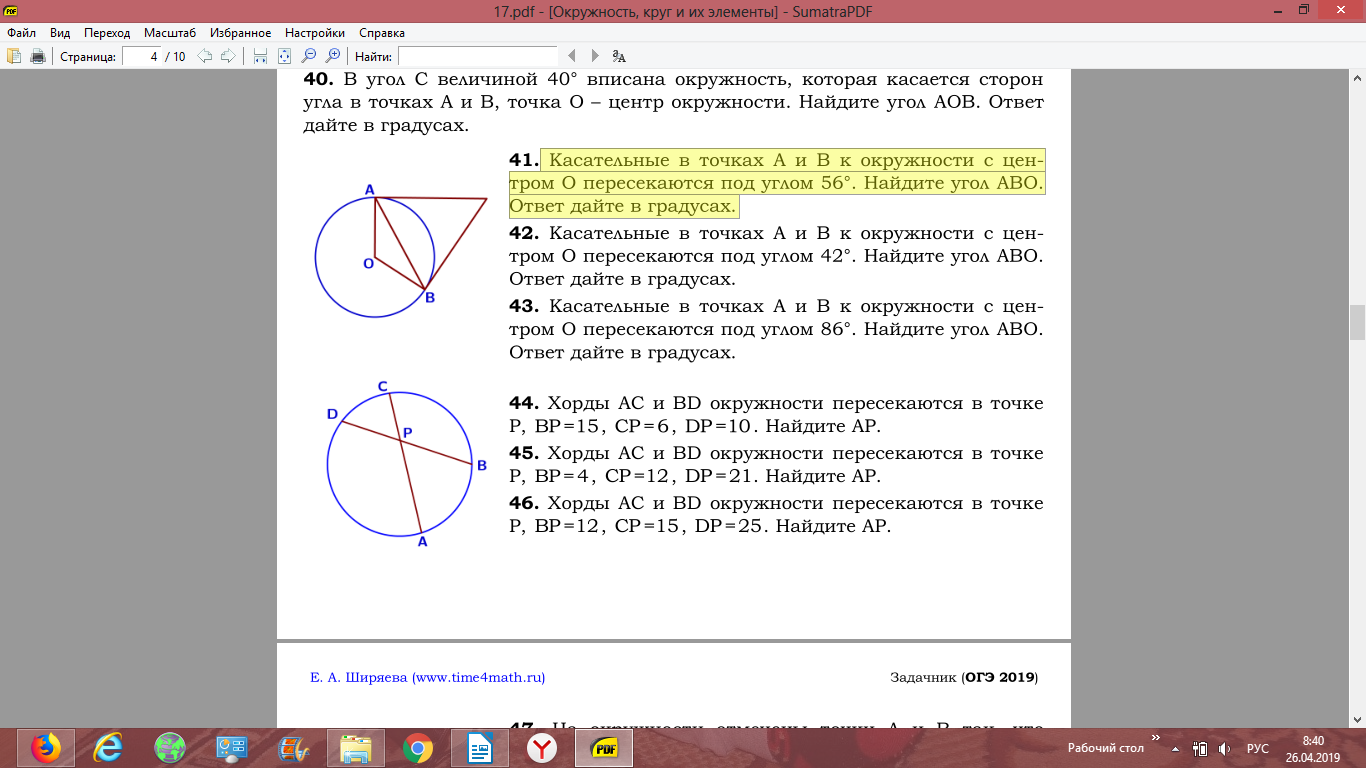
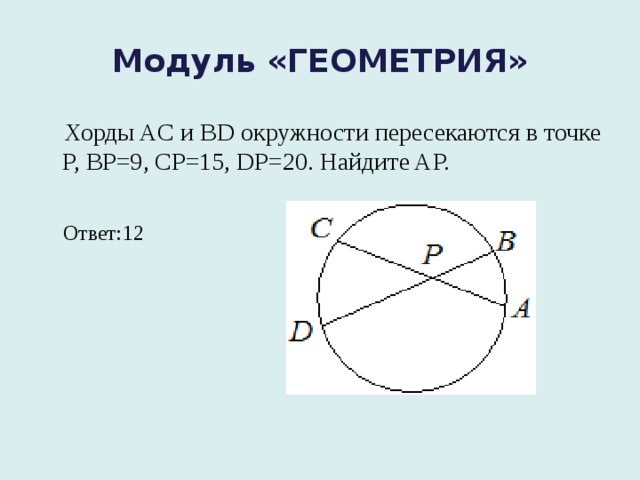Хорды ac и bd окружности пересекаются в точке p, bp = 15, cp = 6, dp = 10. Найдите AP . Спрятать решение
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 12, СР = 6, DР = 13. Найдите АР. РЕШЕНИЕ: Проведем отрезки АD и СВ. Δ АРD подобен Δ СРВ по 2-м углам. ∠ АРD = …
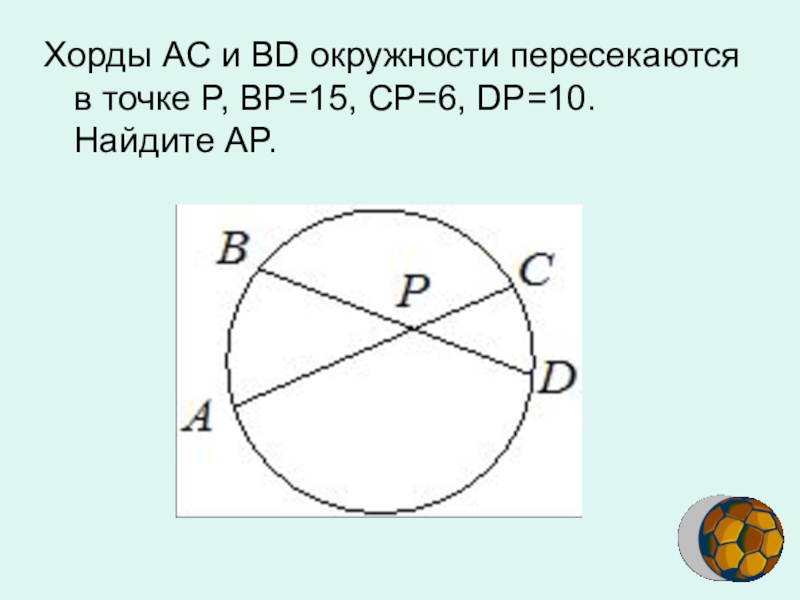Хорды АС и bd окружности пересекаются в точке Р. Перпендикуляры к АС и bd ,в точках С и d соответственно, пересекаются в точке q. Докажите, что прямые АВ и pq …
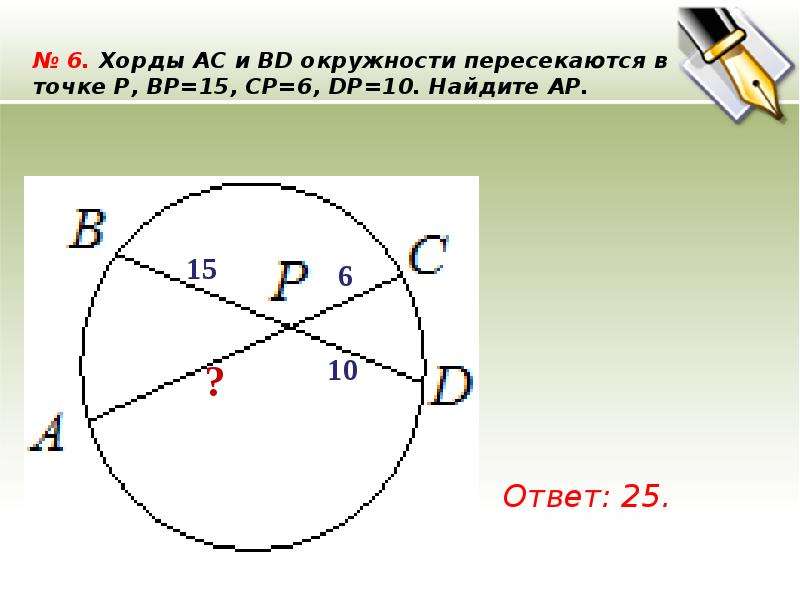Хорды ac и bd окружности пересекаются в точке p, bp=10, cp=14, dp=21. Найдите ap. Решение: Отрезки хорд относительно точки пересечения Р и по свойству хорд: bp * dp = ap * pc, отсюда АР = bp*dp pc
Хорды АС и bd пересекаются в точке Т. На хорде ВС отложен отрезок СР , равный AD . Точки Р и D равноудалены от хорды АС , а отрезок ТР перпендикулярен хорде ВС.
Теорема о произведении отрезков хорд описывает соотношения отрезков, образованных двумя пересекающимися хордами окружности. В теореме утверждается, что …
Вариант 1. Хорды АС и ВД окружности пересекаются в точке Р, ВР=10, СР=14, ДР=21. Найти АР. Через точку А, лежащую вне окружности, проведены две прямые. …
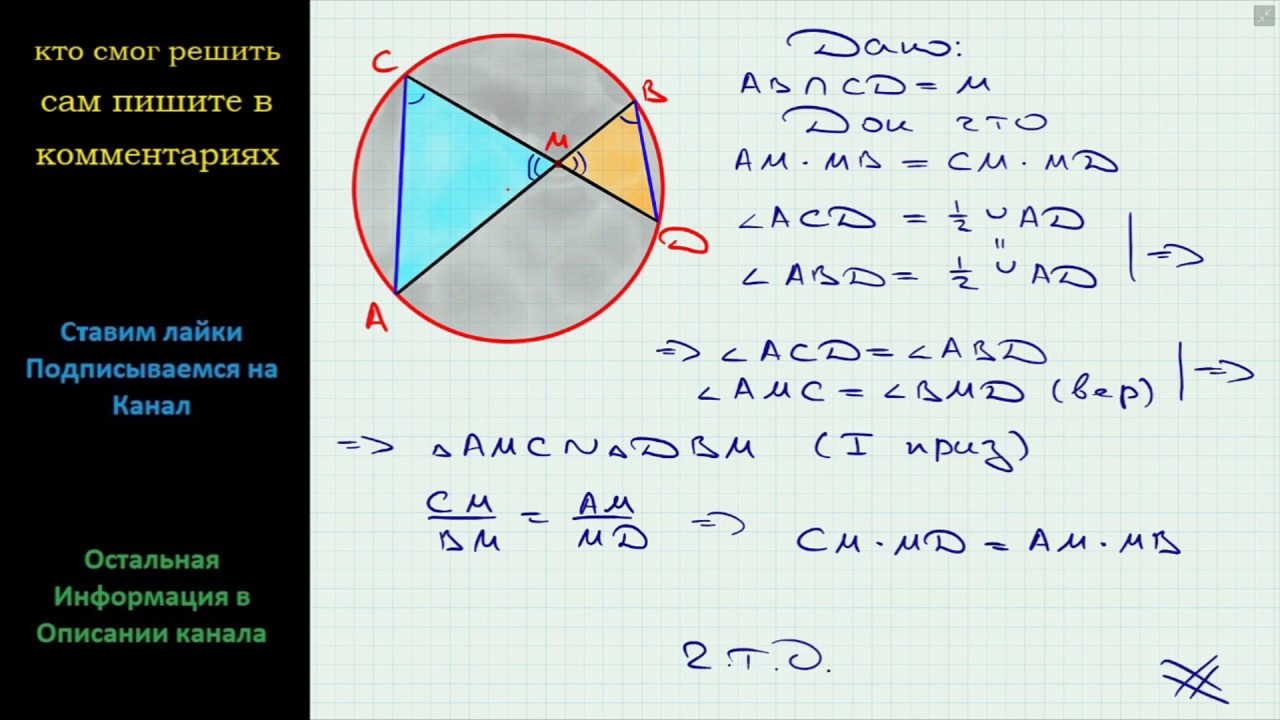
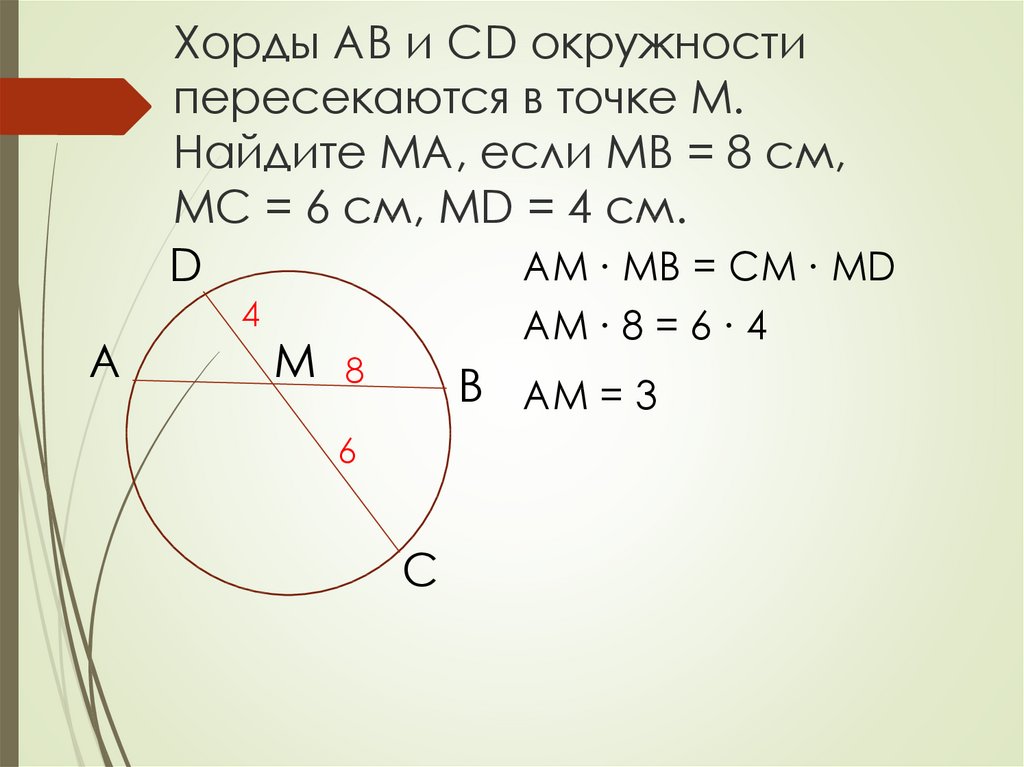
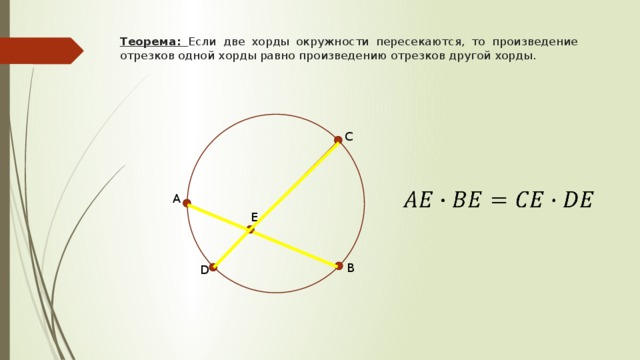
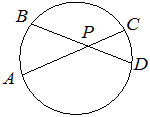Если хорды AB и CD окружности пересекаются в точке S, то AS • SB = CS • SD. 5. Если хорда AB проходит через внутреннюю точку M круга радиуса R и расстояние до M от центра OM = d, то AM • MB = R 2 - d 2.
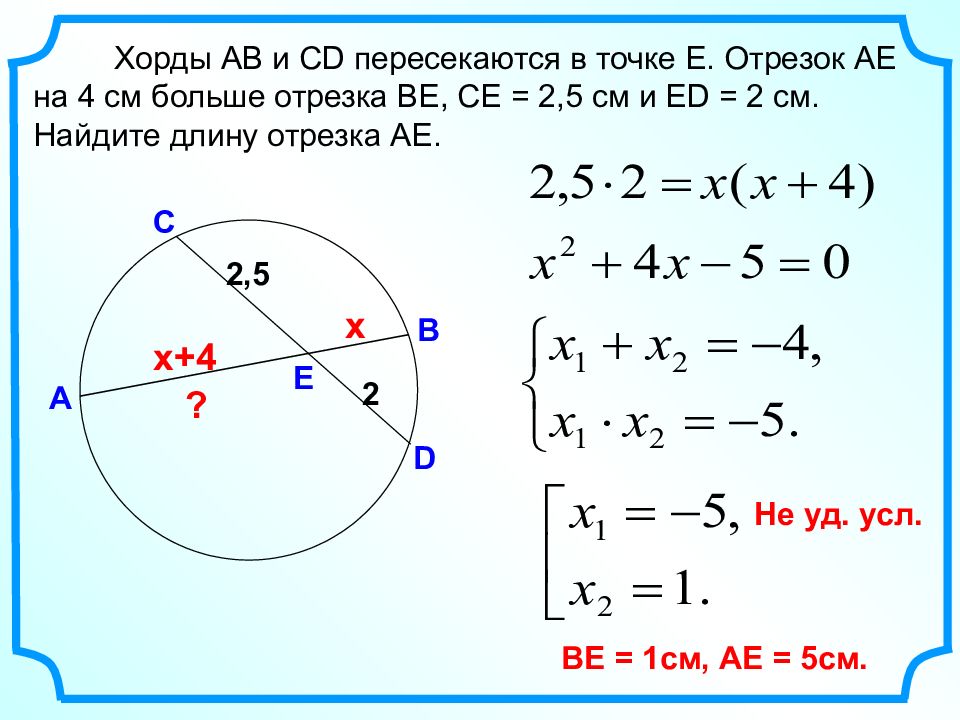
Если две хорды (АС и bd) окружности пересекаются (в точке Р), то произведение отрезков одной хорды (dp·bp) равно произведению отрезков второй хорды (ap·cp): dp·bp = ap·cp 20·9 = ap·15 180 = ap·15 ap = …
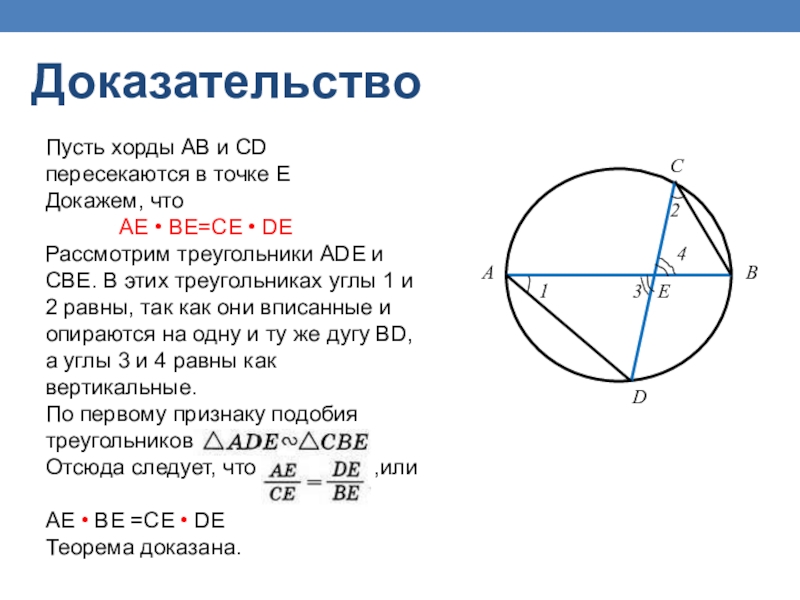
Теорема о пересекающихся хордах. Доказательство теоремы о пересекающихся хордах. Шаг 1. Рассмотрим окружность. Пусть две ее хорды АВ и CD пересекаются в точке Е. Докажем, что точка Е делит.
Отрезок, соединяющий любые две точки на окружности, называется хордой, а хорда, проходящая через центр, - диаметром (d). В С – хорда. С Е - диаметр. Свойства хорды и …
В окружности проведены хорды ab и cd , пересекающиеся в точке f. Найти длину отрезка ac, если af=6, df=8, bd=20. Дано: окружность (o; r), ab и cd — хорды, af=6, df=8, bd=20. Найти: …
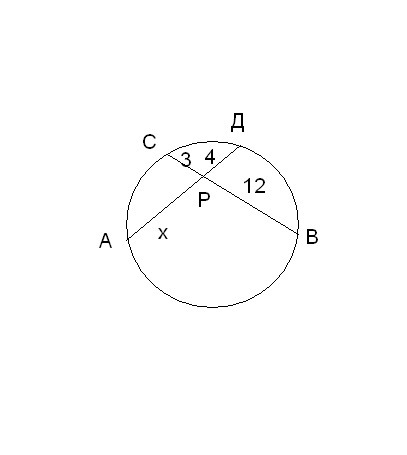
Решение: Если хорды АС и BD пересекаются в точке Р, то исходя из пропорциональности отрезков хорд, ВР* РD = АР*РС; АР = (ВР*РD)/РС АР = (12*25)/15=20. Ответ: АР=20. …
Если хорды АС и bd пересекаются в точке Р, то исходя из пропорциональности отрезков хорд, ВР* Рd = АР*РС; АР = (ВР*РD)/РС
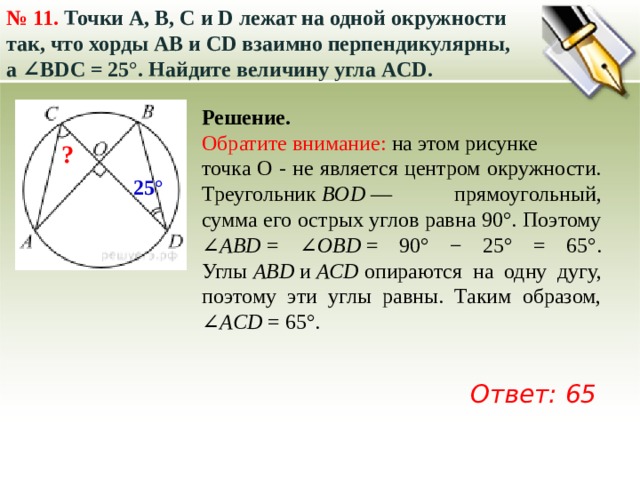
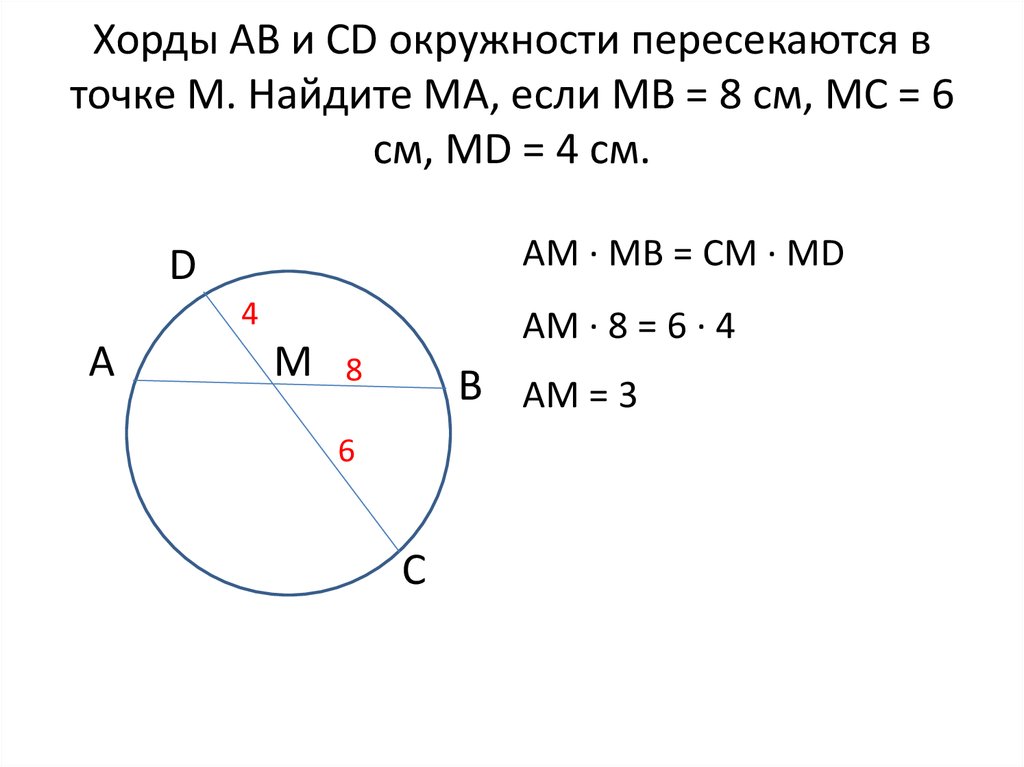В треугольнике РВД угол РВД равен вписанному углу СВД, который опирается на дугу СД, а следовательно, равен половине градусной меры дуги СД, а соответственно половине …
Еще по теме:
Еще по теме:
