Выписаны первые несколько членов геометрической прогрессии: -175; -140; -112;. Найдите пятый член этой прогрессии. Решение. Вспомним, что члены геометрической прогрессии …
Выписаны первые несколько членов геометрической прогрессии: 0,5; 2; 8;. Найдите сумму первых шести её членов.
Знаменатель геометрической прогрессии можно найти, разделив любой ее член на предыдущий: Каждый следующий член прогрессии получается из предыдущего …
Тысячи заданий с решениями для подготовки к ОГЭ−2024 по всем предметам. Система тестов для подготовки и самоподготовки к ОГЭ.
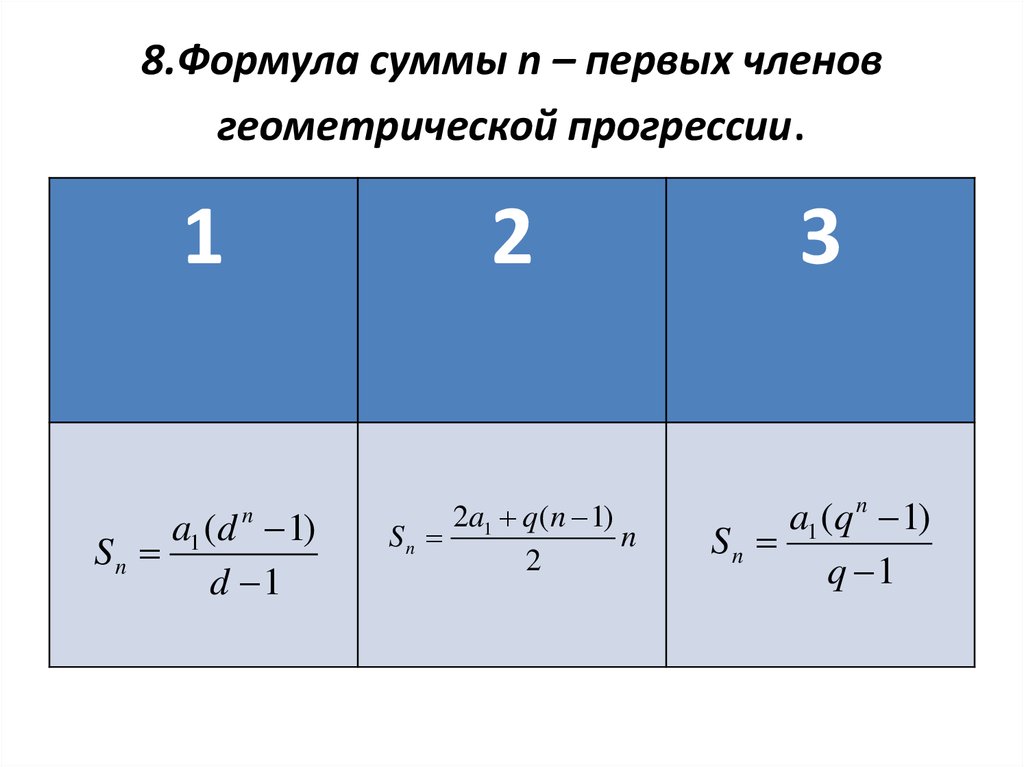
Сумма первых \ (n\) членов арифметической прогрессии \ (S_n=a_1+a_2+\dots +a_n\) может быть найдена по одной из двух формул: \ (S_n=\frac {a_1+a_n} {2}\cdot n\), если известно …
Выписаны первые несколько членов геометрической прогрессии: \ (-24; 108; -486;…\). Найдите ее четвертый член. \ ( (b_n)\) – геометрическая прогрессия, знаменатель …
Содержание. Что такое геометрическая прогрессия. Полезная информация. Формулы геометрической прогрессии. Свойство геометрической прогрессии. Бесконечно …
Какое из следующих чисел есть среди членов этой прогрессии? В поле для ответа запишите номер, соответствующий выбранному числу.
Выписаны первые несколько членов геометрической прогрессии: 3,5; 7; 14; … Найдите сумму первых 7 её членов. Решение: Ответ: 444.5
найдем знаменатель прогрессии: b2/b1=68/17=4. то есть, чтобы найти четвертый член прогрессии, нужно 272*4, получается 1088. Ответ: 4-ый член прогрессии = 1088.
Согласно условию задачи, дана геометрическая прогрессия bn, в которой первый член b1 = -1024, второй член b2 = -256, третий член b3 = -64.
Согласно условию задачи, даны первые три члена геометрической прогрессии bn: b1 = 125, b2 = -100, b3 = 80. Используя определение геометрической прогрессии, находим …
Выписаны первые три члена геометрической прогрессии: 7; –35; 175;. Найдите сумму первых четырёх её членов.
Выписаны первые несколько членов геометрической прогрессии: 7; -35; 175;. Найдите сумму первых четырёх её членов.
Найдем пятый член этой прогрессии, используя общую формулу при n=5, имеем: Ответ: -32,4. Все задания варианта
Для того, чтобы найти пятый член геометрической прогрессии, вычислим ее знаменатель по формуле: q = Bn+1 / Bn, где Вn+1 - каждый следующий член геометрической пргрессии.
Еще по теме:
Еще по теме:
