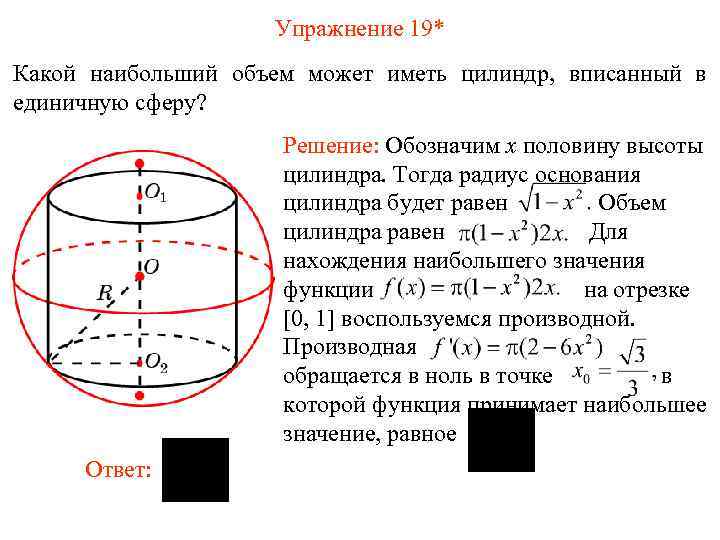
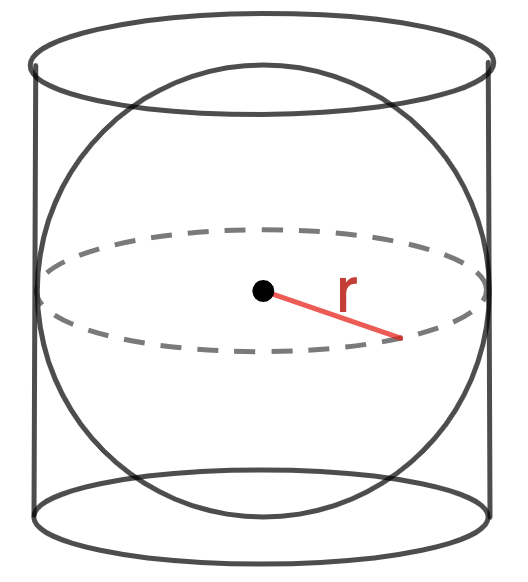
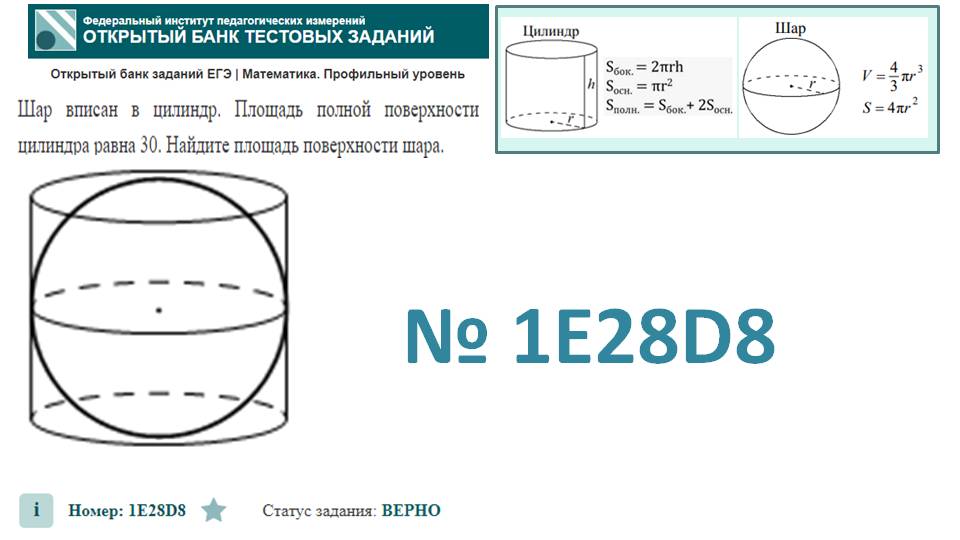
Найдите площадь полной поверхности цилиндра. Решение. Так как шар вписан в цилиндр, то радиус основания цилиндра равен радиусу шара R. А высота цилиндра равна …
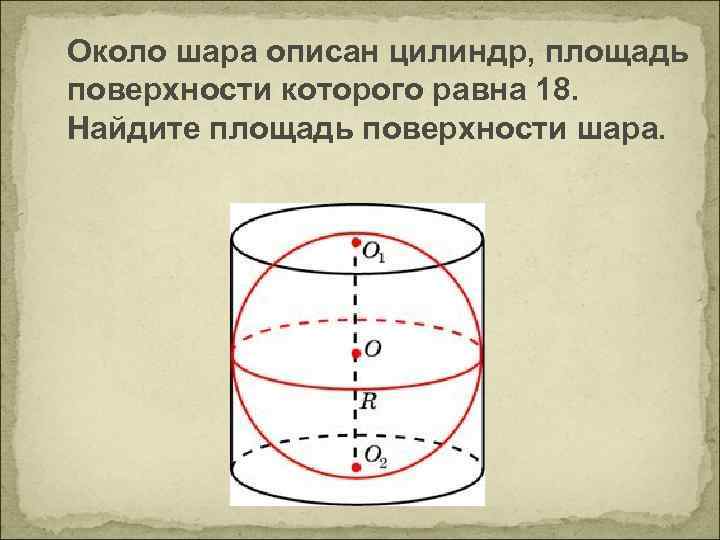
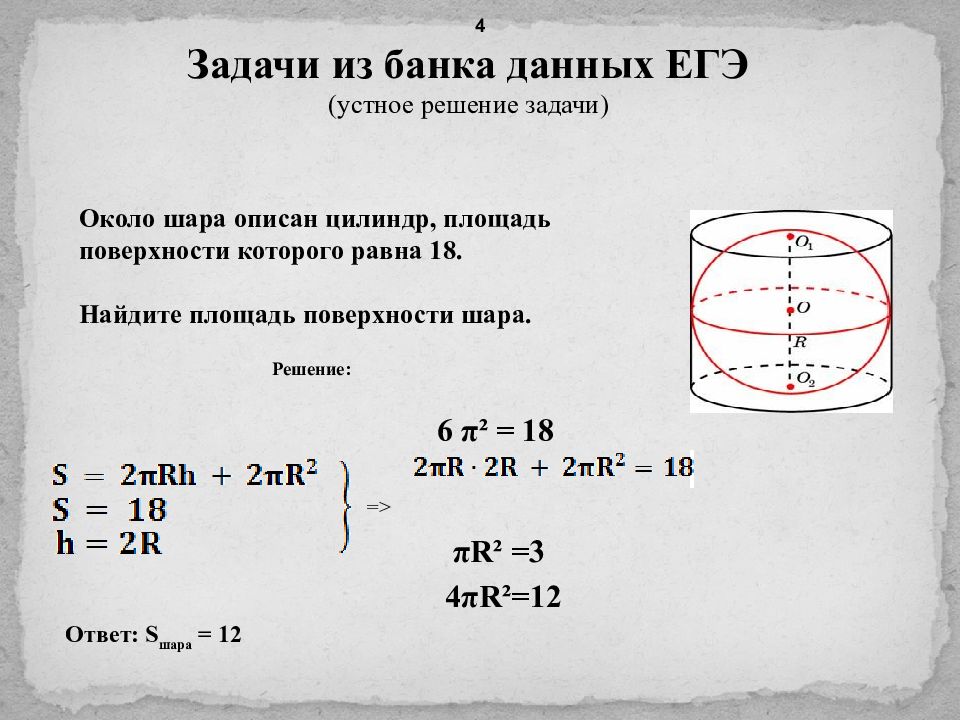
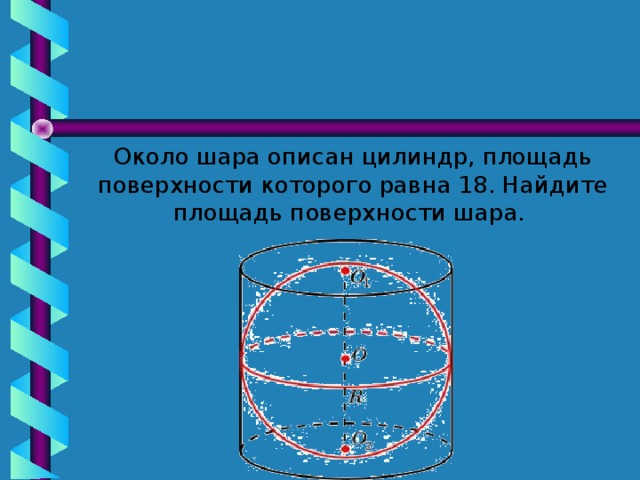
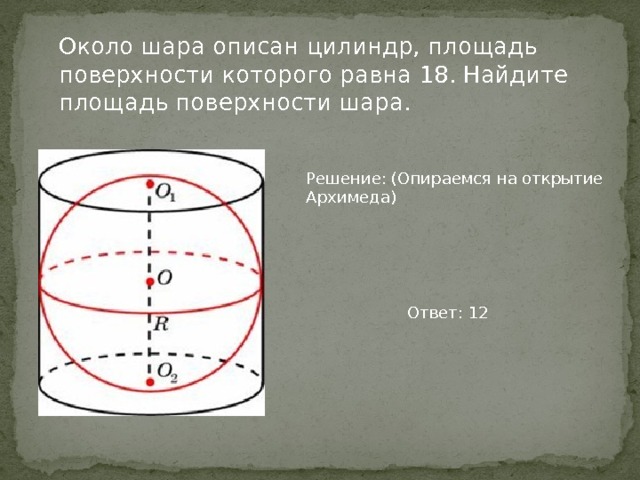
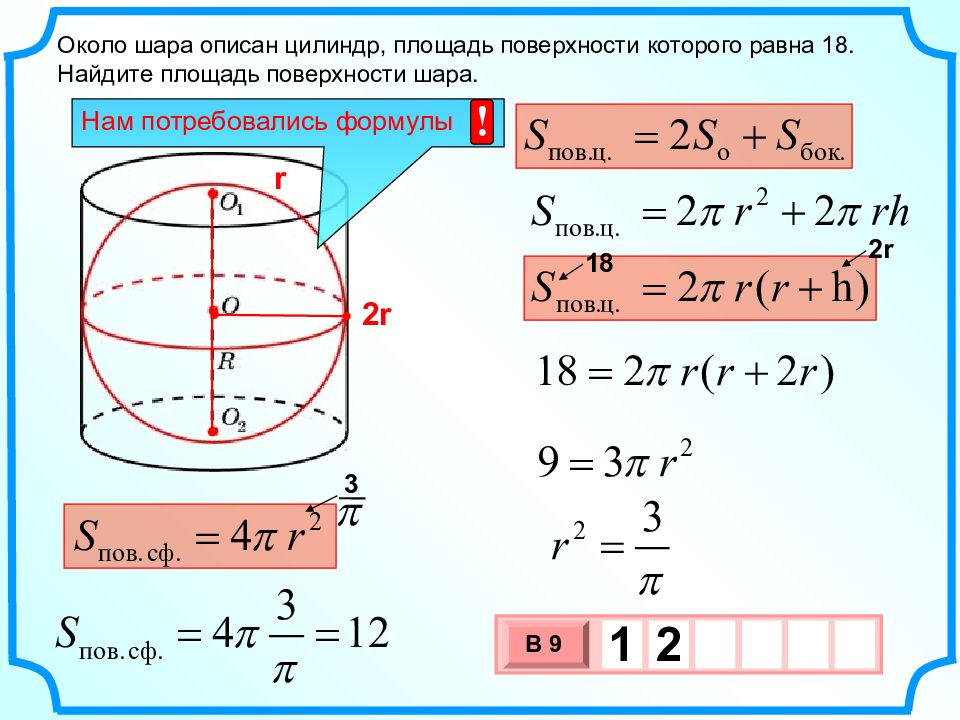
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 111. Найдите площадь поверхности шара.
Площадь поверхности шара равна 74. Найдите площадь полной поверхности цилиндра. Решение.
Площадь поверхности шара равна 74. Найдите площадь полной поверхности цилиндра Ответ: 111
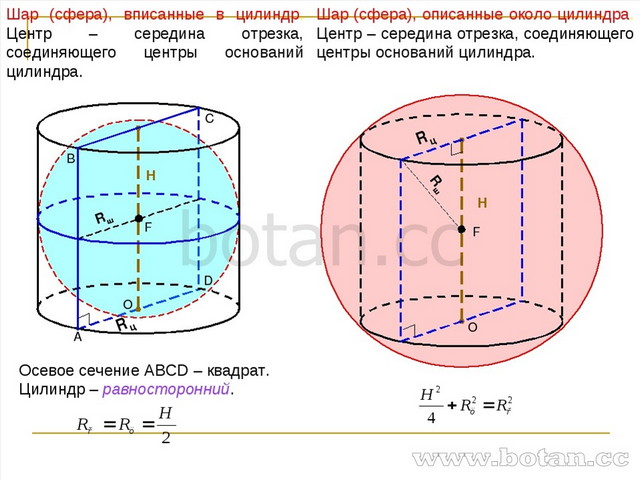
Если шар вписан в цилиндр, то цилиндр описан около шара. В цилиндр можно вписать шар тогда и только тогда, когда цилиндр …
Площадь поверхности шара вписанного в цилиндр с помощью онлайн калькулятора, зная площадь поверхности цилиндра.
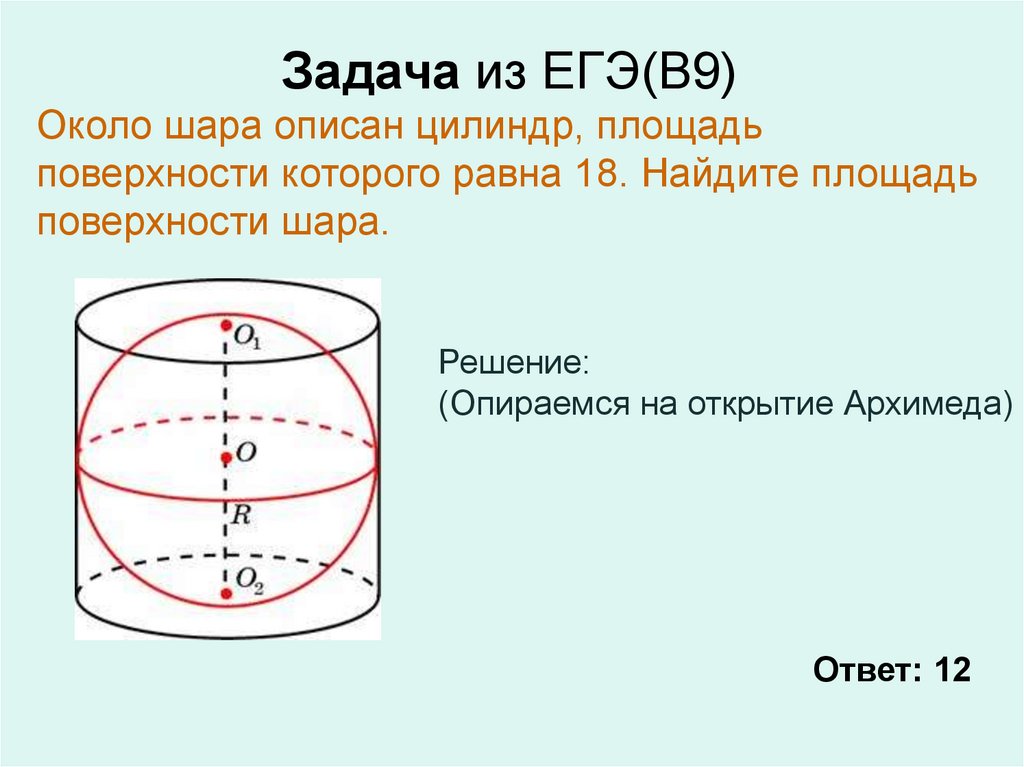Найдите площадь полной поверхности цилиндра. Задачи для подготовки к Задачи ЕГЭ профиль. Задания по теме Тела вращения. Условия, решения, ответы, тесты, курсы, …
Площадь поверхности шара вписанного в цилиндр, онлайн расчет позволит найти площадь поверхности шара, зная площадь описанного около него цилиндра, или площадь …
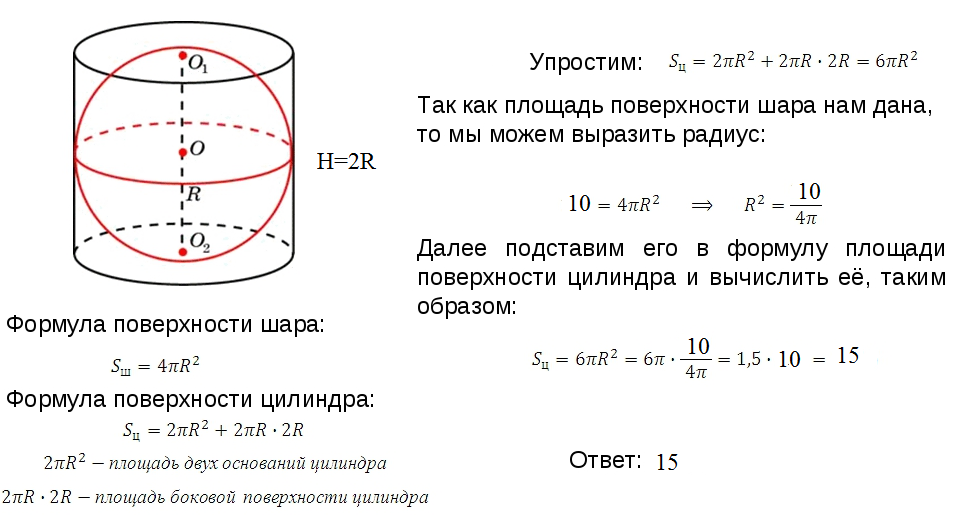
Площадь поверхности шара равна , отсюда имеем: . Площадь полной поверхности цилиндра находится по формуле , где h – высота цилиндра. В задании предполагается, …
если вписан -- радиусы шара и цилиндра совпадают (позначим r) и высота цилиндра равна диаметру, т. е. 2r. тогда поверхность цилиндра = 2*(пи*r^2) -- два основания + 2r*(2*пи*r) …
В данной публикации мы разберем варианты того, как можно вписать шар в цилиндр, а также, как исходя из этого определить его радиус (диаметр) и посчитать площадь …
Площадь полной поверхности цилиндра равна 57. Найдите площадь поверхности шара. Sц = 2πr * (h+r), где h – высота цилиндра, r – радиус основания …
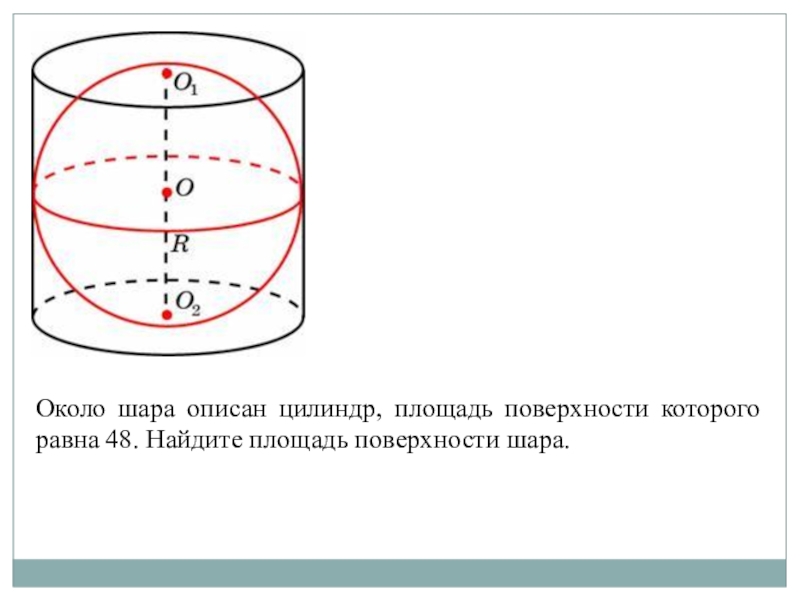
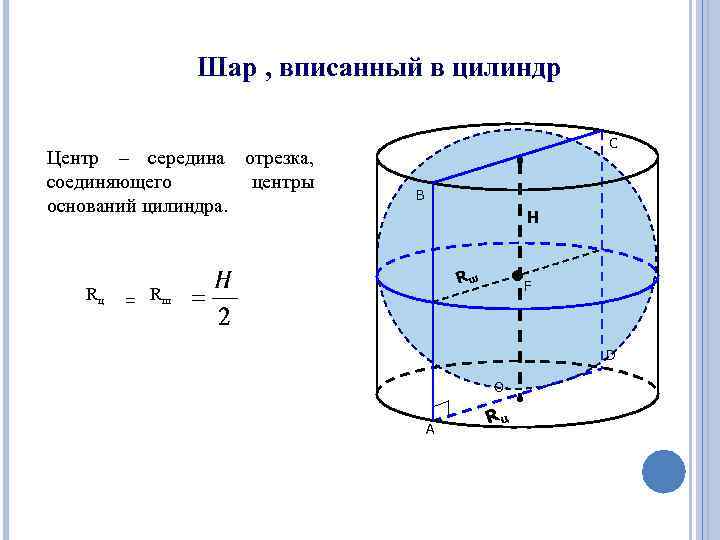
Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого …
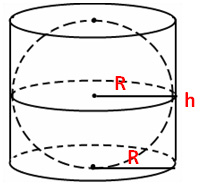
Пусть радиус шара равен R, тогда его диаметр равен 2 R, значит, высота цилиндра H равна 2 R. Находим площадь полной поверхности цилиндра: S полн. пов. цил. = 2 S осн. цил. + …
Для решения задачи воспользуемся формулами площади полной поверхности цилиндра и площади поверхности шара: Радиусы шара и цилиндра равны, .
Еще по теме:
Еще по теме:
