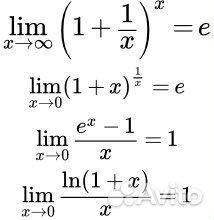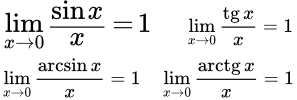Решение. Подставим $x=\infty$, получим неопределенность и для решения предела воспользуемся вторым замечательным пределом. $\lim _ {x \rightarrow \infty}\left …
Доказательство второго замечательного предела. При доказательстве мы будем использовать тот факт, что последовательность строго возрастает …
Примеры решений: 1 замечательный предел. Пример 1. Вычислить предел lim x → 0sin3x 8x. Решение. Первый шаг всегда одинаковый - подставляем предельное значение x = 0 …
Второй замечательный предел. В теории математического анализа доказано, что: Данный факт носит название второго замечательного предела. Справка: – это иррациональное …
Второй замечательный предел и его следствия. Предел последовательности обозначается буквой e: (1) Число e является иррациональным и приблизительно равно 2.718. Это …
Следствием второго замечательного предела являются следующие математические зависимости: $\underset{n\to \infty }{\mathop{\lim }}\,{{\left( 1+x …
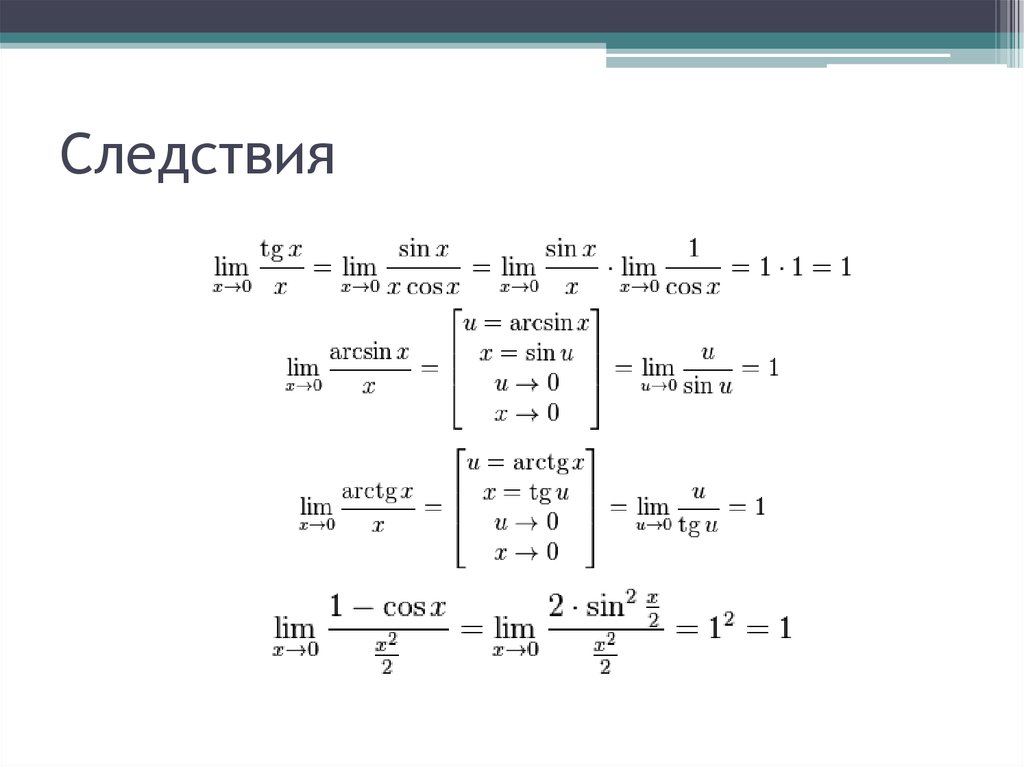
Следствия из второго замечательного предела. В данной теме мы разберём те формулы, которые можно получить, используя второй замечательный предел. Обычно формулы я …
Решение. Сразу отметим, что основание степени (т.е. 3x + 1 3x − 5) стремится к единице: lim x→∞ 3x + 1 3x − 5 = [∞ ∞] = lim x→∞ 3 + 1 x 3 − 5 x = 3+ 0 3− 0 = 1. При этом …
Подробные решения примеров с использованием второго замечательного предела и его следствий. Формулы, свойства и теоремы, применяемые при решении задач, допускающих решение с помощью.
Следствия второго замечательного предела. 1) 2) 3) 4) 5) 6) На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в …
Определение. Следствия из второго замечательного предела. Определение. Вторым замечательным пределом является предел, заданный выражением ниже: где e – это …
Пример 1. Используя второй замечательный предел, решите. lim x → ∞ (x + 4 x + 3) x + 3. \lim_ {x\to\infty} \bigg ( \frac {x+4} {x+3} \bigg)^ {x+3} limx→∞ (x+3x+4 )x+3. Решение. …
Пример для второго замечательного предела: \[ \lim_{x \to 0} (1 — 3x)^{\frac{1}{3x}} \] Решение: Воспользуемся заменой переменной. Пусть \( y = -3x \) , …
Подробный и понятный вывод второго замечательного предела для последовательностей через бином Ньютона.
Подставляем \(x_0=0\) в функцию, и получаем неопределенность: $$ \lim_{x\rightarrow 0}(cos2x)^\frac{1}{sin^2 3x}=\left[1^\infty\right] $$ Используем следствие из второго …
Еще по теме:
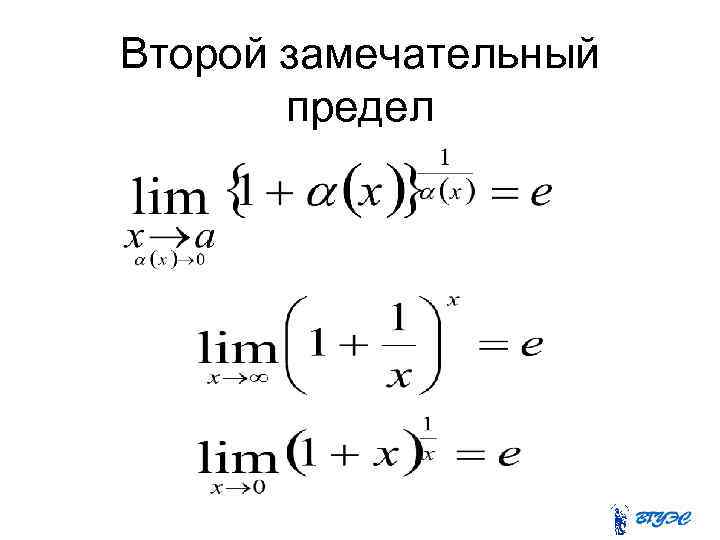
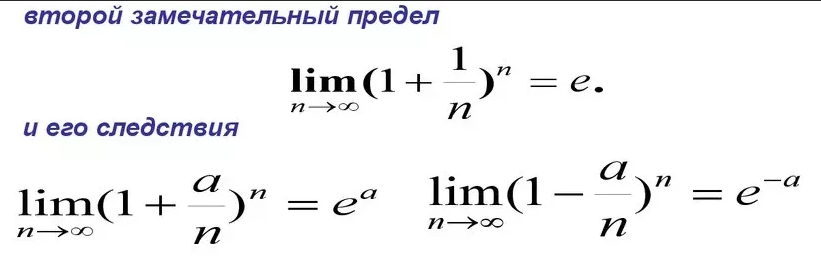
Еще по теме:
