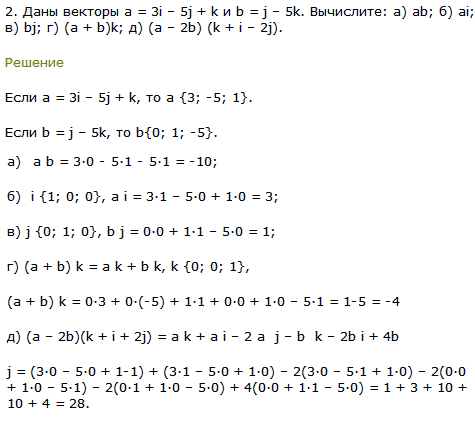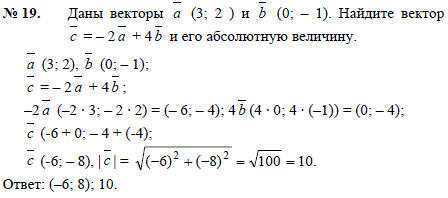Даны векторы \(\vec{a}(3;-1)\), \(\vec{b}(2;0)\) и \(\vec{c}(4;c_0)\). Найдите \(c_0\), если \((\vec{a}-\vec{b})\cdot\vec{c}=0\)
Даны векторы \vec{a}(-1; 3), \vec{b}(4; 1) и \vec{c}(2; c_0). Найдите c_0, если (\vec{a} + \vec{b}) \cdot \vec{c} = 0. Решение. Чтобы найти c_0, выполним следующие шаги: 1. Сложим …
Решение #1. Рассмотрим вариант решения задания из учебника Мерзляк, Полонская, Якир 9 класс, Вентана-Граф: 544. Даны векторы m (-2; 4) и n (3; -1). Найдите координаты …
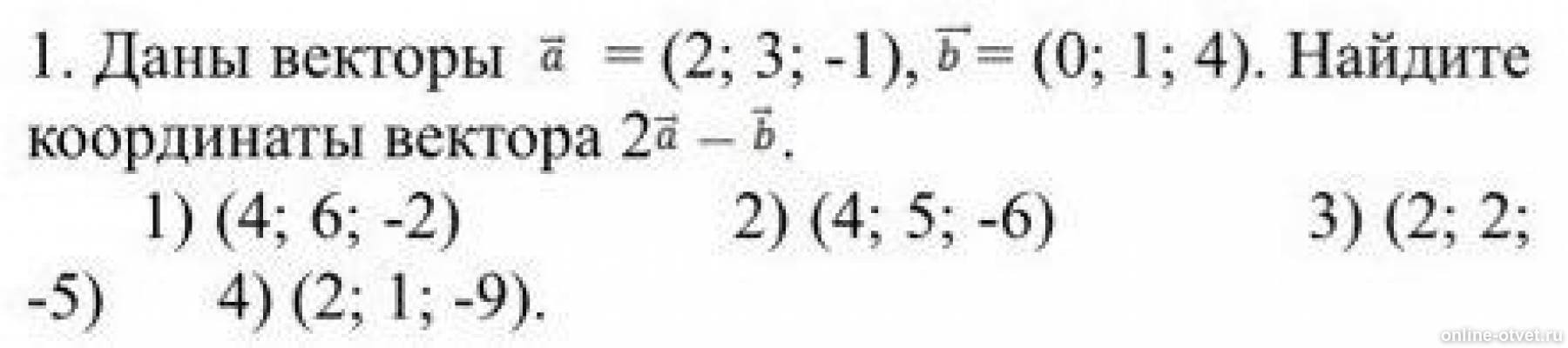Решение #2. Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 11 класс, Просвещение: 446 Даны векторы а {3; -1; 1}, b {-5; 1; 0} и с (-1; -2; 1}. Выясните, какой угол (острый, прямой или тупой) между …
Решение #2. Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 11 класс, Просвещение: 409 Даны векторы а {5; -1; 1}, b {-2; 1; 0}, с {0; 0,2; 0} и. d (--; 2-;--1. Найдите координаты векторов: а) a-b; б) b-a; 1 3.
Задача 12 # 68073. Даны неколлинеарные векторы и проведенные из одной точки, причем делит угол между векторами и пополам и равен Найдите отношение длины вектора к …
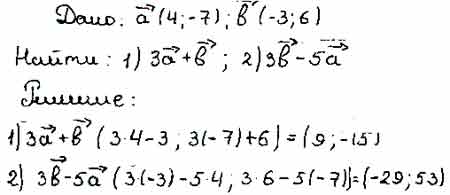Даны векторы: $\overrightarrow{a}\left(2;-4;0\right), \overrightarrow{b}\left(3;-1;-2\right)$ Выберите верные значения $m$ и $n$, при которых векторы $2\overrightarrow{a} …
Даны векторы a → (1; 2), b → (-3; 6), с → (4;-2). Найдите длину вектора a →-b → + c →.
Найти длину вектора $\overline{a}=(-4 ; 3)$ Решение. Используя формулу, получаем: $|\overline{a}|=\sqrt{(-4)^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5$
Векторным произведением вектора на вектор называется вектор, обозначаемый символом и определяемый следующими тремя условиями: 1). Модуль вектора равен , где - угол …
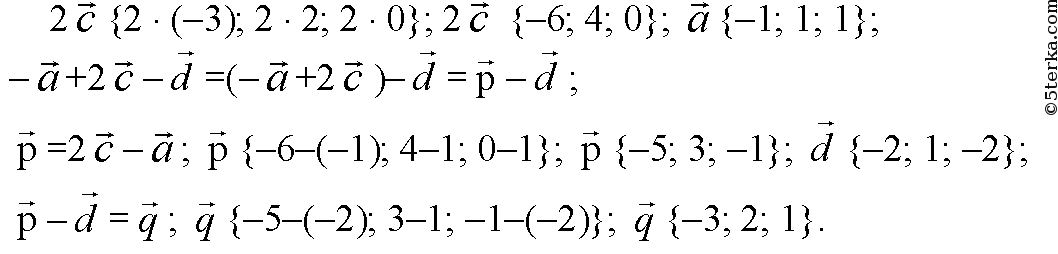Даны векторы \(\vec{a}(1;3)\) и \(\vec{b}(-4;2)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
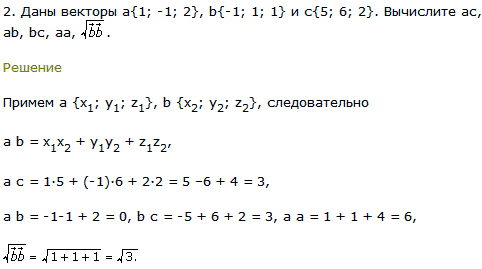Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач. …
Подробное решение задания ЕГЭ по математике (профиль). Даны векторы a(2; -5), b(6; 3) и c(4; 7). Найдите длину вектора a - b - c.
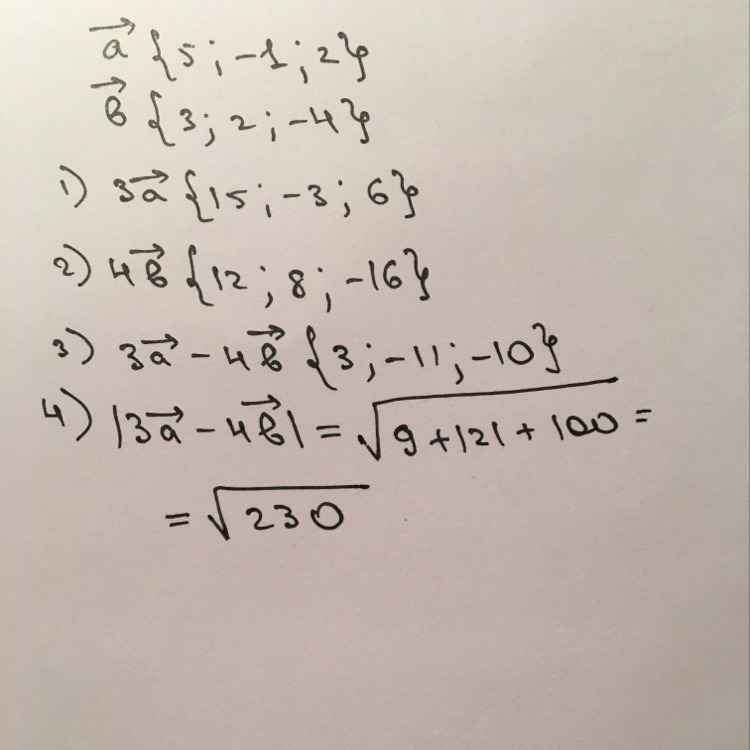Решение #2. Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 11 класс, Просвещение: 407 Даны векторы а {3; -5; 2}, 5 {0; 7; -1}, cj^;0;0 |и d {-2,7; 3,1; 0,5}. …
Найти угол между векторами a = {3; 4} и b = {4; 3}. Решение: Найдем скалярное произведение векторов: a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Еще по теме:
Еще по теме:
