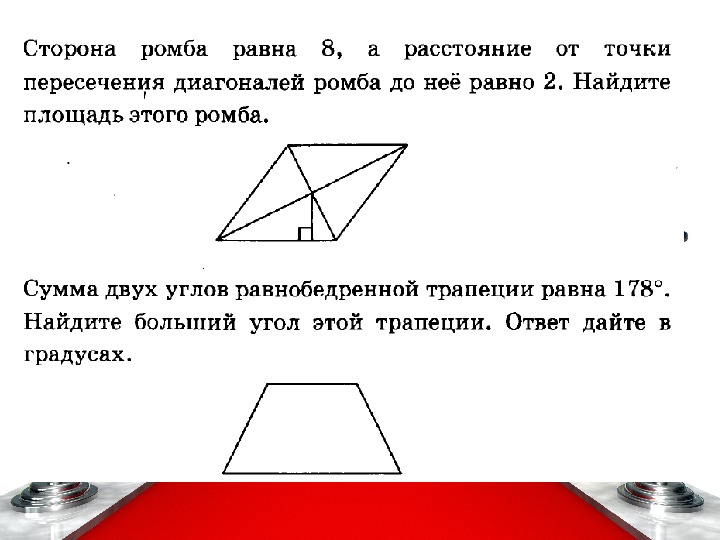
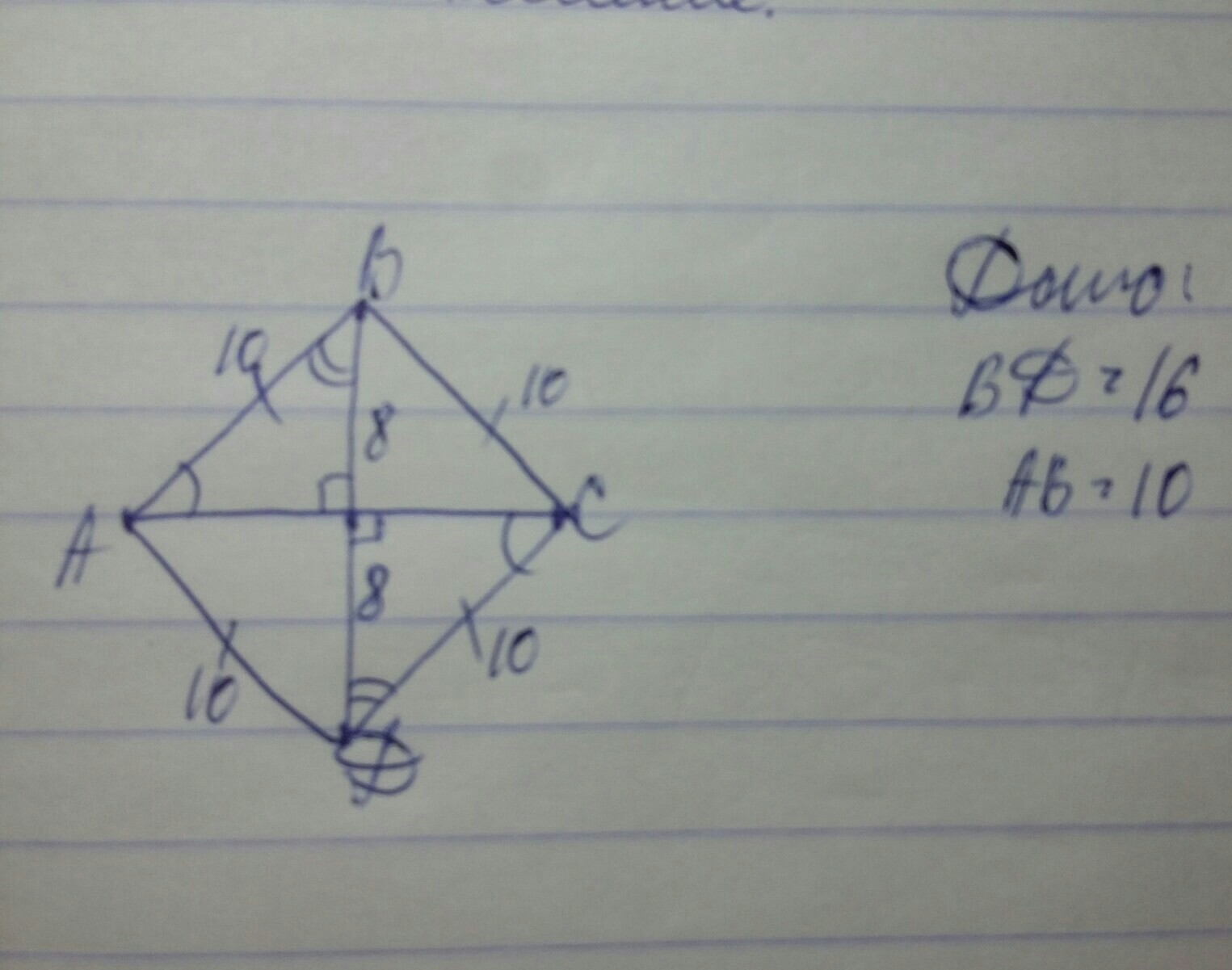
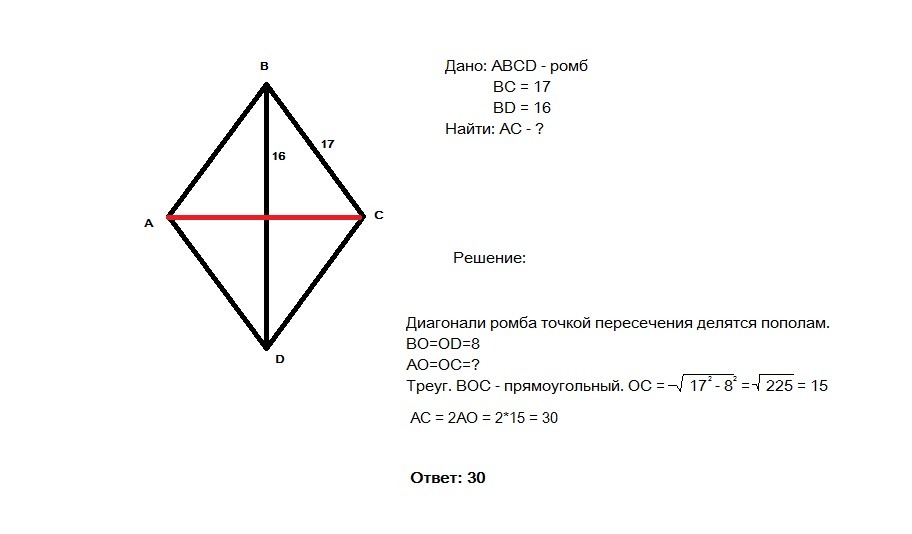
Решение: Пусть abcd — ромб, ad = 10; om = 3. 2 Продлим om до противоположной стороны ad. Получим, что MN — высота ромба (диаметр вписанной окружности), тогда MN = 2 * …
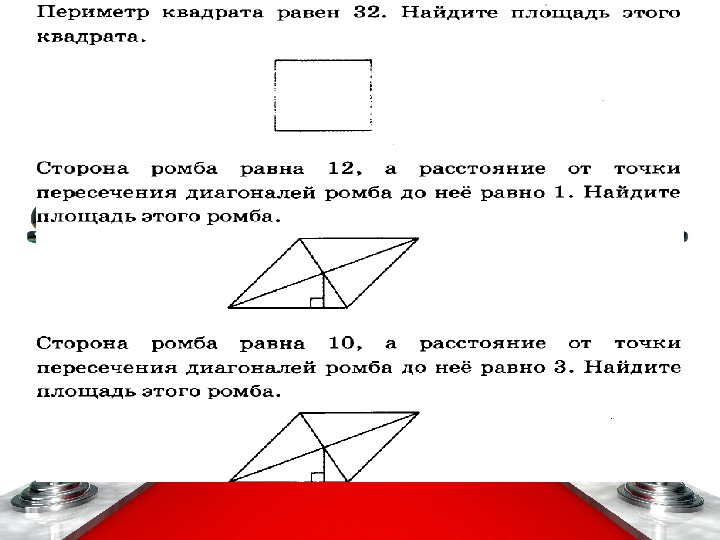
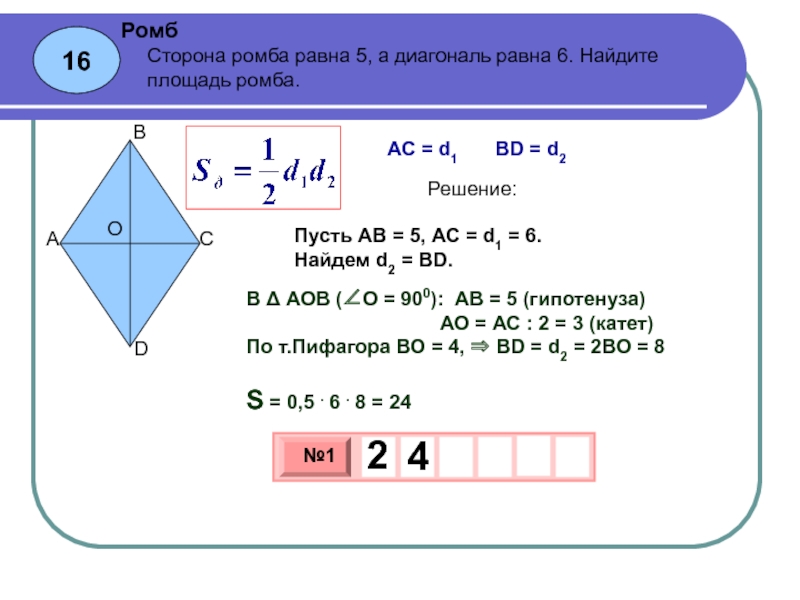
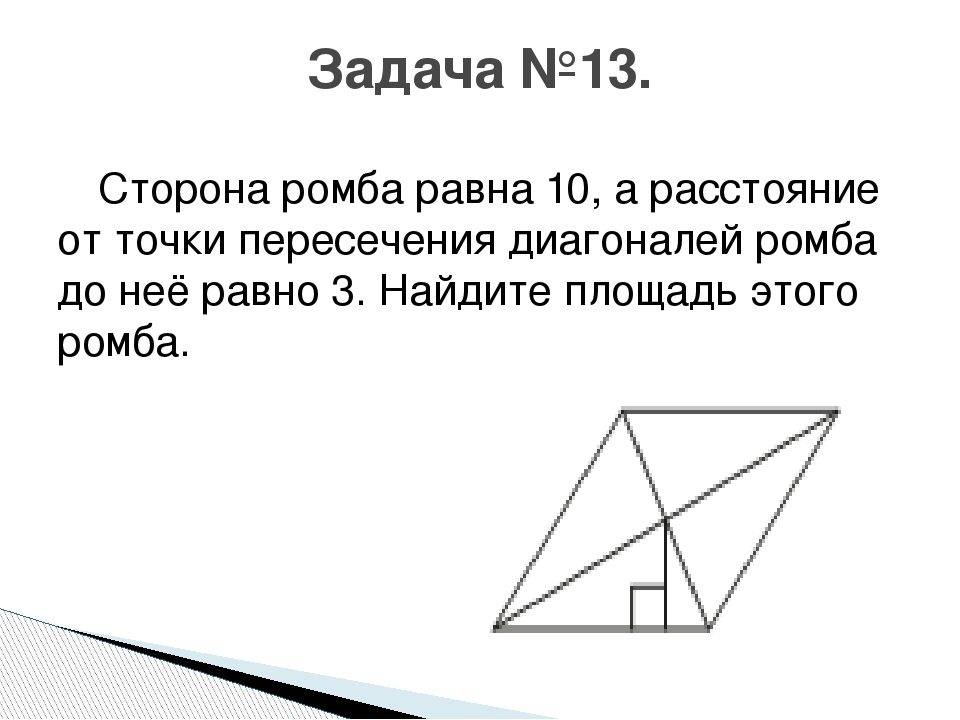
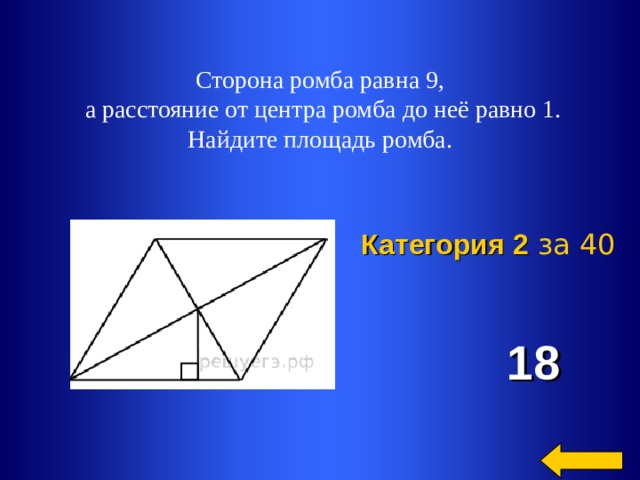
Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба. Решение: S = аh = 10 * 2 * 3 = 60 Ответ: 60. 857D14
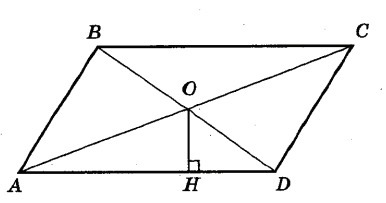В данном случае сторона ромба равна 10. Подставляем значение: Площадь ромба = 10^2 = 100 квадратных единиц.
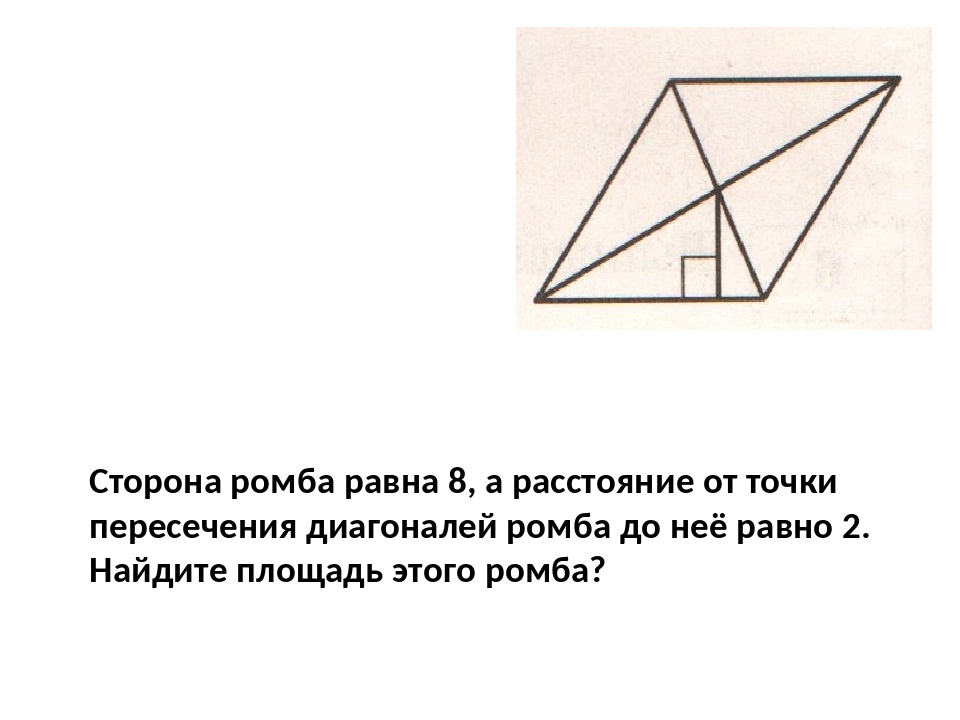
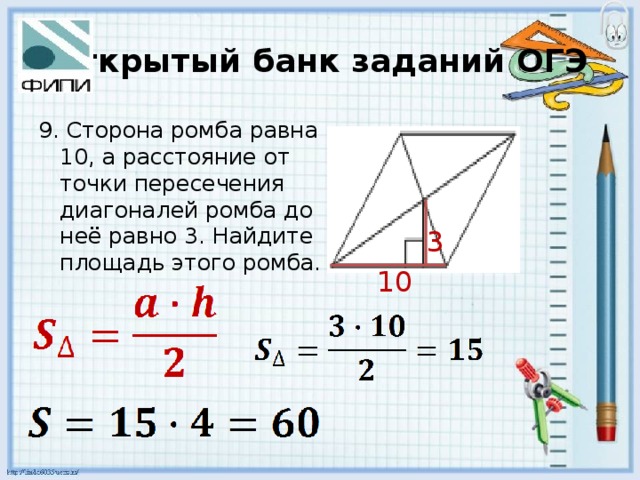Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба
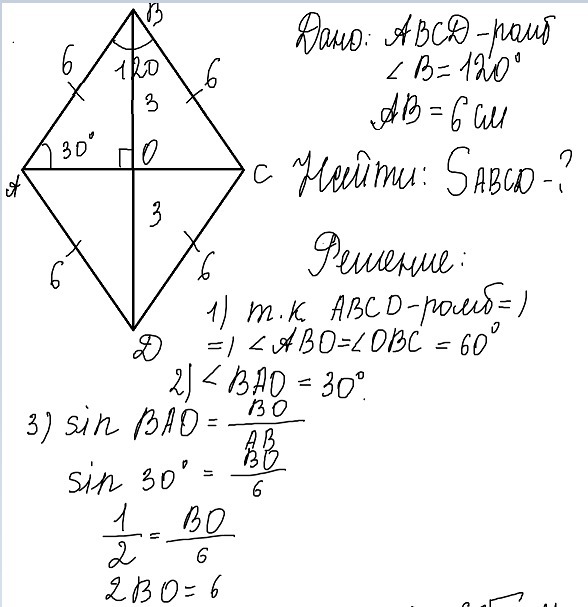
Задание 3. Сторона ромба равна 10, острый угол равен 30°. Найдите радиус окружности, вписанной в ромб. Решение. Можно заметить, что диаметр окружности совпадает с …
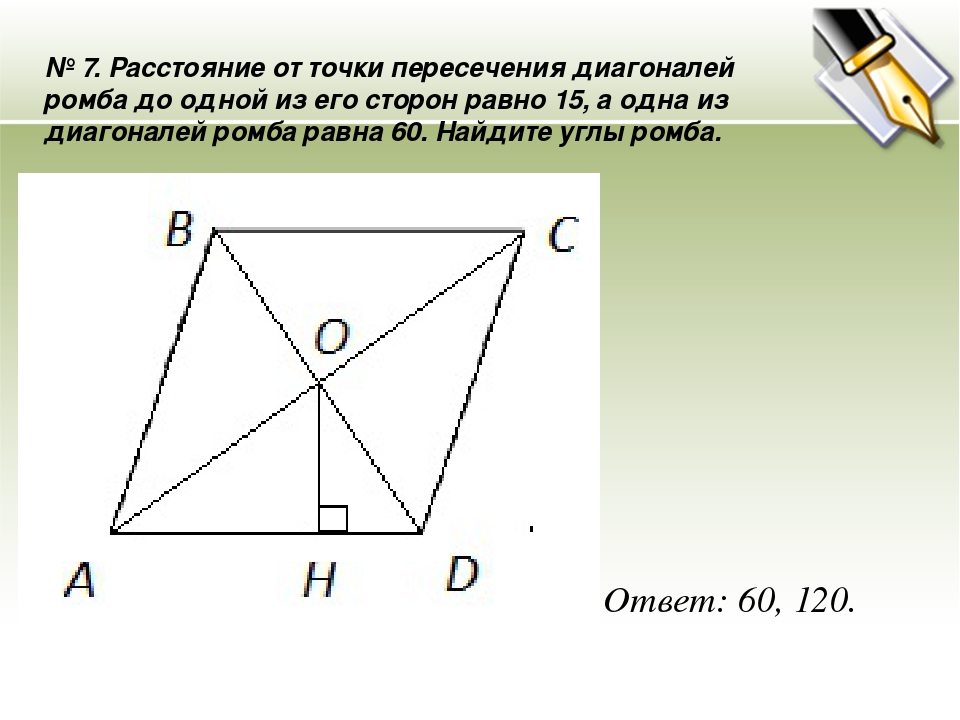
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76.
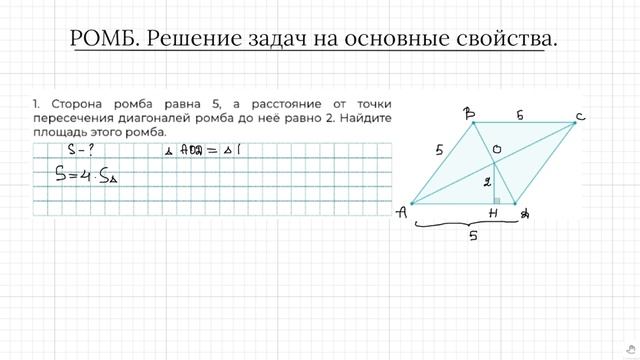
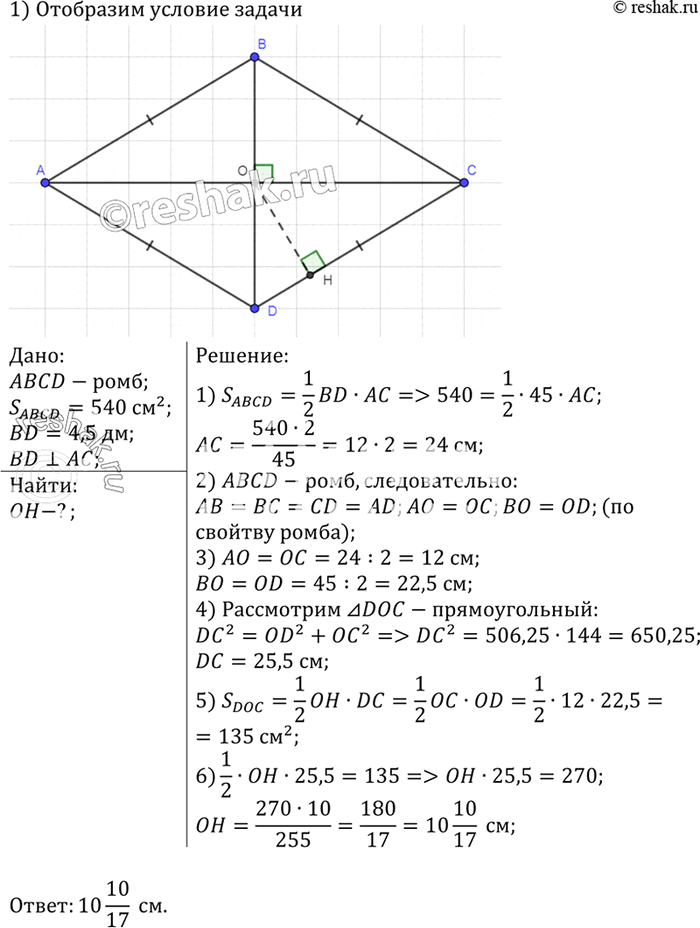
Обозначим точку пересечения диагоналей ромба АВСД за О, а основание высоты из точки О на сторону АД за Е ( учётом того, что расстояние от точки пересечения диагоналей …
Пусть abcd - ромб, ad = 10; om = 3. Продлим ОМ до противоположной стороны ad. Получим что mn - высота ромба (диаметр вписанной окружности), тогда mn = 2*mo = 2*3 = 6. …
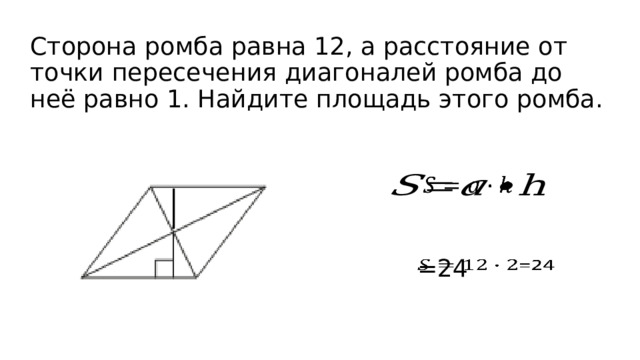Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё равно 3. Найдите площадь этого ромба.
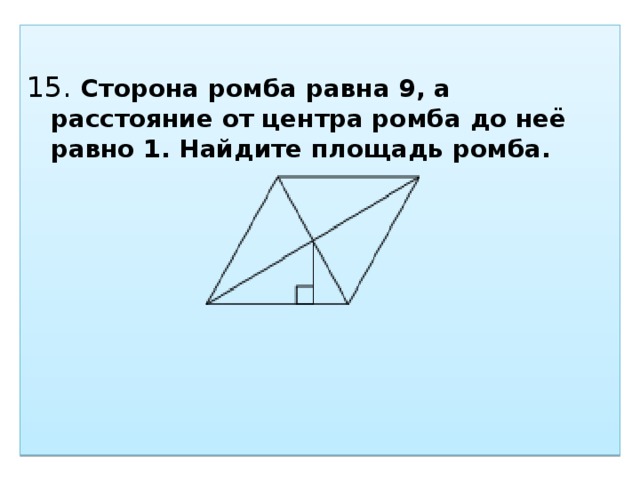
Сторона ромба равна 10, а расстояние от центра ромба до нее равно 3. Найдите площадь ромба. Ответ: 60
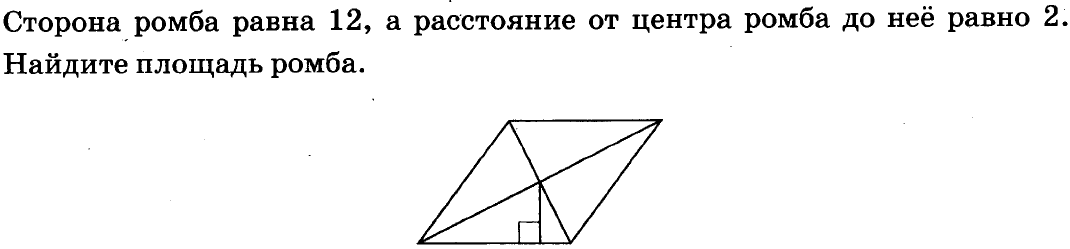Сторона ромба равна 10, а растояние от точки пересечения диагоналей до стороны = 3 найти площадь ромба +5
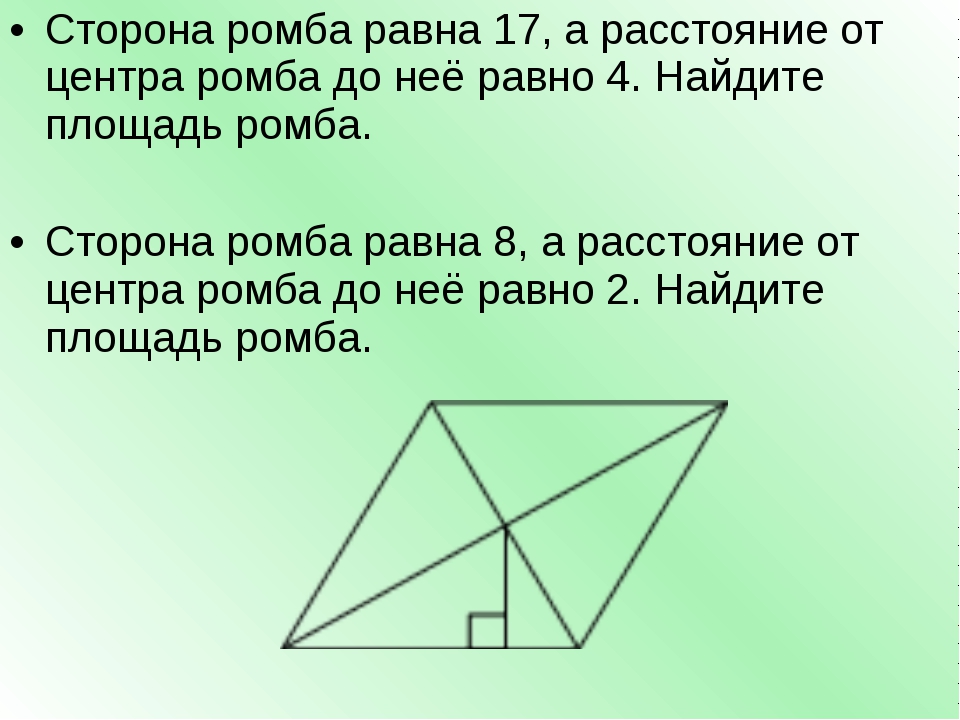Пусть abcd - ромб, ad = 10; om = 3. Продлим ОМ до противоположной стороны ad. Получим что mn - высота ромба (диаметр вписанной окружности), тогда mn = 2*mo = 2*3 = 6. …
сторона ромба равна 10 а один из его углов равен 30 найдите расстояние от точки пересечения диагоналей до стороны ромба. Лучший ответ. Любавушка, 8 лет назад. …
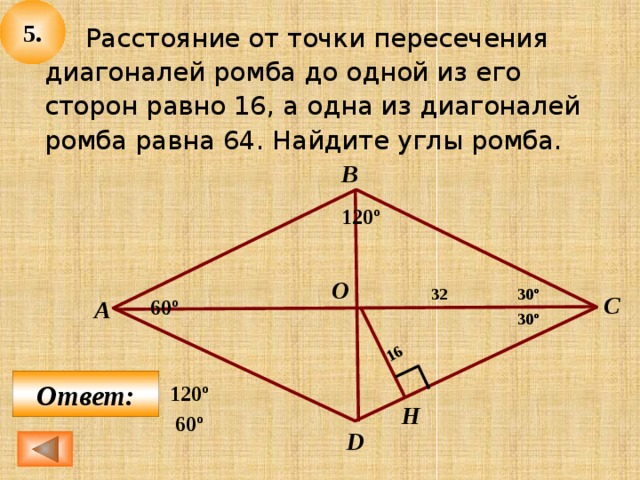Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 13, а одна из диагоналей ромба равна 52.
Сторона ромба равна 10, а расстояние от точки пересечения диагоналей ромба до неё 3. Найдите площадь этого ромба. Посмотрите правильный ответ!
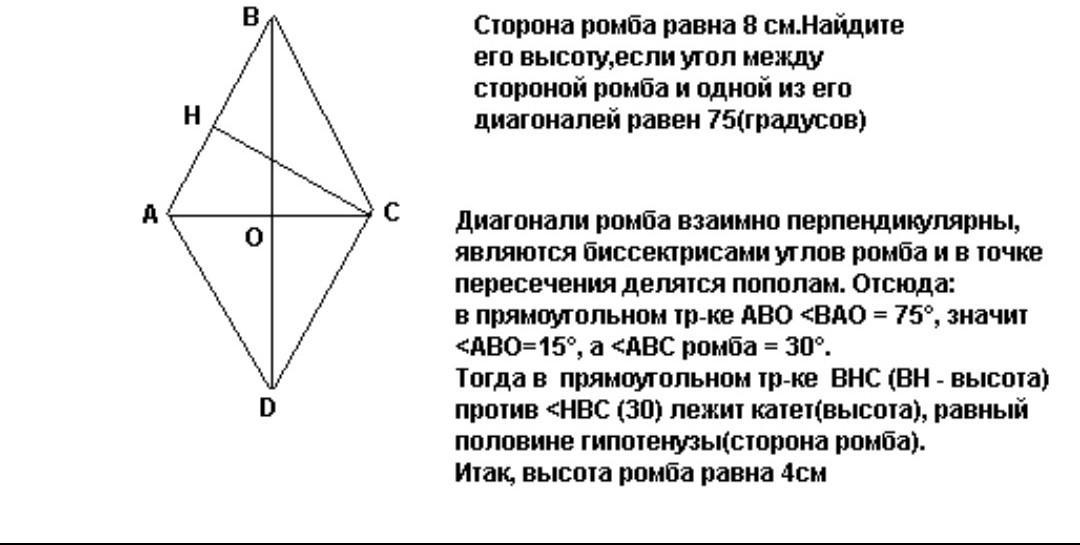
ОМ - высота треугольника АВО, проведённая к гипотенузе АВ. ОМ одновременно расстояние от центра ромба до его стороны. В прямоугольном тр-ке h=ab/c. …
Еще по теме:
Еще по теме:
