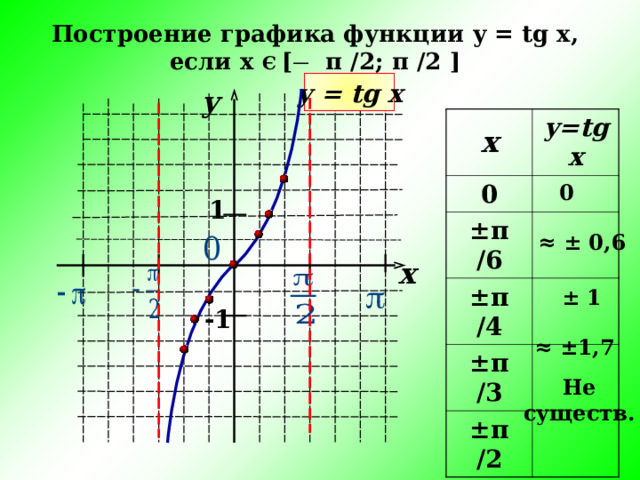
Рассмотрим свойства тангенса. Область определения функции тангенс — это множество R всех действительных чисел, кроме π/2 + π·n, где n ∈ Z (D (tg x)=R\ { π/2 + π·n }). Т.е. это означает, что функция tg x определена для x∈ (-∞; π/2 + π·n) ∪ ( π/2 + π·n; +∞).
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) …
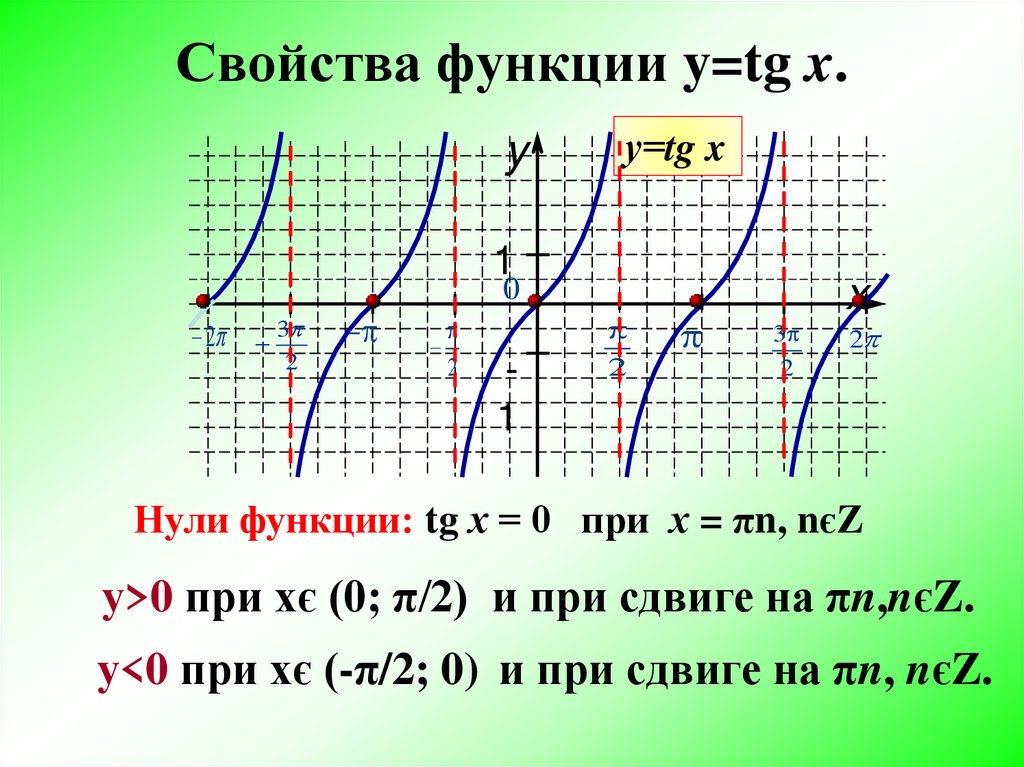
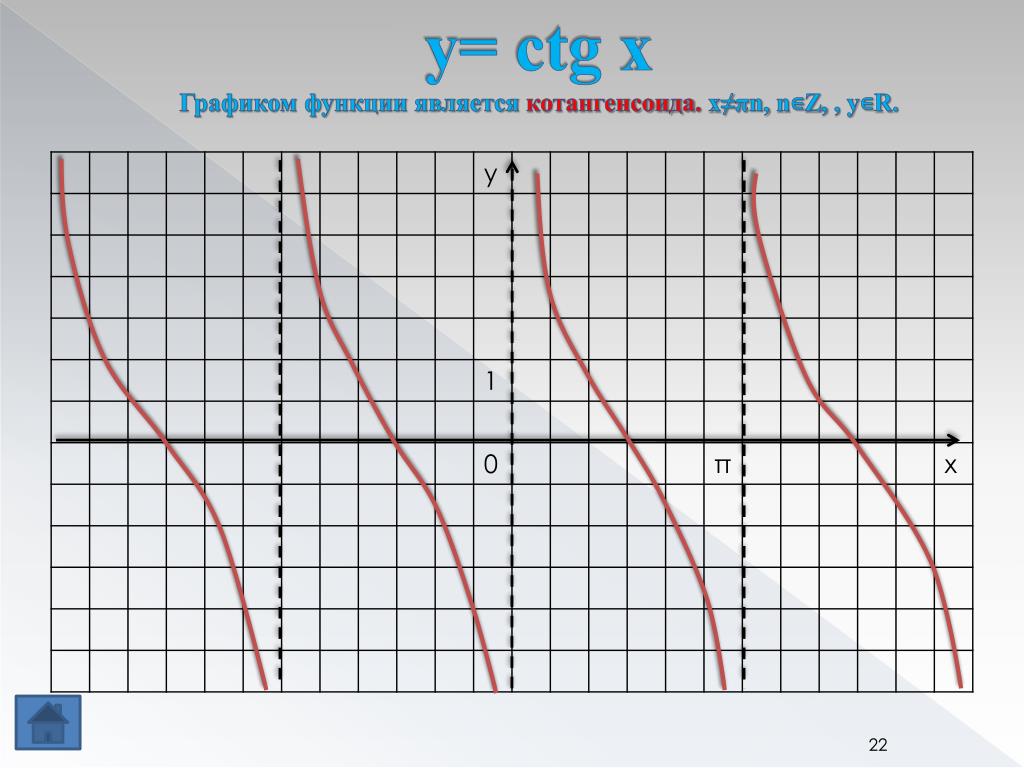
Свойства функции и график. Промежутки знакопостоянства тангенсоиды. Координаты точек пересечения тангенсоиды. Определим по графику тангенса.
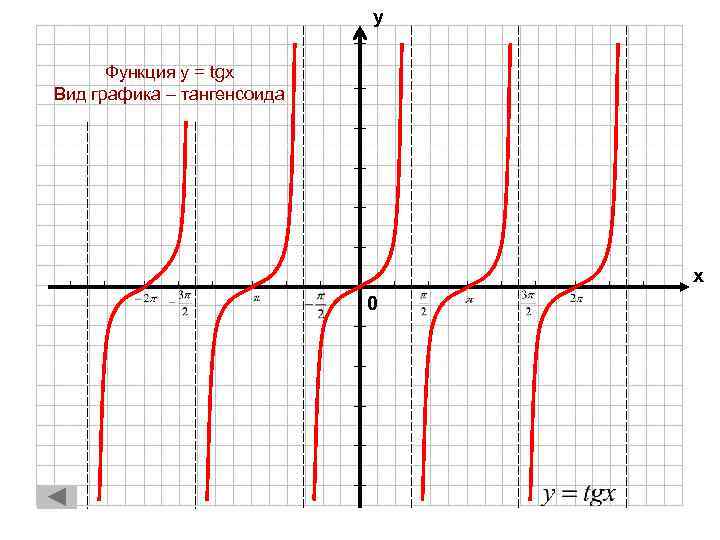
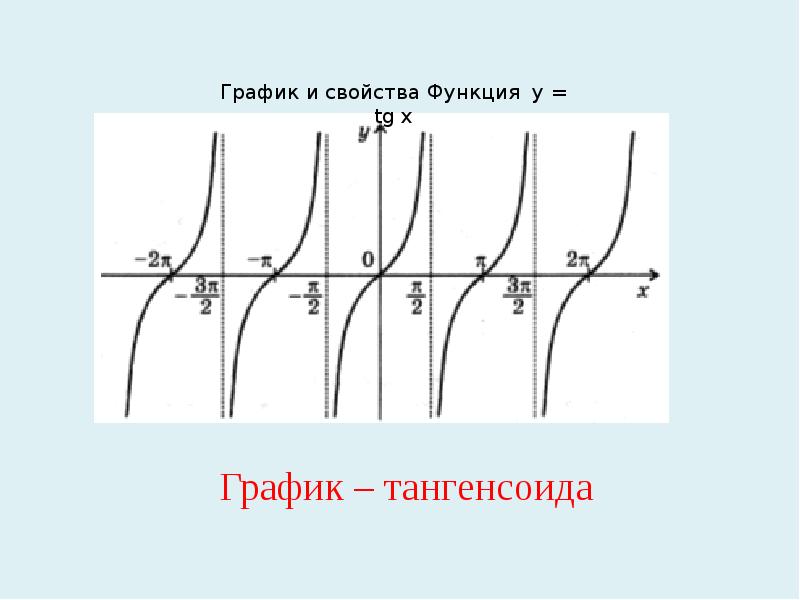
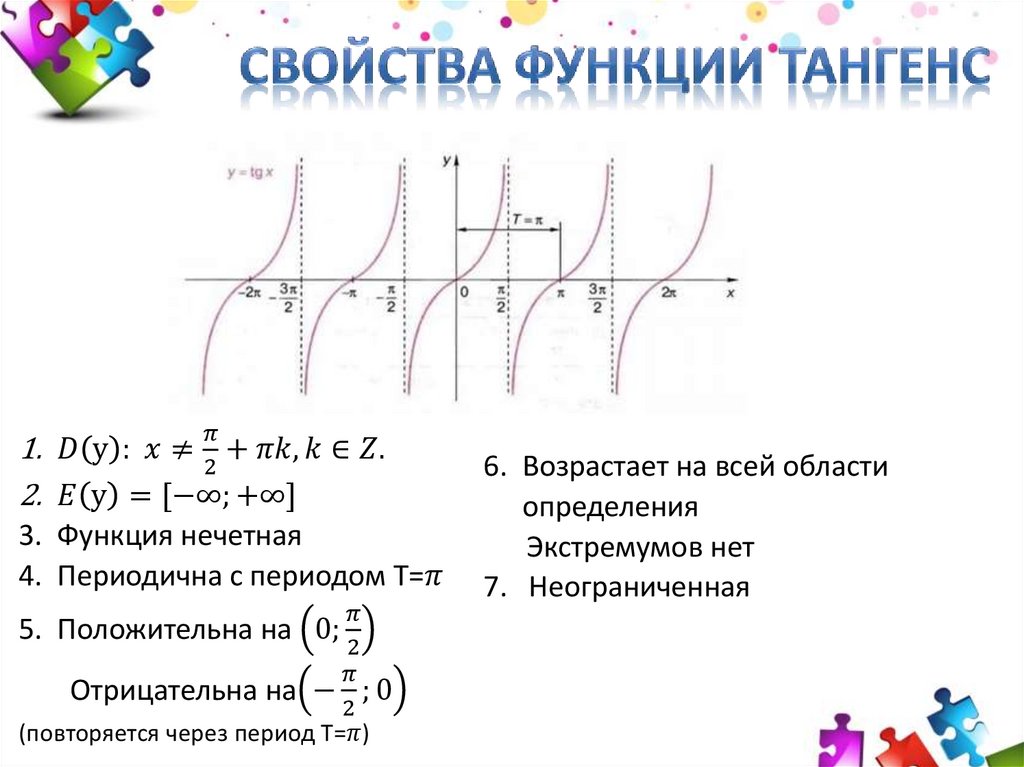Тангенсоида –график функции у = tgx; плоская кривая, изображающая изменение тангенса в зависимости от изменения его аргумента (угла).
Перед изучением функции тангенса и её свойств, вспомним понятие самого тангенса. Определение тангенса можно ввести двумя способами: с помощью прямоугольного треугольника и с помощью …
Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения …
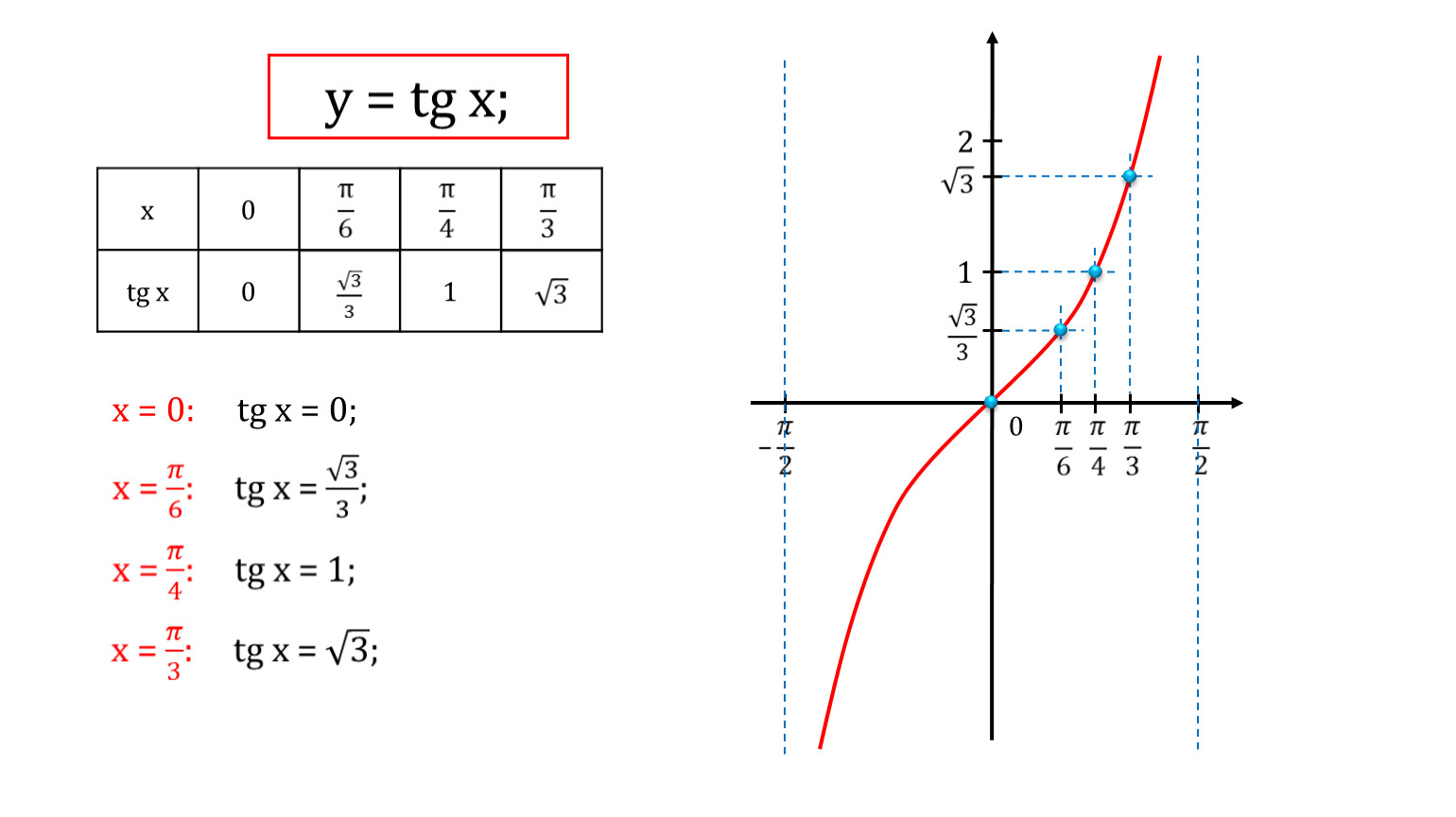
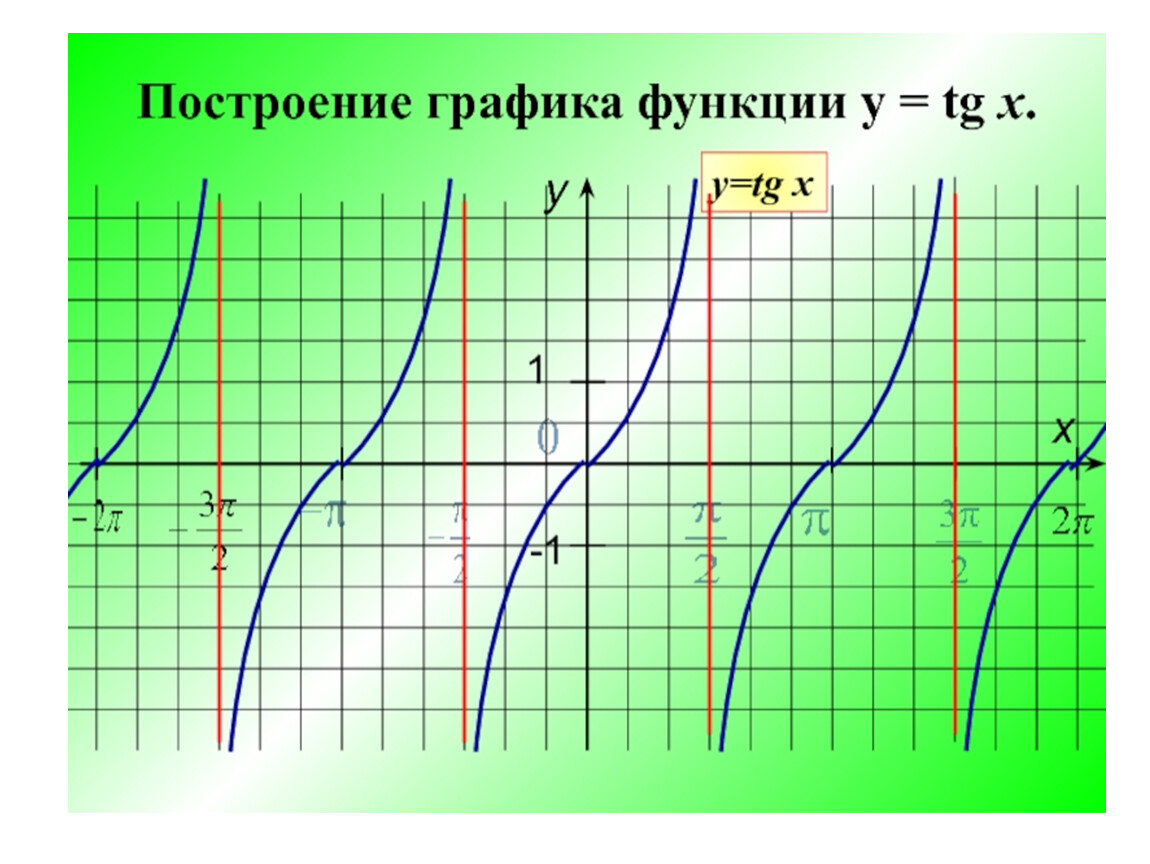
Как построить график танегнса. Свойства функции тангенс. Вывод свойств функции тангенс.
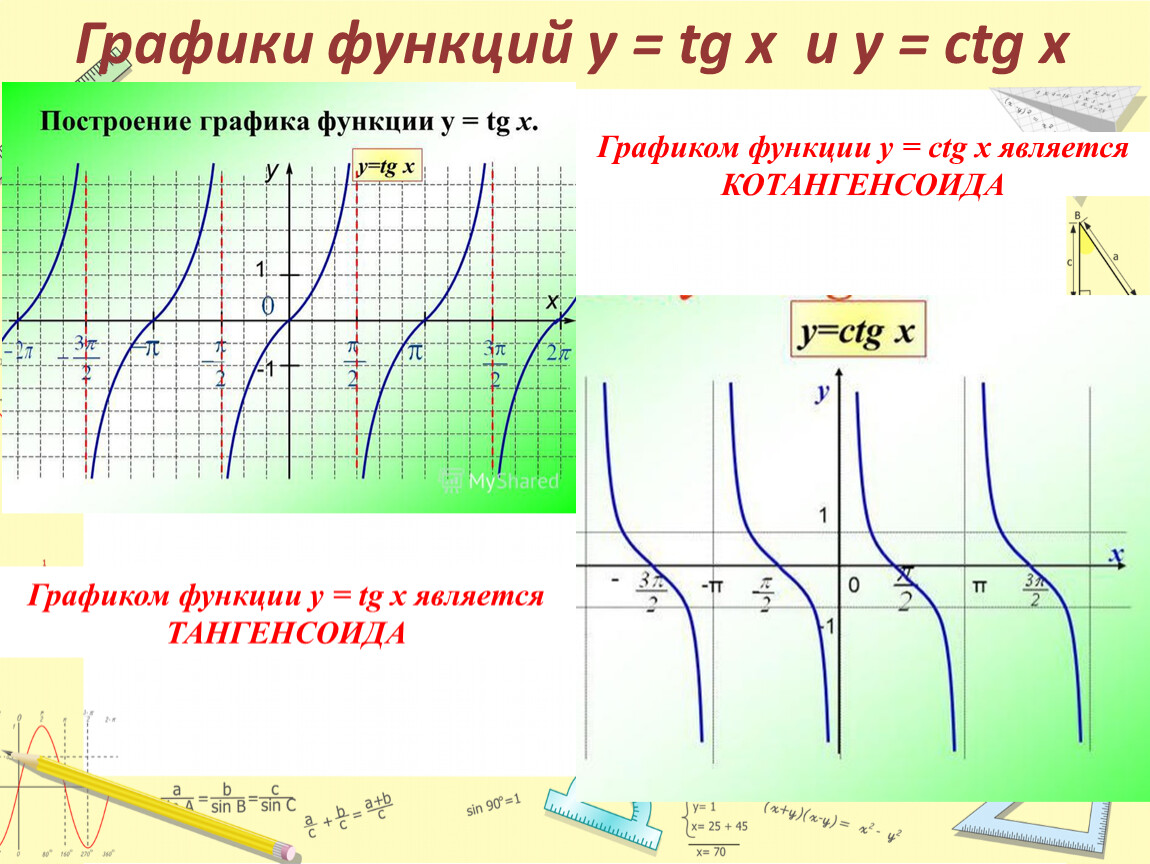
Мы рассмотрим свойства функции у = tg x ( игрек равно тангенс икс), у = ctg x( игрек равно котангенс икс), построим их графики.
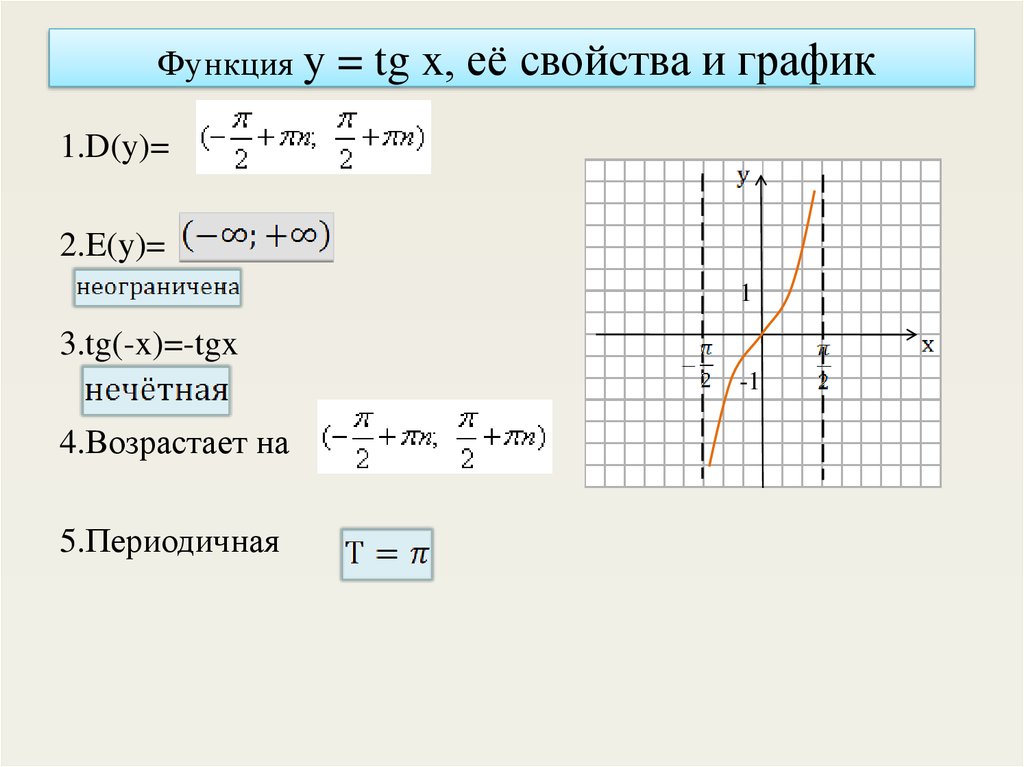
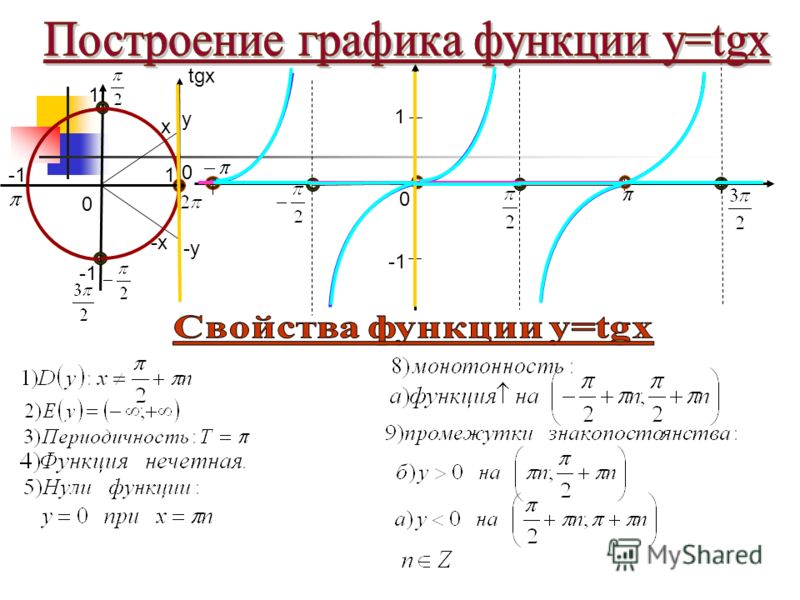
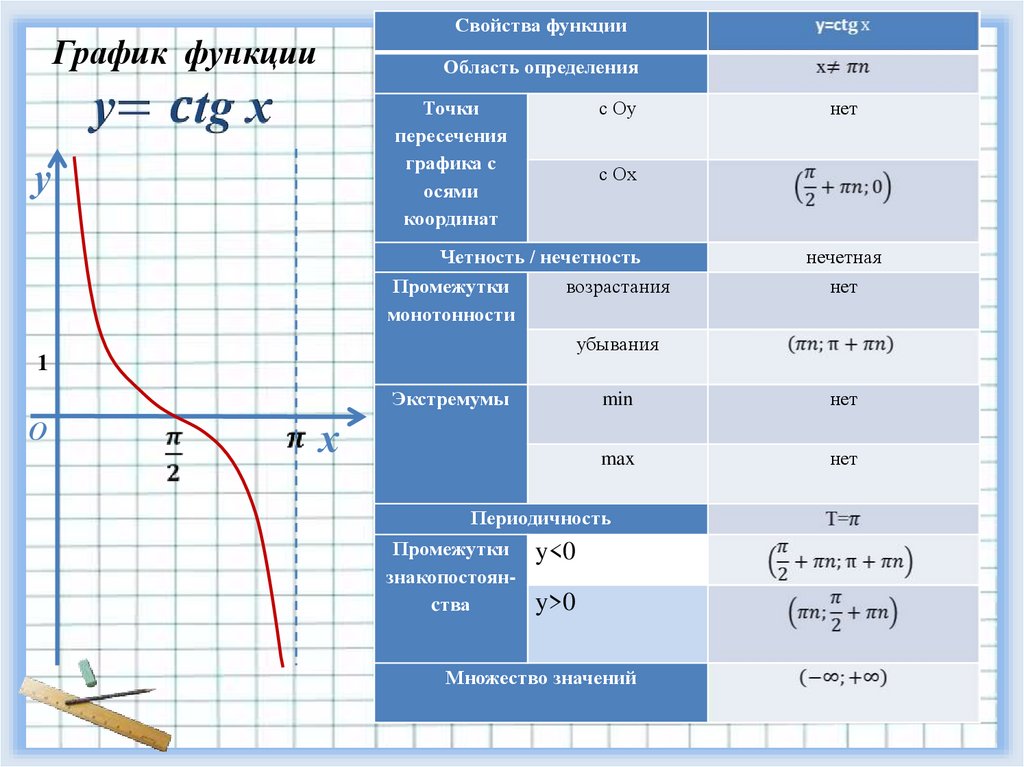
Основные свойства функции y=tgx: 1) Область определения функции: 2) Множеством значений функции: 3) Функция является нечетной, график симметричен относительно …
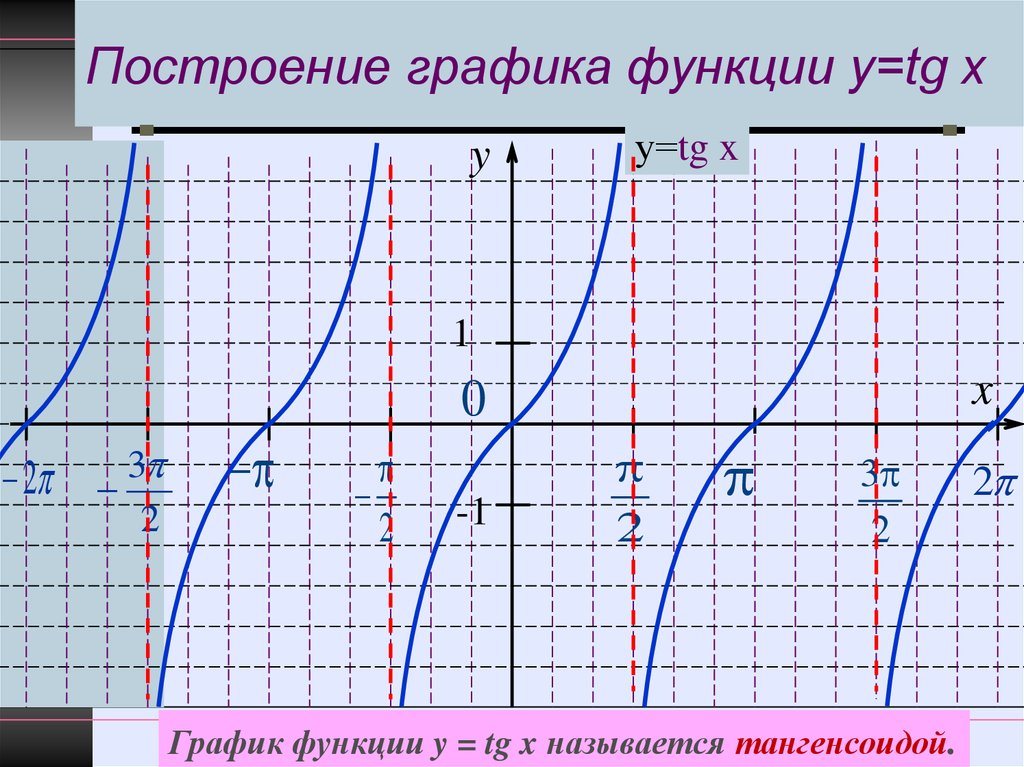
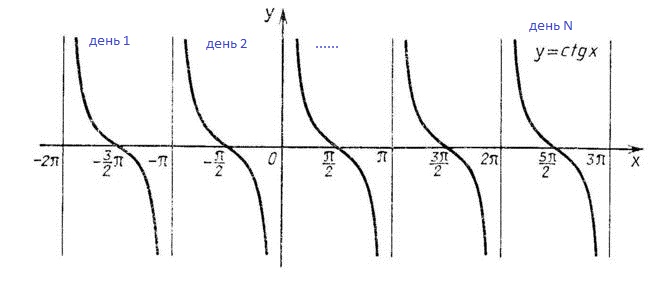Тангенсоида Свойства тригонометрических функций и их графики изучаются в курсе алгебры. Одна из тригонометрических функций Y=tgX.
Тангенсоида. Котангенсоида. Из истории возникновения тригонометрии
Рассмотреть свойства чётности, нечётности и периодичности тригонометрических функций. Применять полученные ранее знания общих свойств …
Как построить график функции y = tg x? Что такое тангенсоида? Какие свойства есть у функции y = tg x?
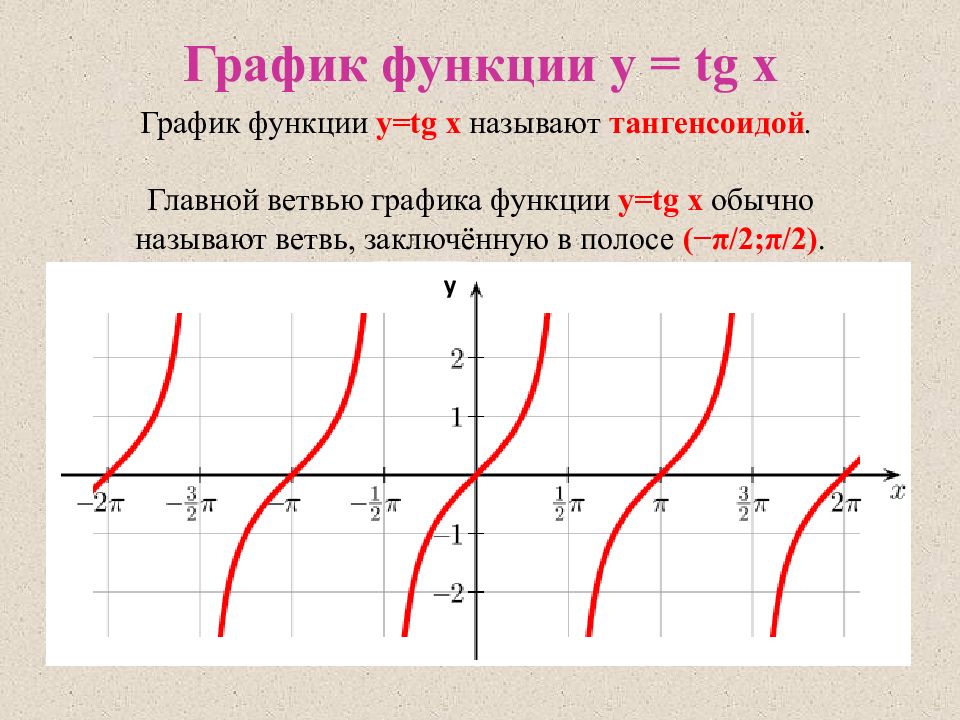
График y =tg x называют тангенцоидой. Часть тангенцоиды c \ (-\frac\pi2\lt x\lt \frac\pi2\) называют главной ветвью тангенцоиды. п.2. Свойства функции y =tg x . 1. Область …
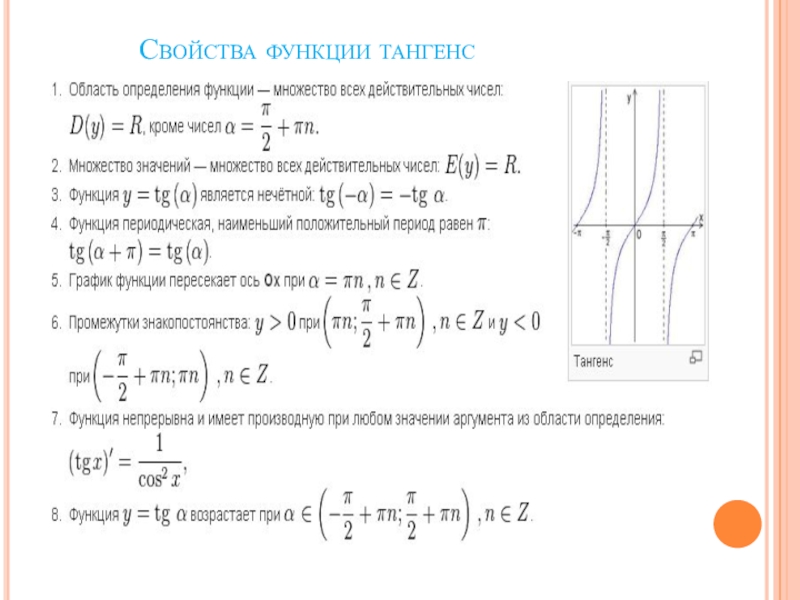
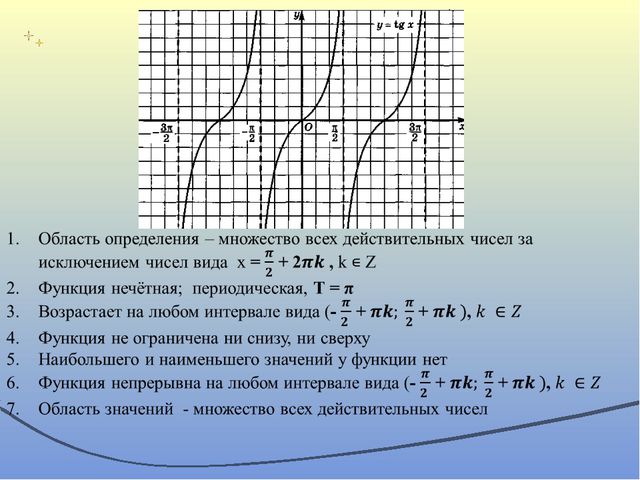
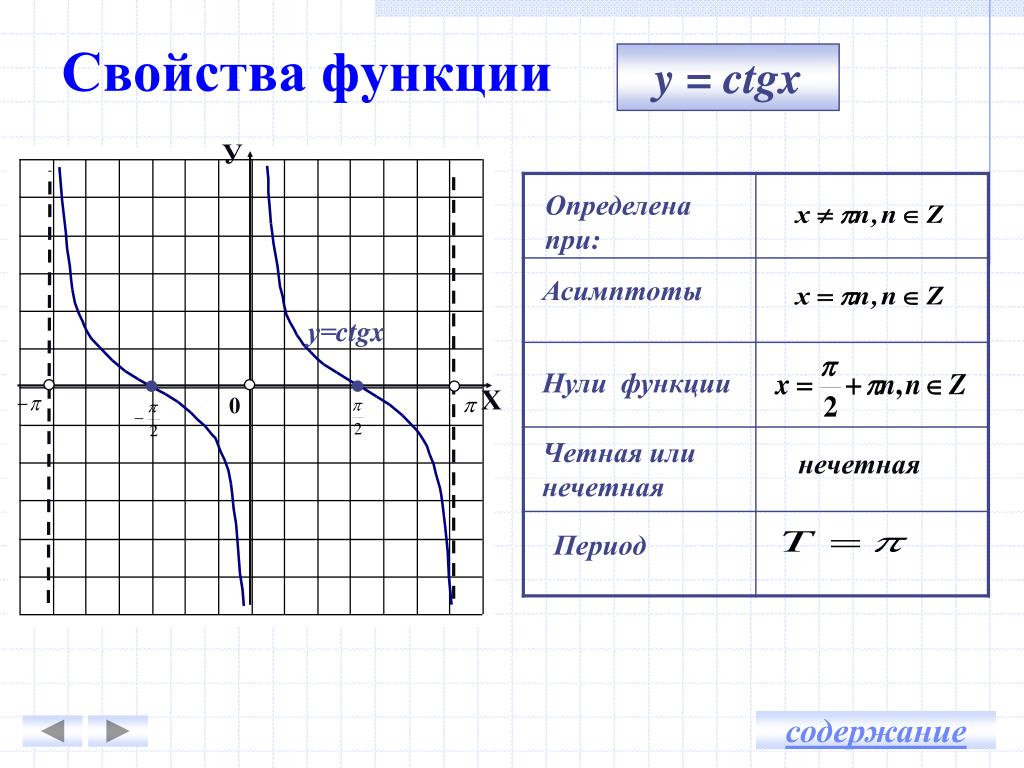Свойства функции тангенс. Свойство 1. Область определения функции тангенс – это множество R всех действительных чисел, кроме π/2 + π·n, где n ∈ Z (D (tg x)=R\ { π/2 + …
Еще по теме:
Еще по теме:
