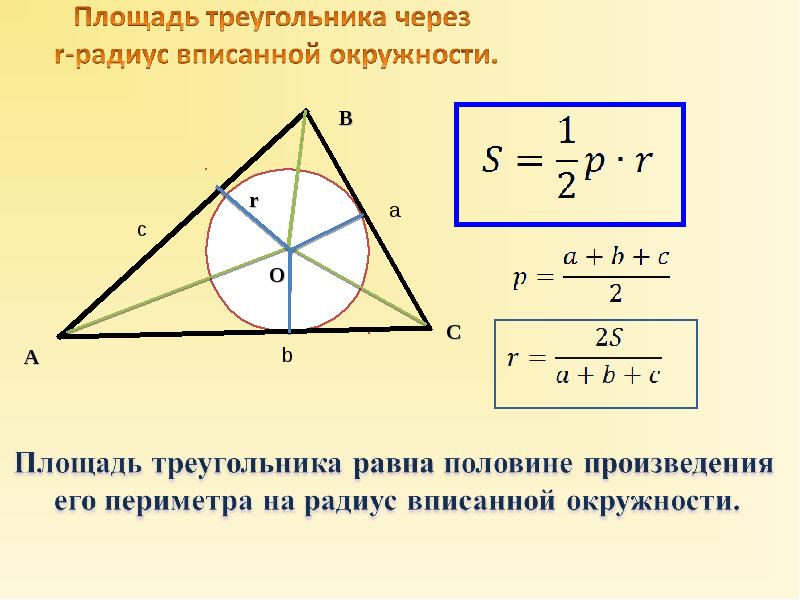
Рассмотрим теперь окружность, описанную около равностороннего треугольника. Она проходит через все три вершины треугольника, касаясь его сторон. …
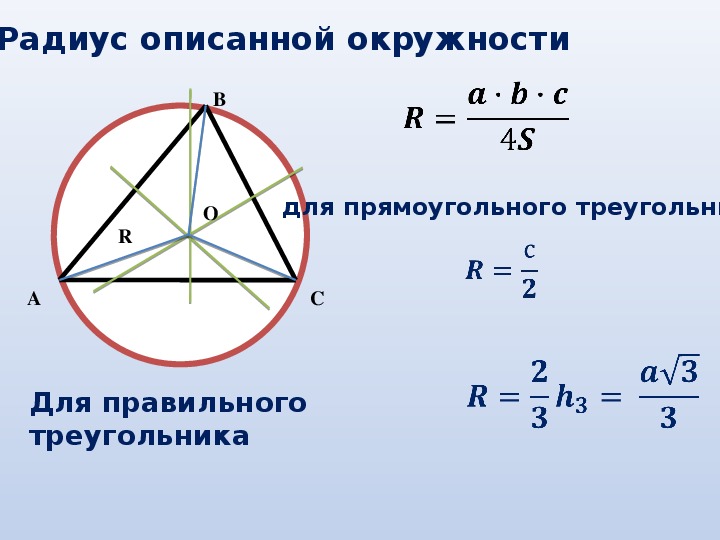
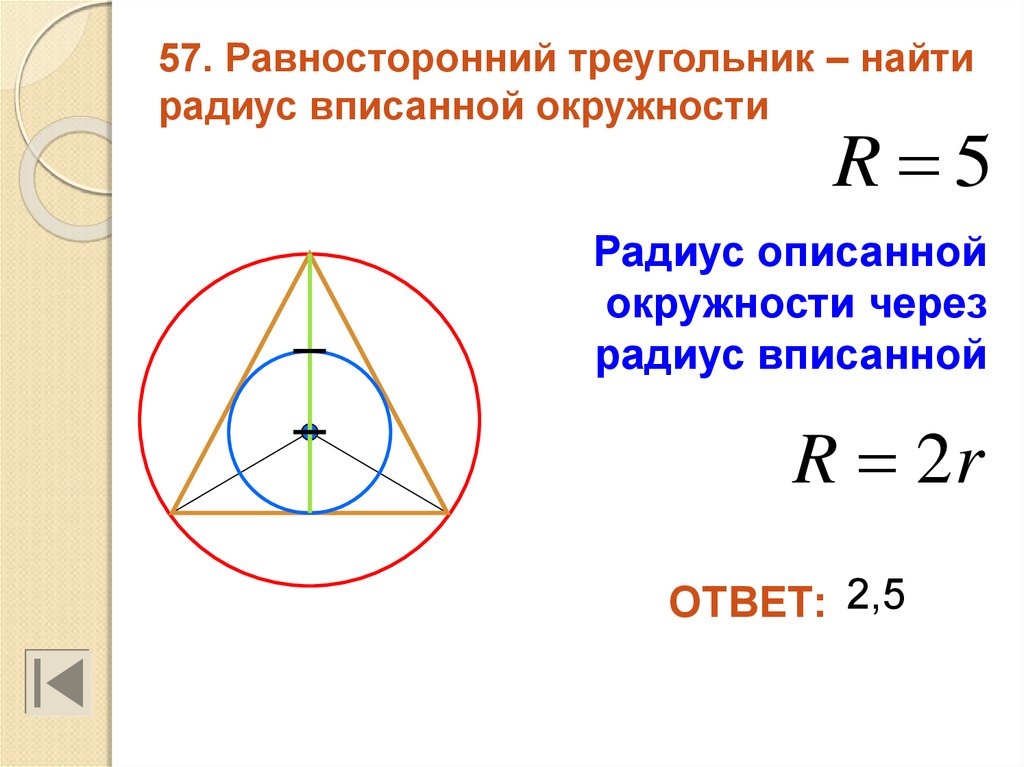
Формула для равностороннего треугольника Радиус описанной вокруг правильного треугольника окружности равен длине стороны, умноженной на корень квадратный из трех, деленный на три.
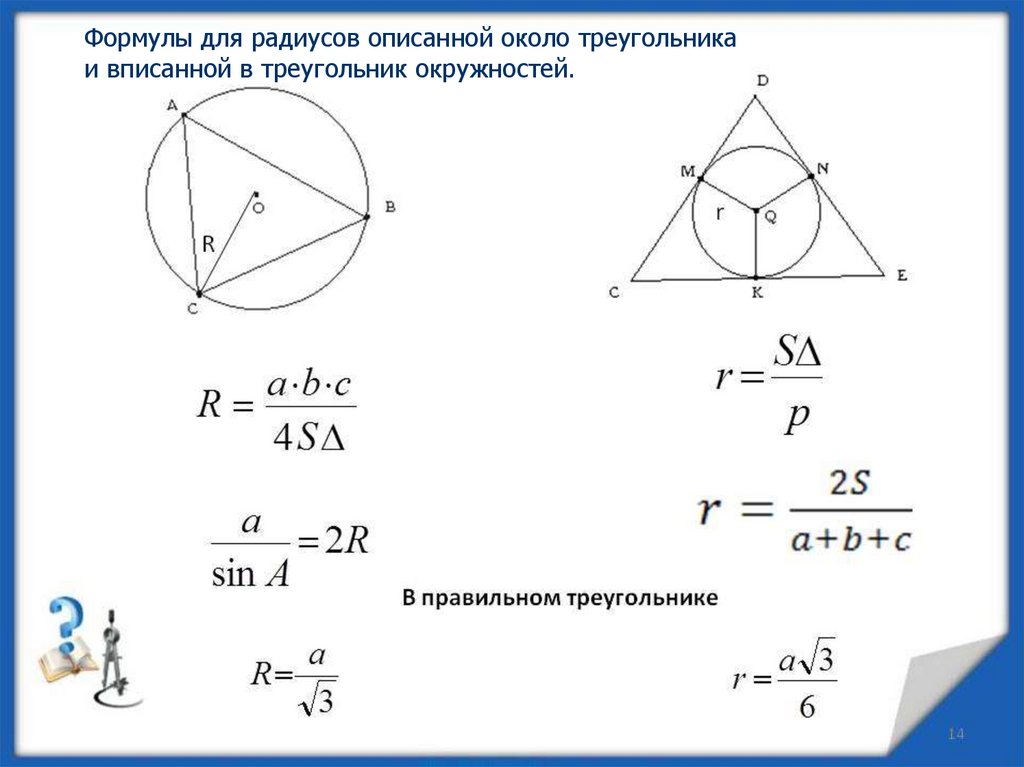
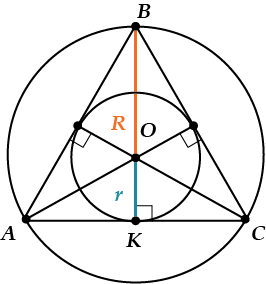- радиус описанной окружности, выраженный через сторону равностороннего треугольника, - радиус вписанной окружности, выраженный через радиус описанной окружности.
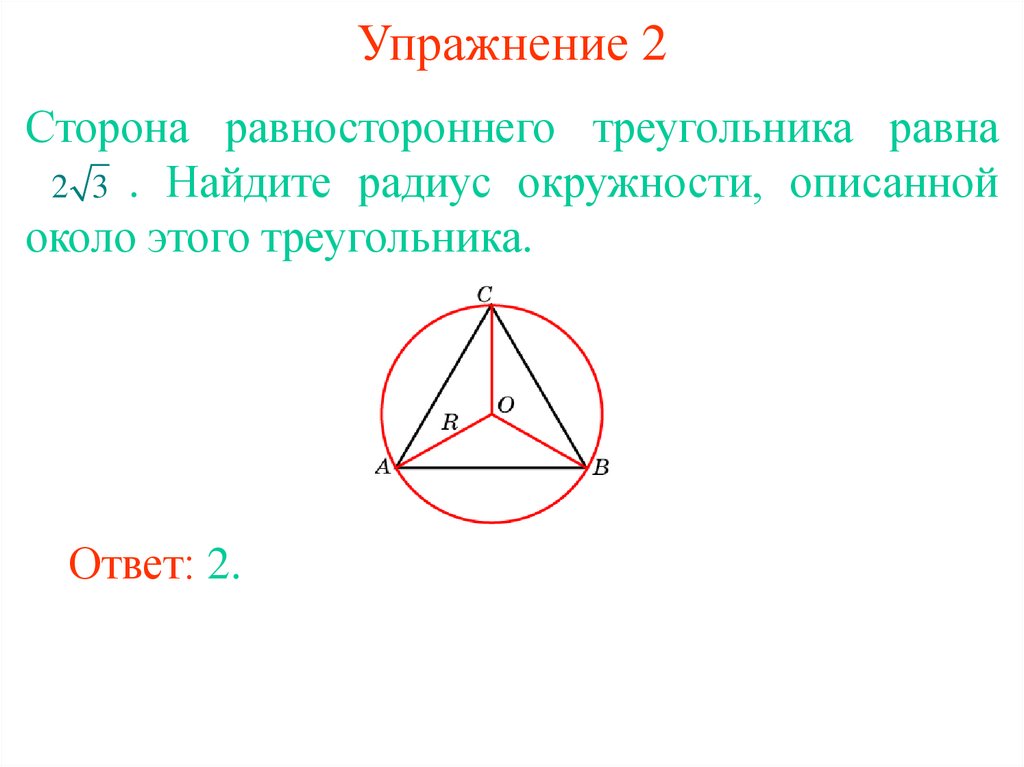
Сторона равностороннего треугольника равна радиусу описанной вокруг этого треугольника окружности, умноженному на квадратный корень из трех. Сторона равностороннего …
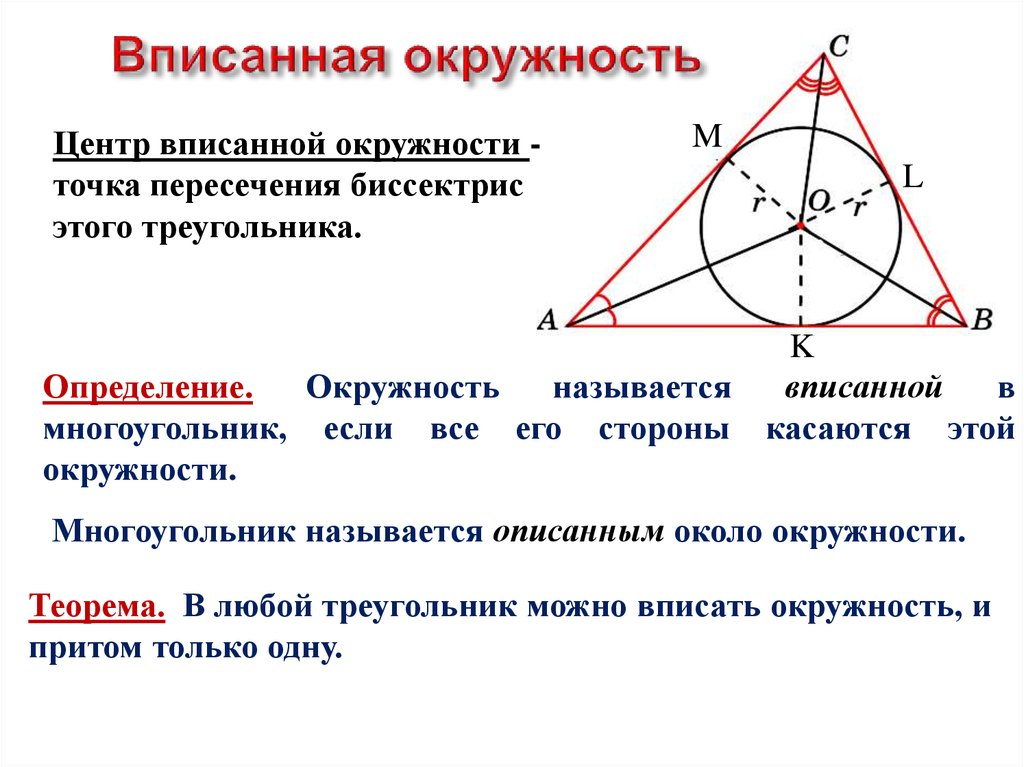
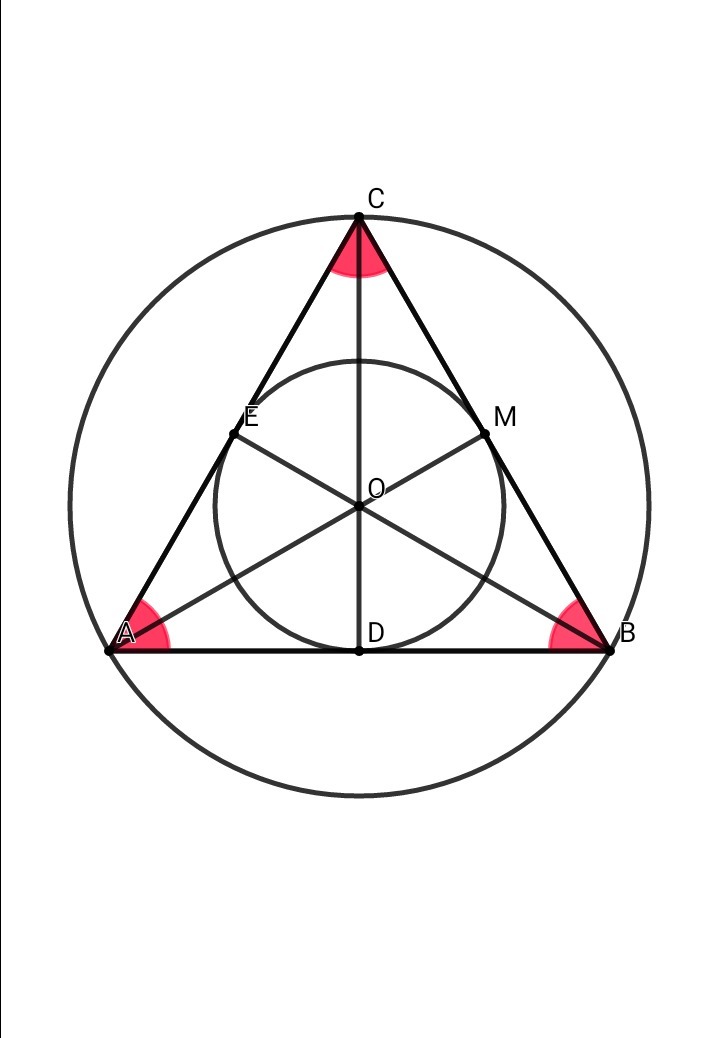
Правильный треугольник, описанный около окружности, имеет точки касания с окружность, в серединах сторон. Свойство 20. Равнобедренный, прямоугольный, равносторонний
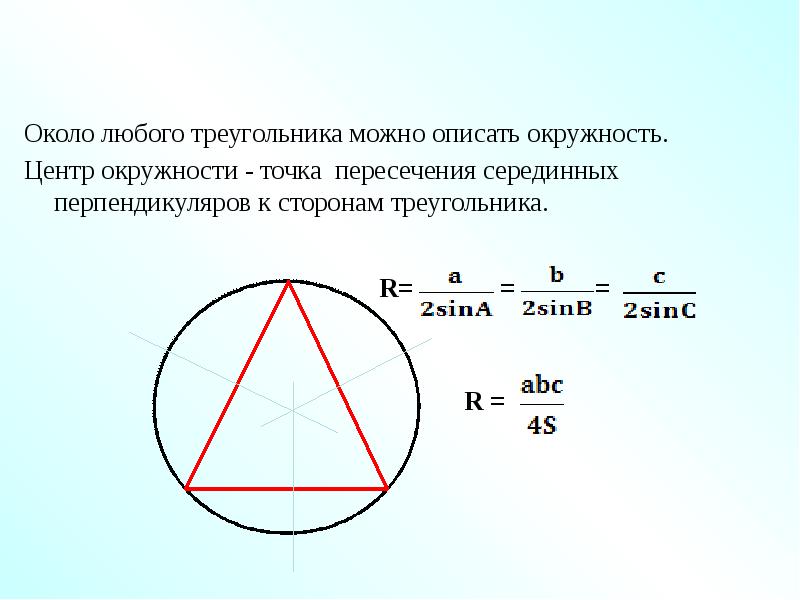
Радиус окружности, описанной около произвольного треугольника, вычисляется по формуле: , где a, b, c — стороны треугольника, S — площадь треугольника. Для равностороннего …
Описанный треугольник — это треугольник, который может быть вписан в окружность таким образом, что каждая сторона треугольника будет являться хордой …
В окружность вписан треугольник \(klm\) таким образом, что одна сторона треугольника проходит через центр окружности.
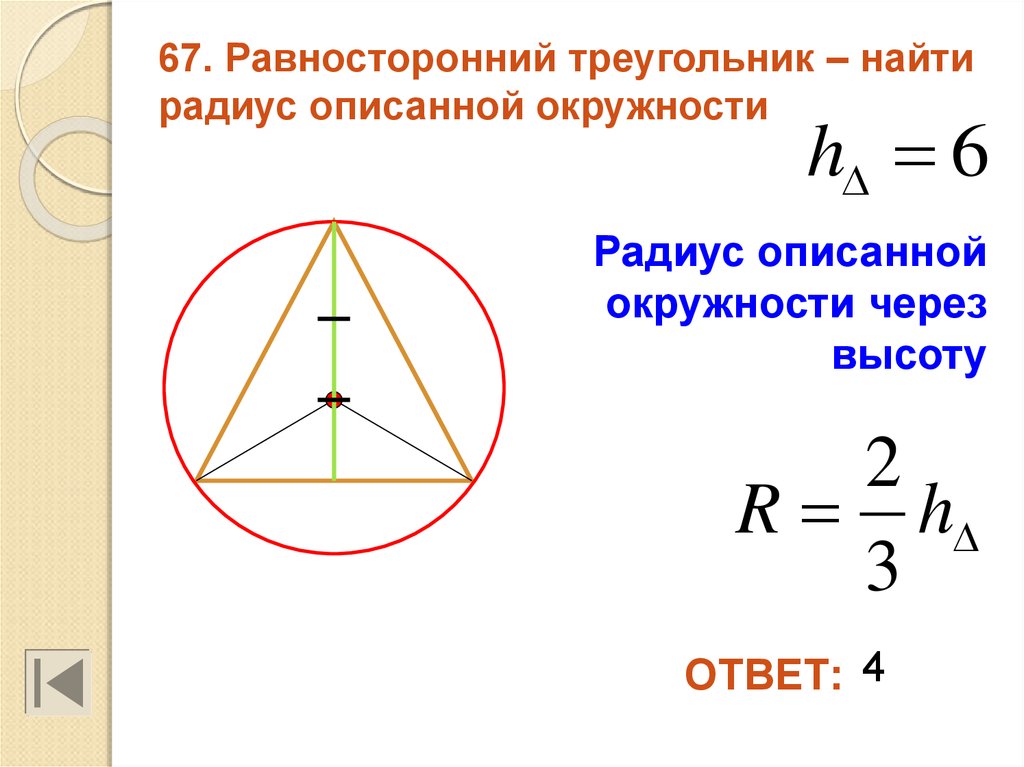Треугольник, вписанный в окружность - это треугольник, который находится внутри окружности и соприкасается с ней всеми тремя вершинами. Свойства, формулы, примеры треугольника.
Калькулятор - вычислить, найти радиус описанной окружности равностороннего треугольника по стороне. Зная сторону равностороннего треугольника, …
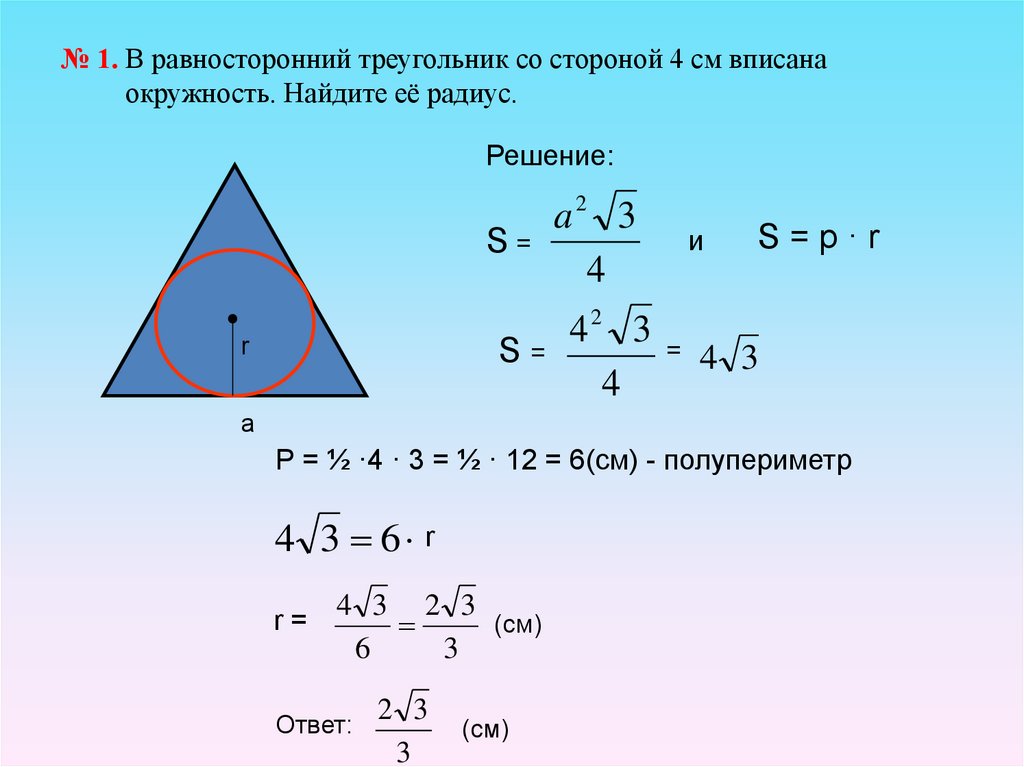
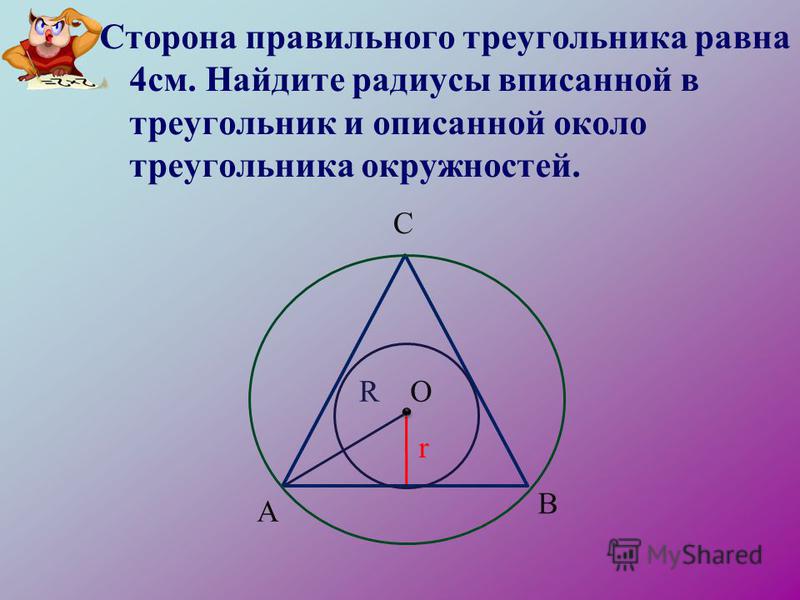
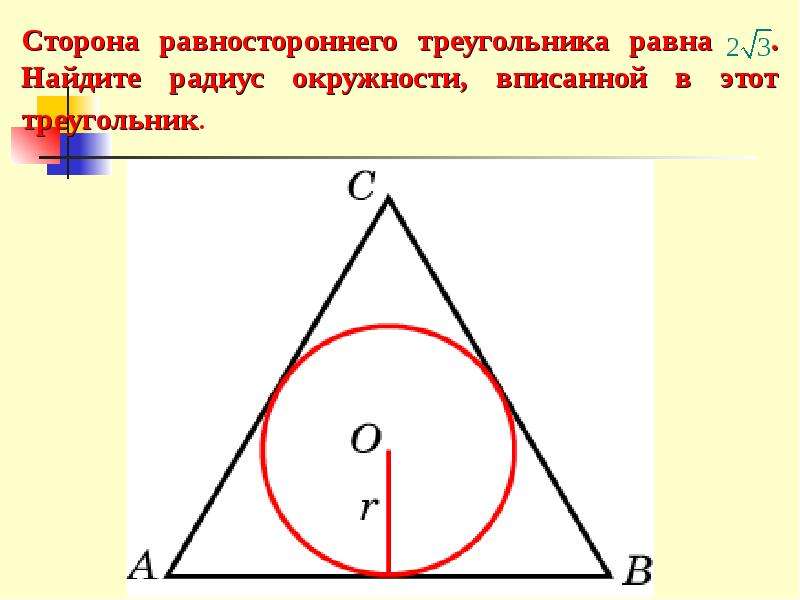
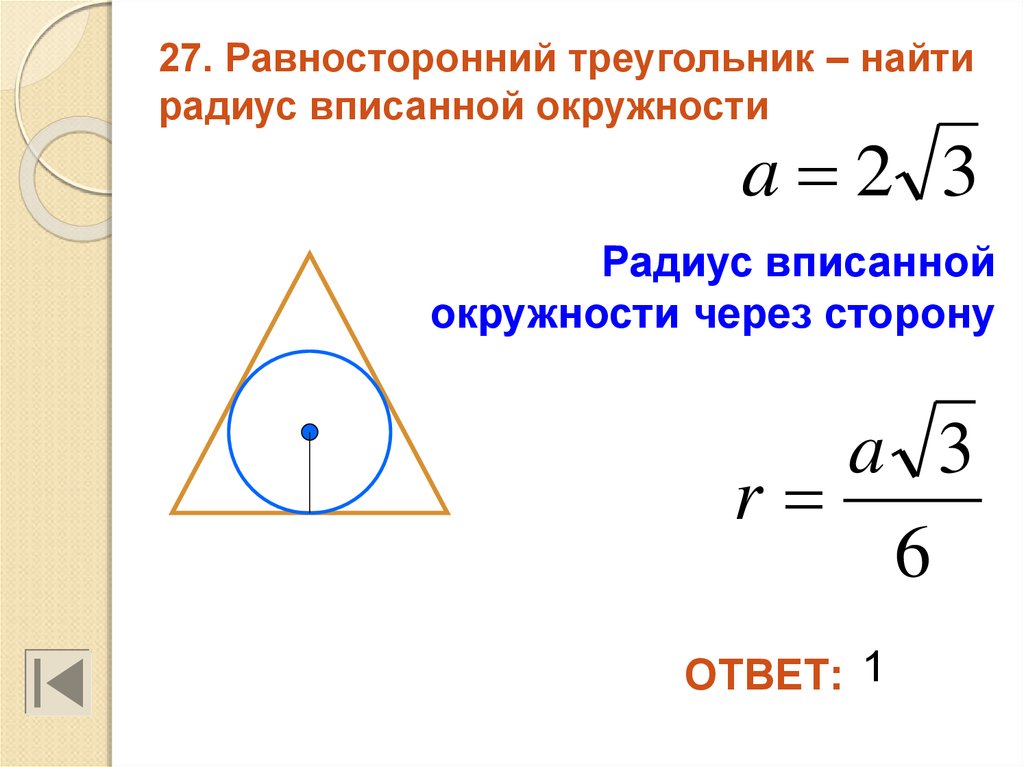
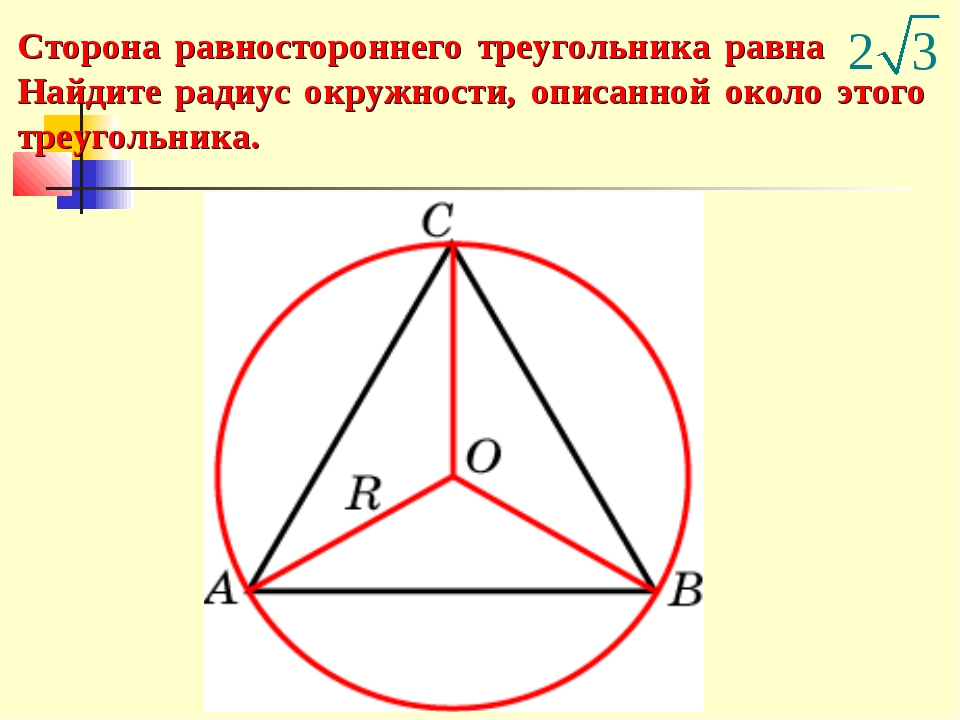Вписанная окружность в равносторонний треугольник и свойства его сторон. Рассмотрим правильный треугольник АВС со стороной а (AB=BC=AB=a), в который вписана …
Описанный равносторонний треугольник. Скачай курс в приложении Перейти в приложение Открыть мобильную версию сайта Каталог Моё.
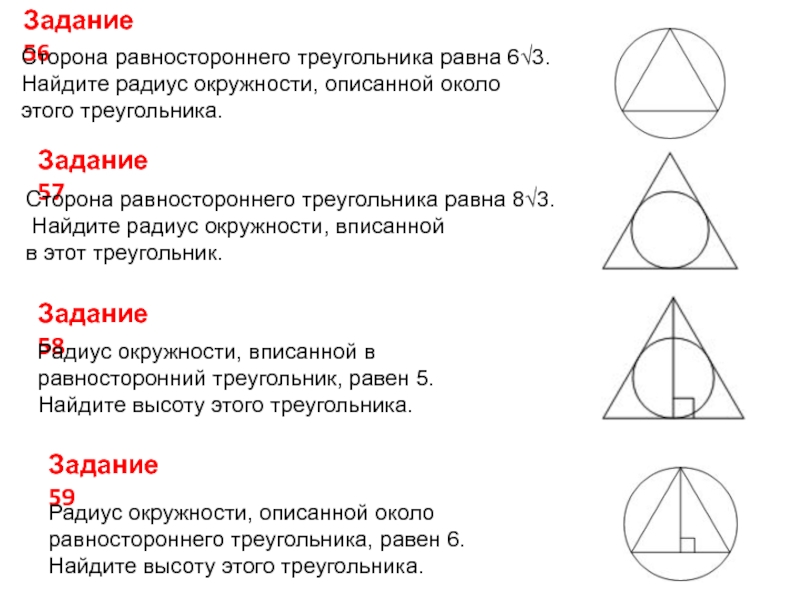
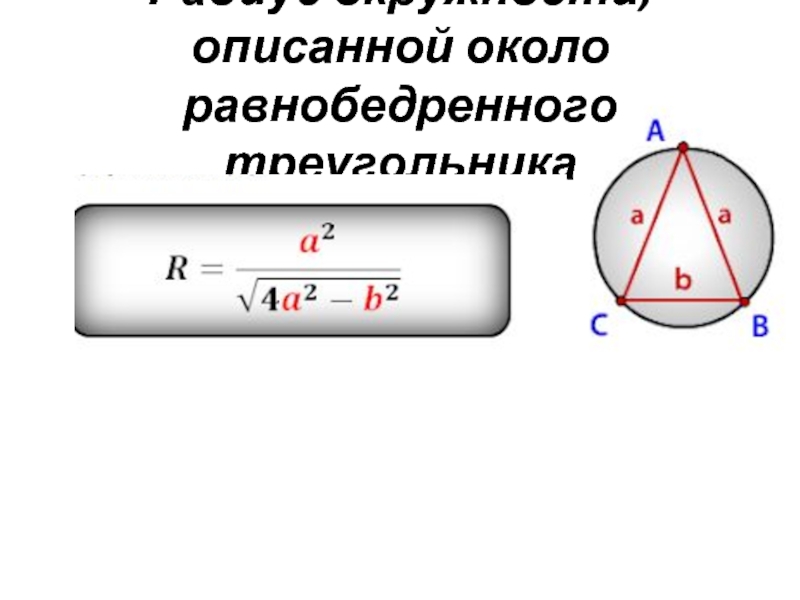Приведены пояснения и численные примеры применения формул для расчета радиуса описанной окружности прямоугольного, равнобедренного и других …
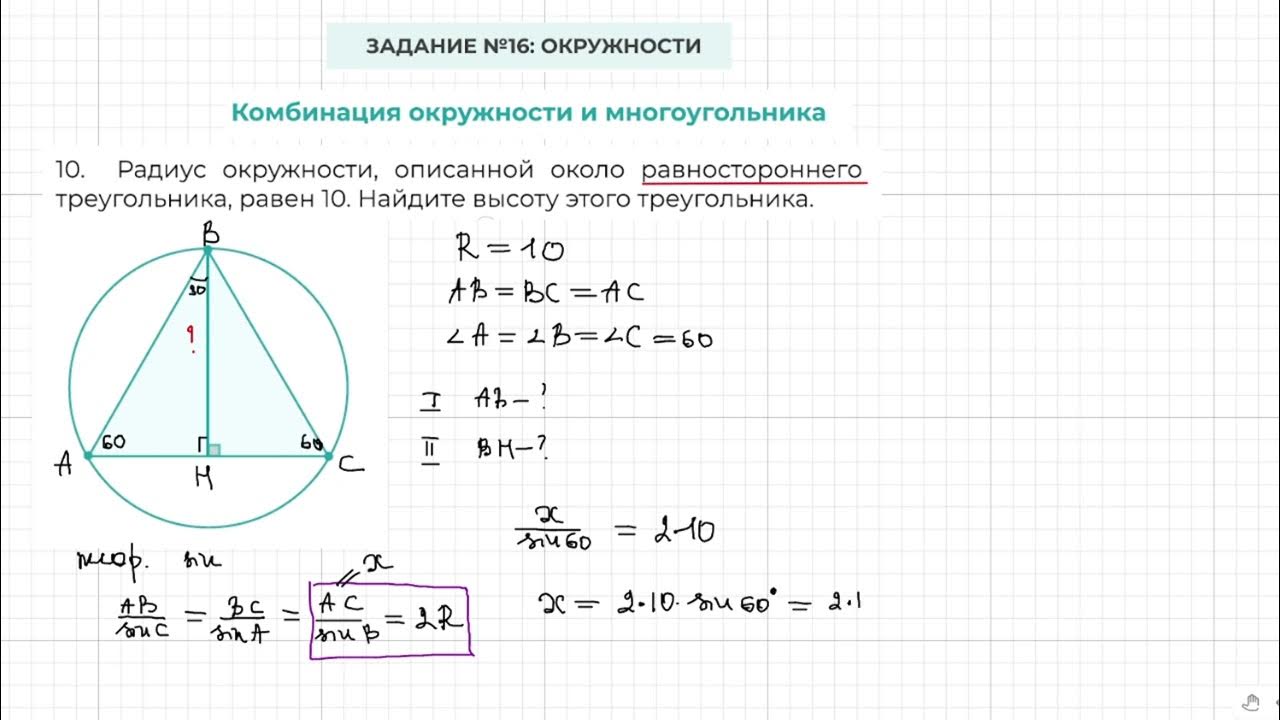
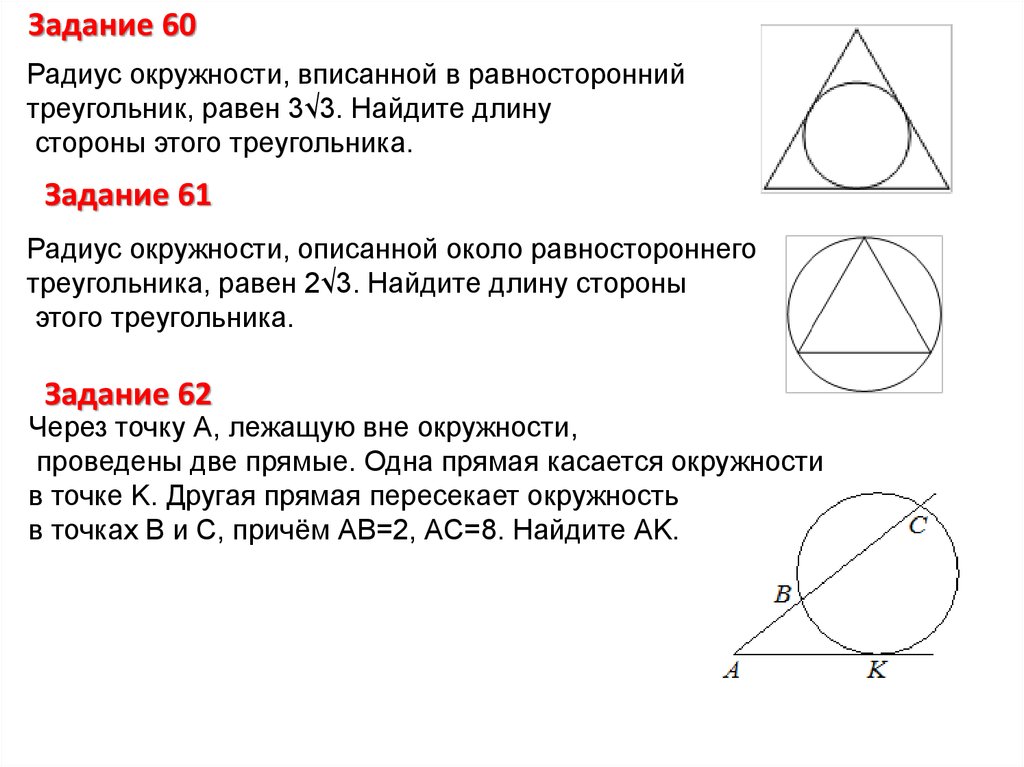
Дано: равносторонний треугольник, вписанный в окружность. Радиус окружности равен 14 см.
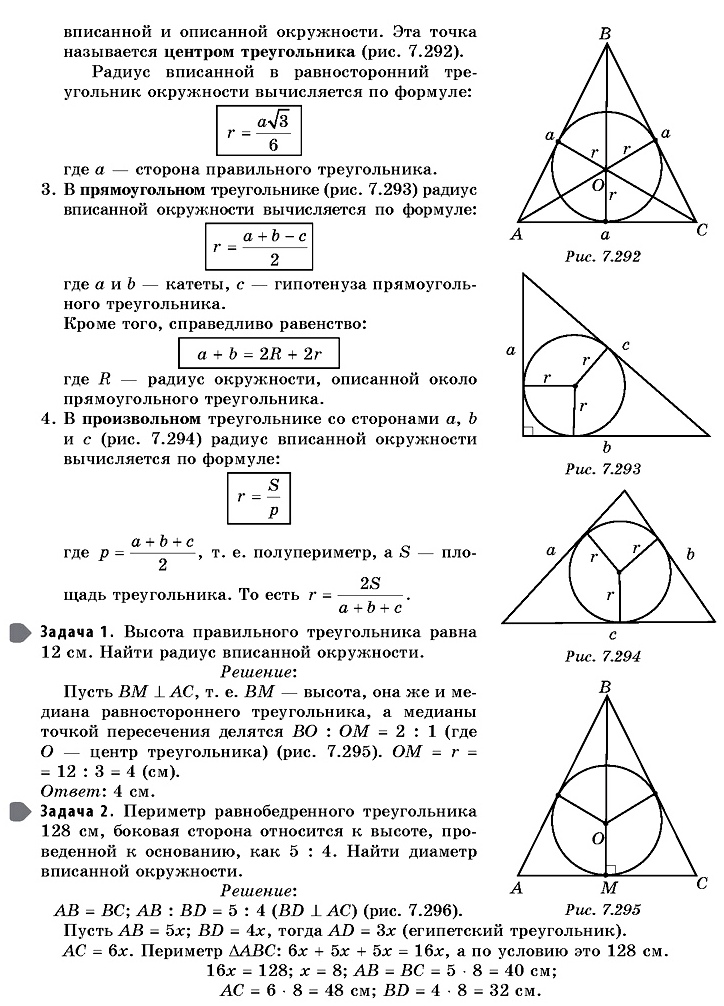
Центр вписанной в равносторонний треугольник окружности лежит на высоте BH и делит ее в отношении 2:1, считая от вершины B. В задании нам дана величина радиуса OH=r=6, …
Еще по теме:
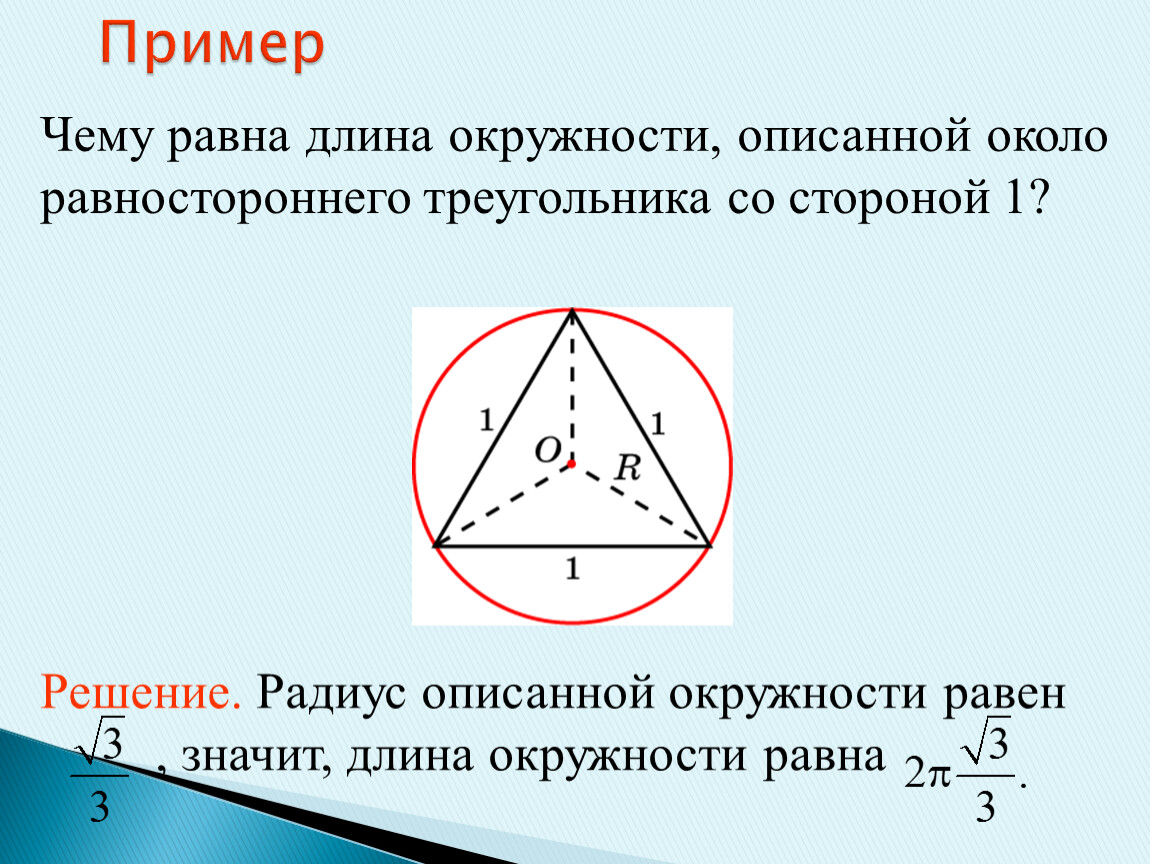
Еще по теме:
