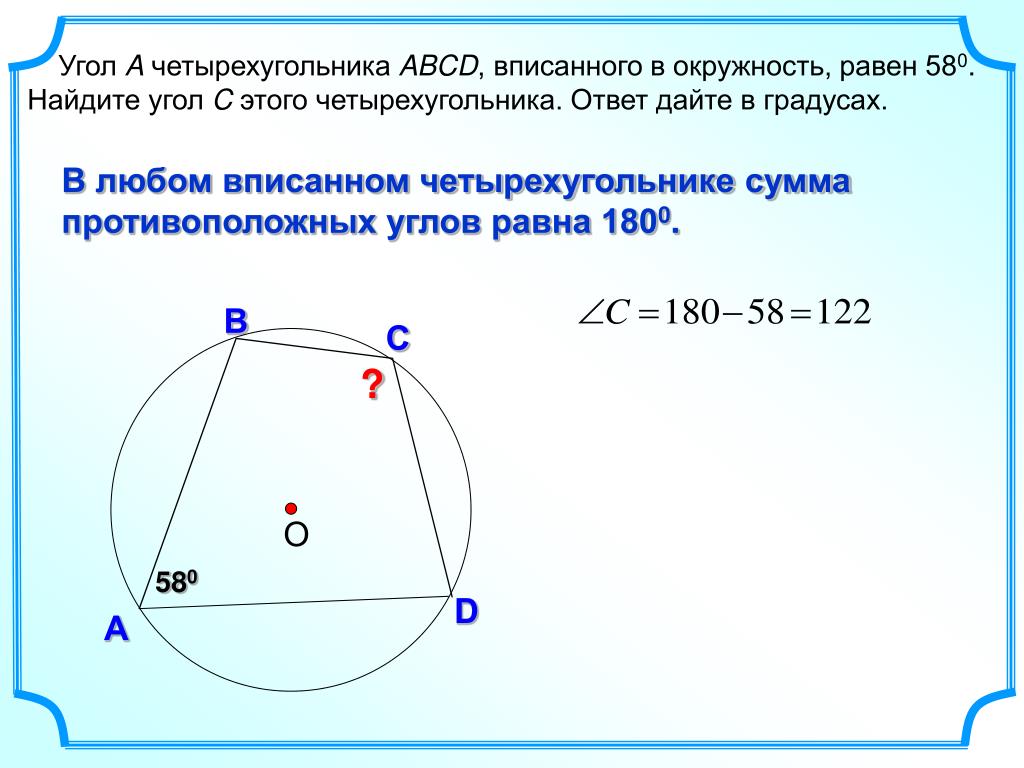
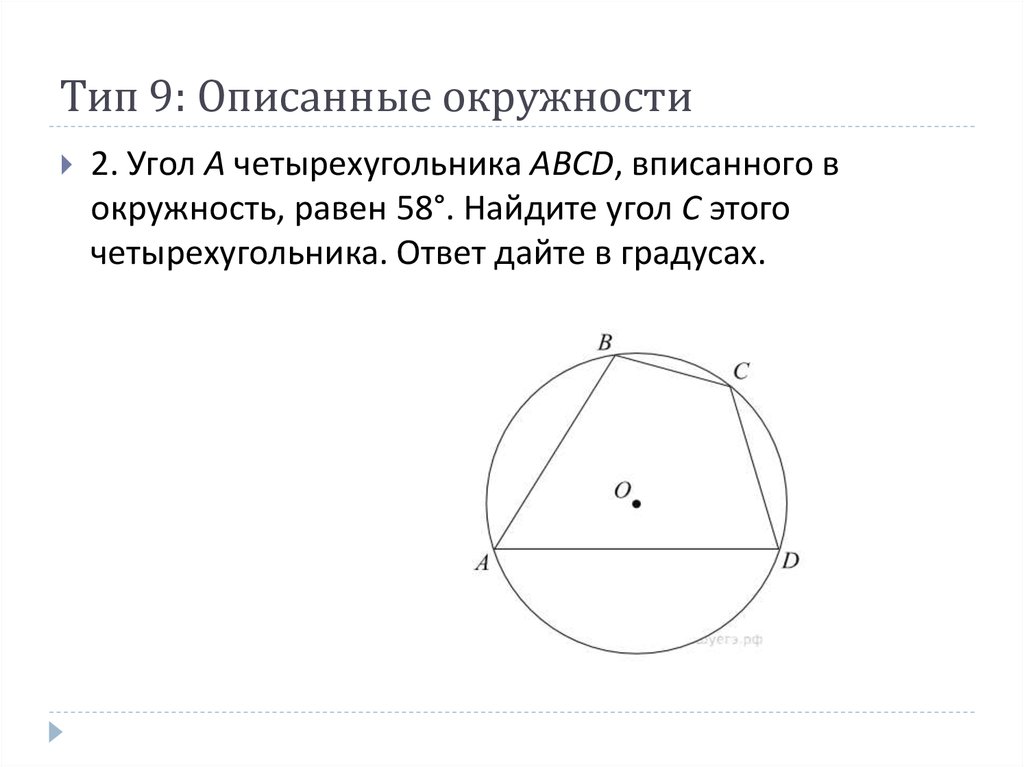
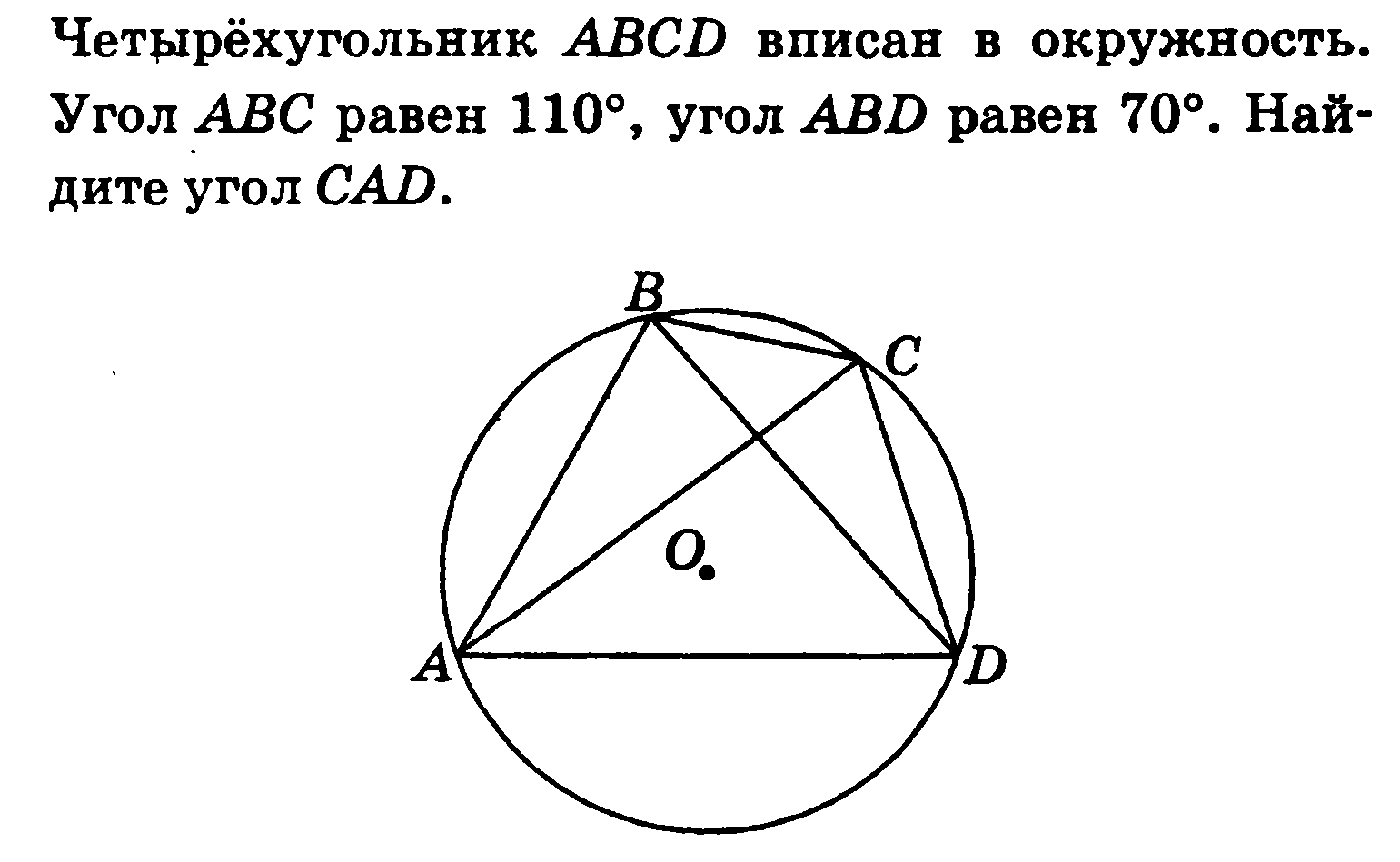
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности. Эта окружность будет называться описанной вокруг четырехугольника. …
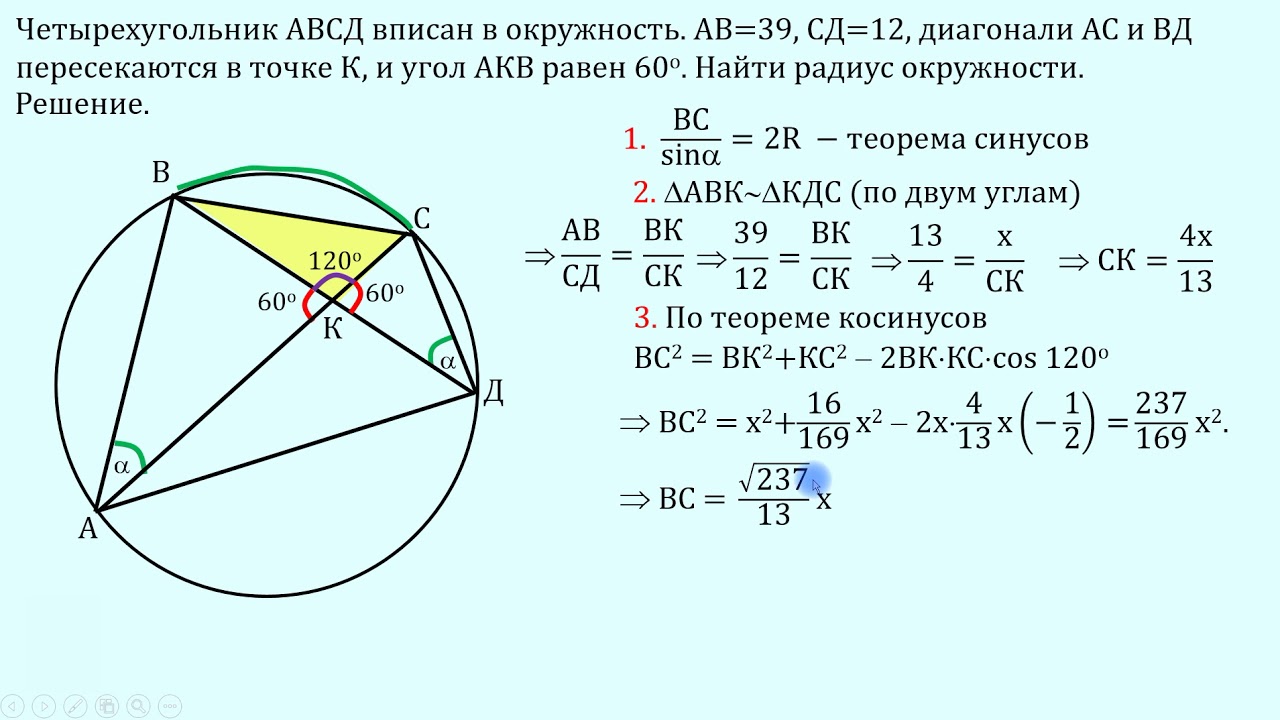
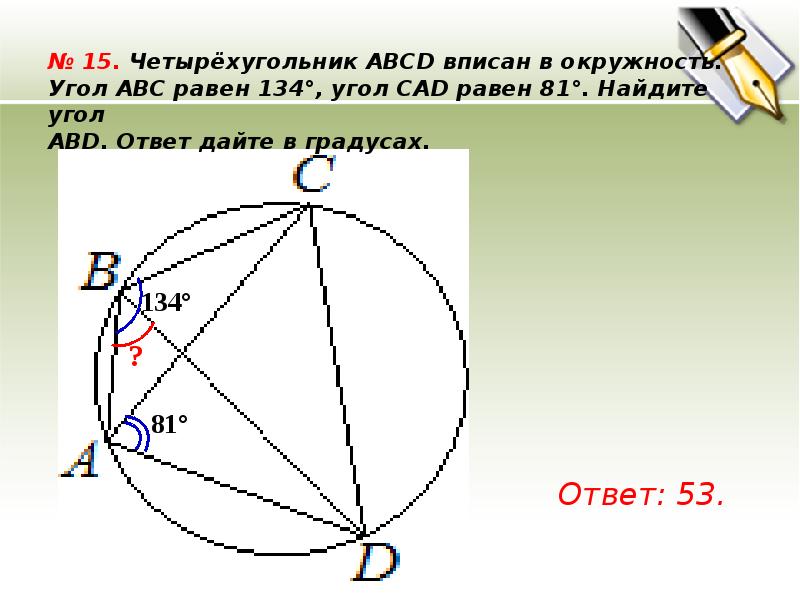
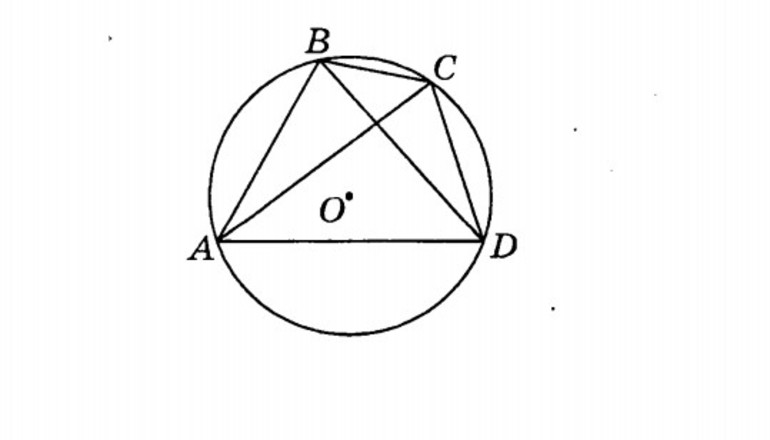
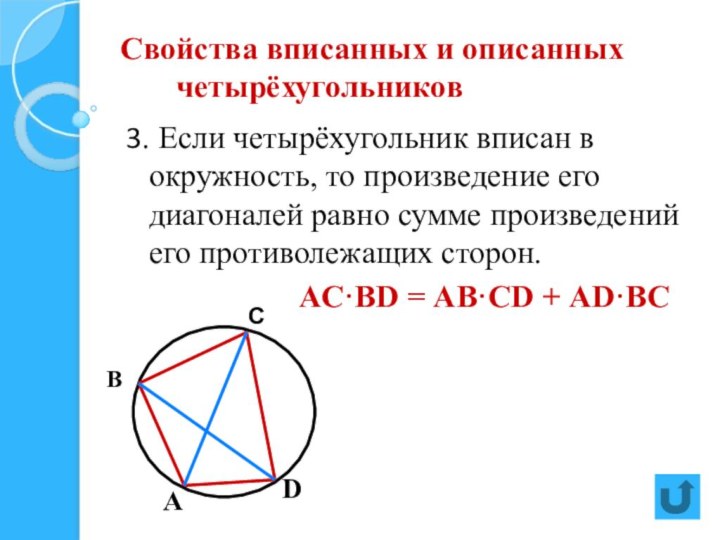
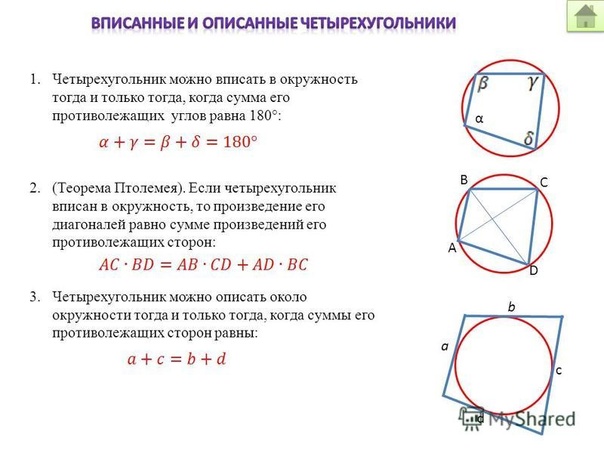Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах. Спрятать решение. Решение. Угол ABC — …
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°. ДОКАЗАТЕЛЬСТВО. Угол abc является вписанным углом, опирающимся на дугу adc (рис.1).
Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности. Центр окружности, описанной около четырехугольника — точка пересечения серединных перпендикуляров, …
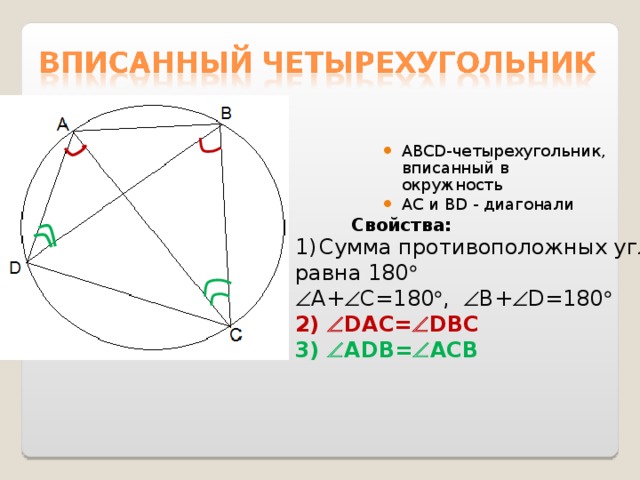
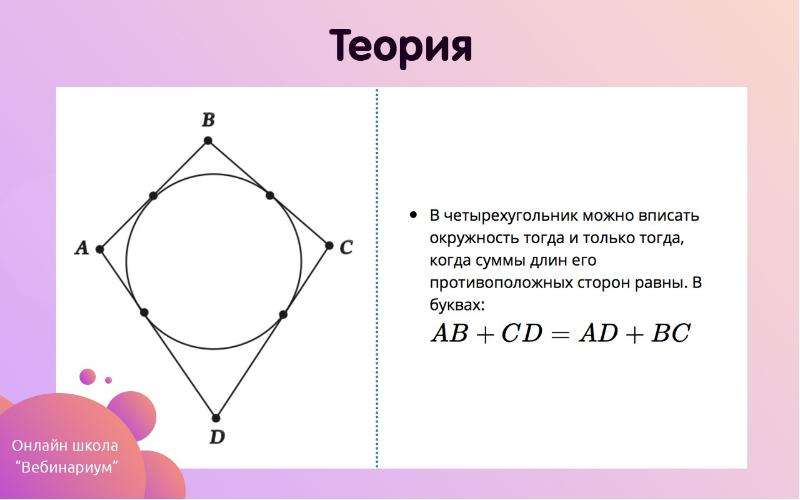
Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его …
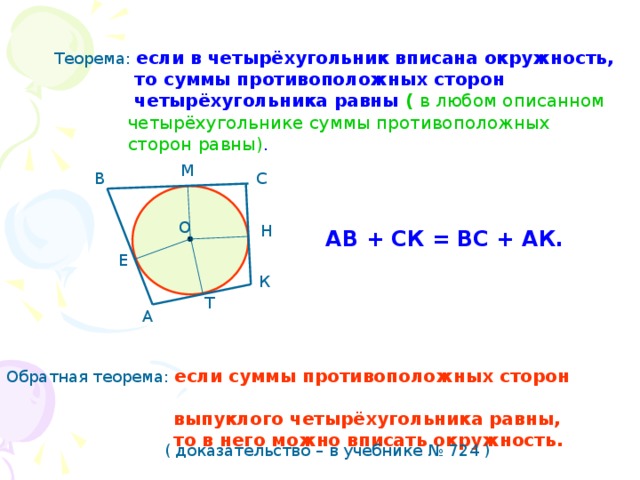
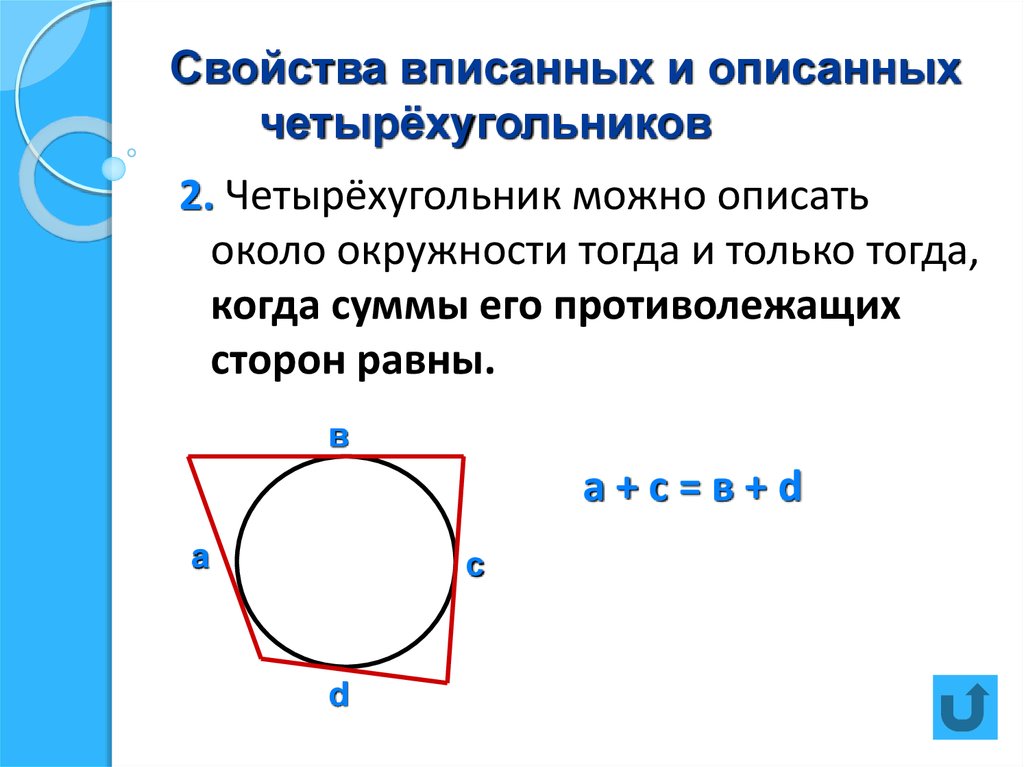
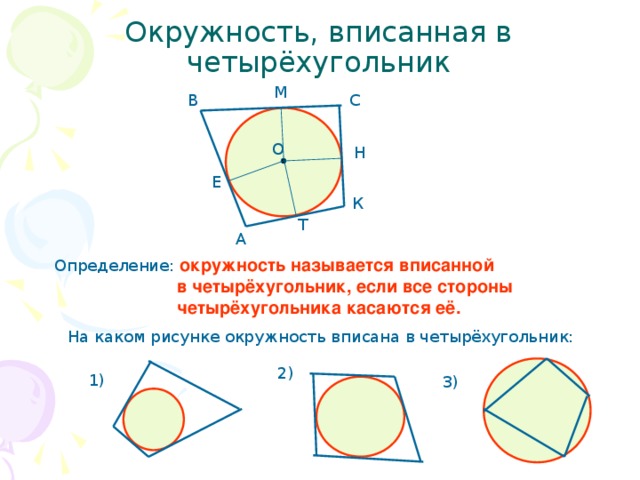
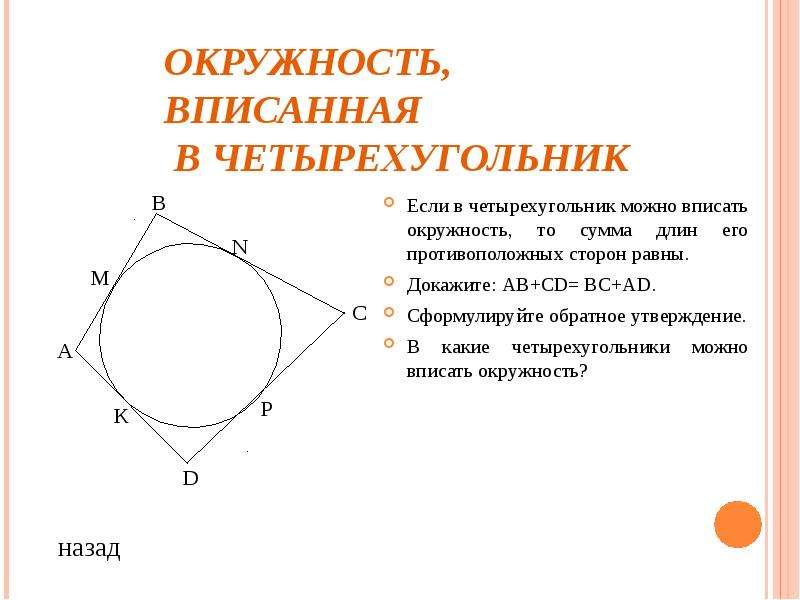
Окружность называют вписанным в четырехугольник, если окружность касается всех сторон четырехугольника. На рисунке 1 окружность вписан в четырехугольник ABCD. В этом случае говорят также, что …
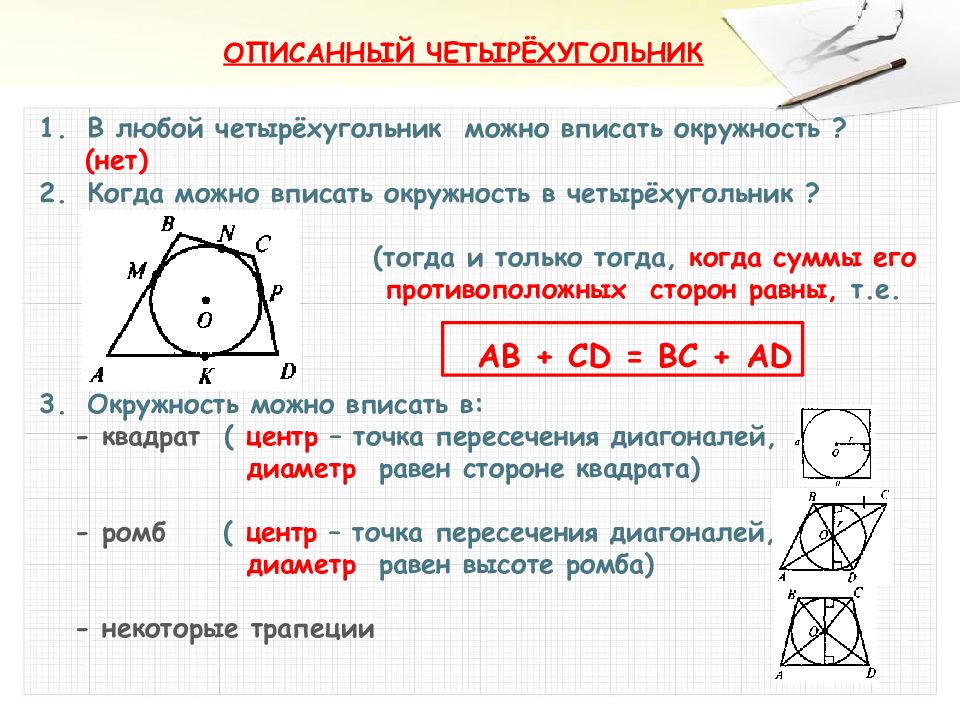Четырехугольник называют вписанным в окружность, если все вершины четырехугольника лежат на окружности. На рисунке 1 четырехугольник ABCD вписан в окружность.
Вписанный четырехугольник – это четырехугольник вокруг которого описана окружность (четырехугольник, который вписан в окружность).
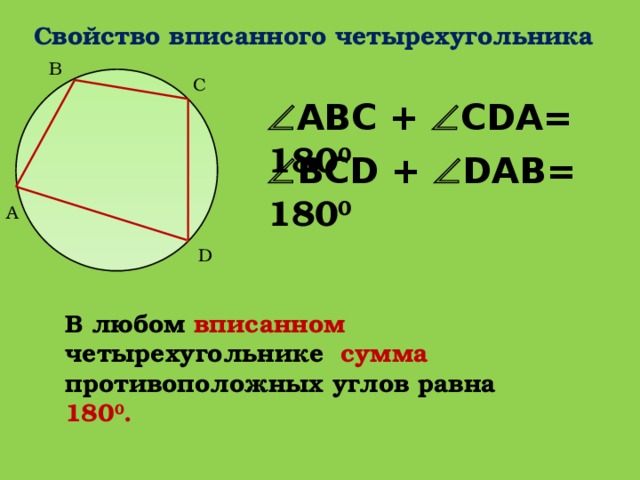
Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что < A + < C = 180º и < B + < D = 180º.
Определение. Четырехугольник называется вписанным в окружность, если все вершины четырехугольника лежат на окружности. Четырехугольник ABCD — вписанный в …
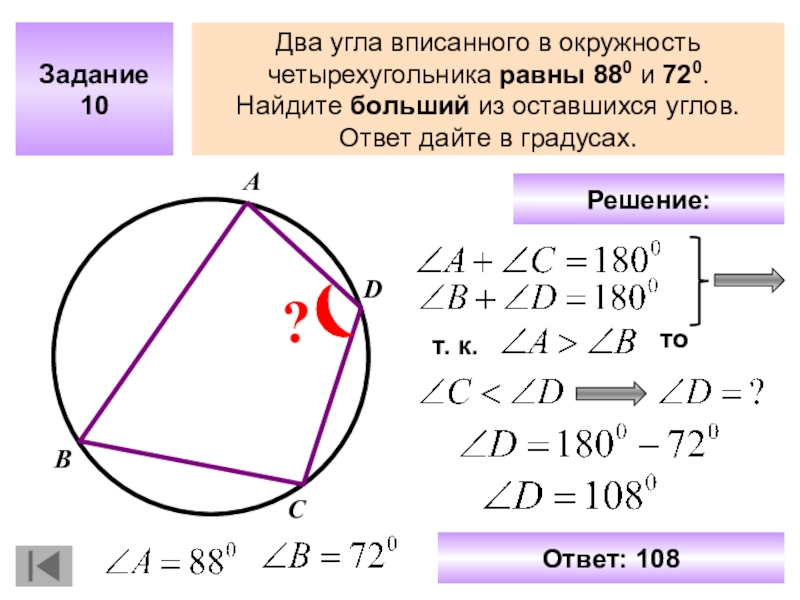
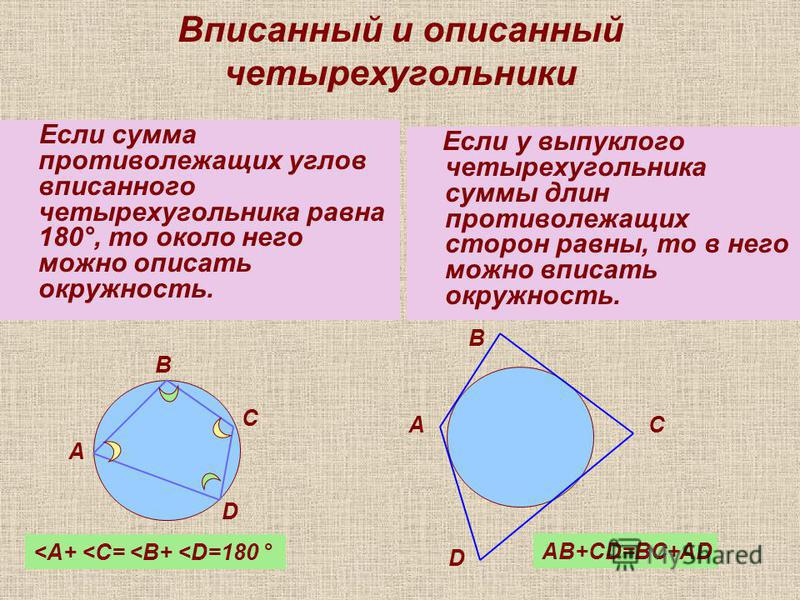
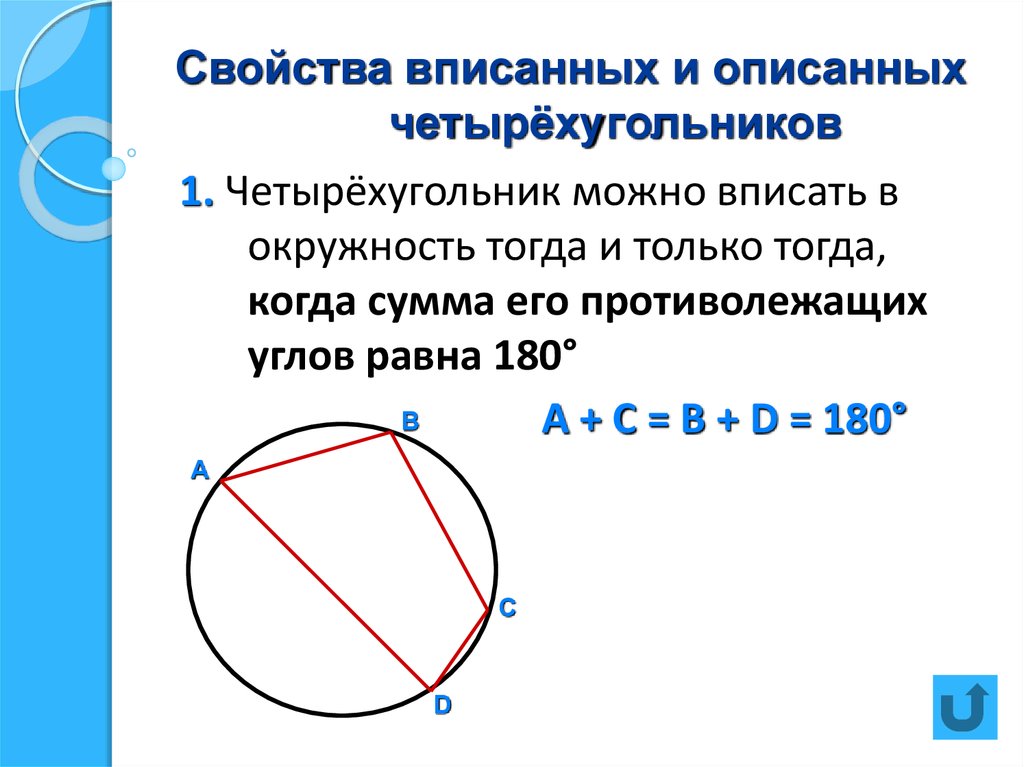
Какой-либо четырехугольник может быть вписан в некую окружность при условии, что его противолежащие углы в сумме дают 180°.
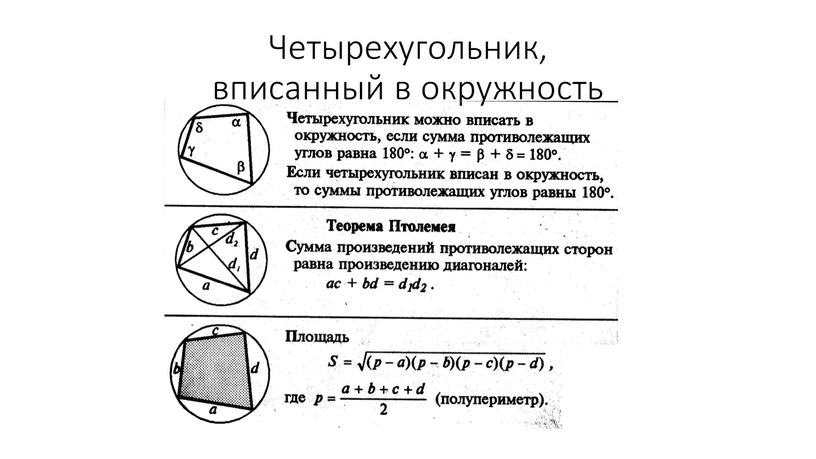
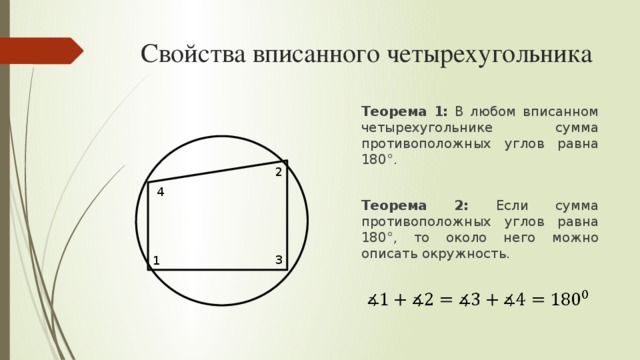
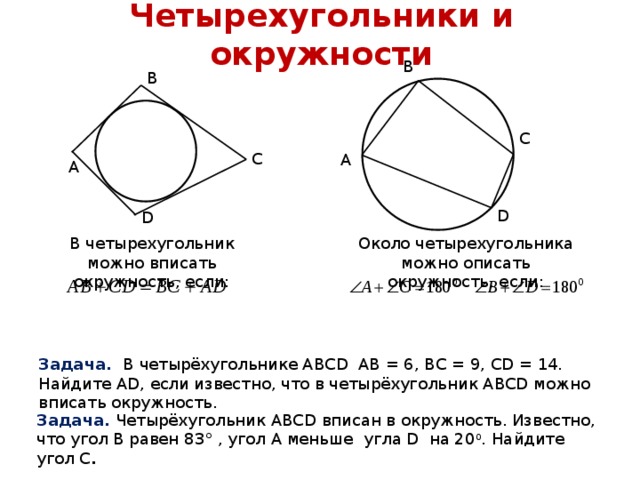Если четырехугольник вписан в окружность, то суммы его противоположных углов равны 180°: Теорема о вписанном четырехугольнике. Доказательство теоремы о вписанном …
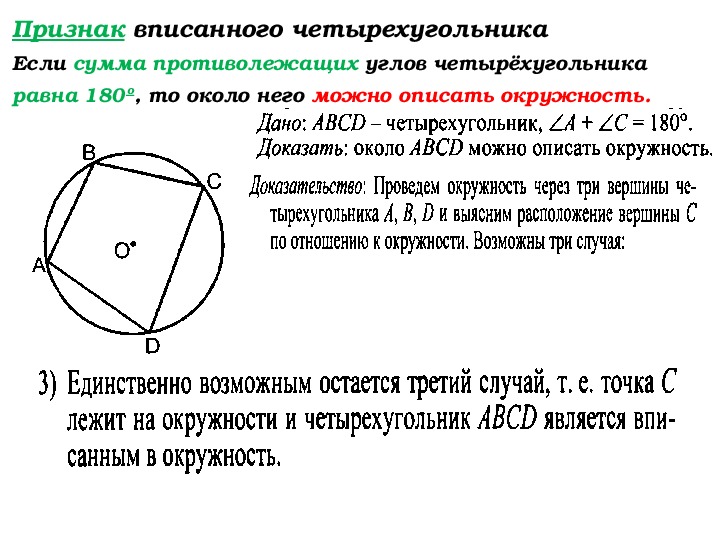
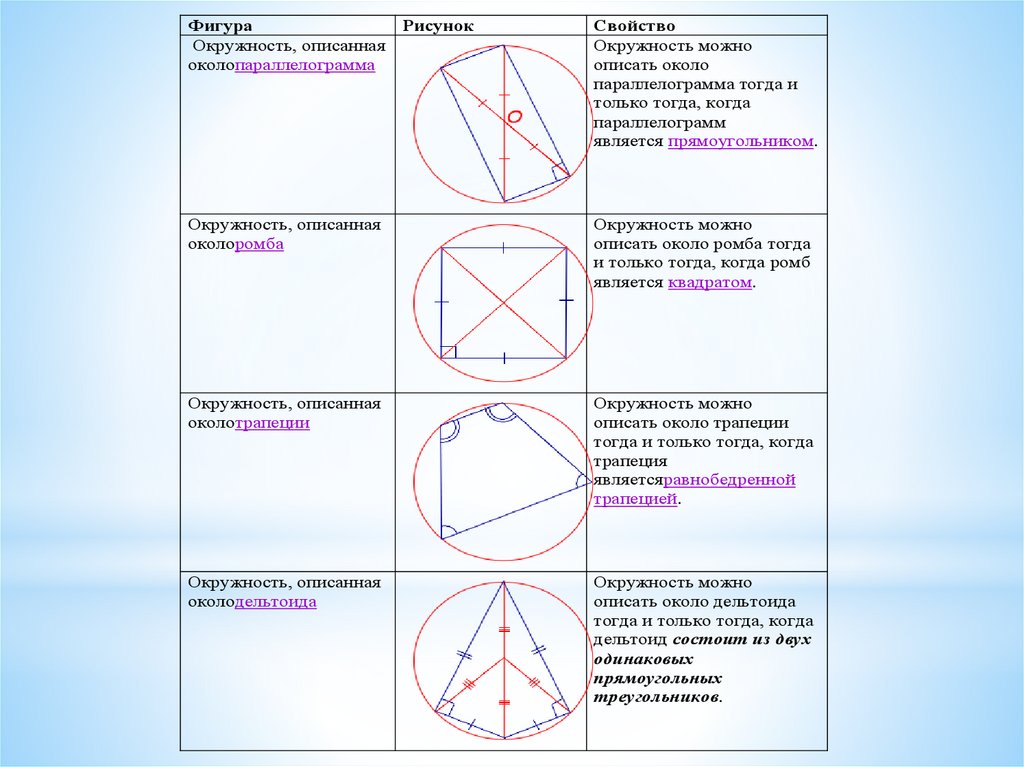В результате построения получим четырехугольник АВСn, который вписан в окружность. По теореме о вписанном четырехугольнике, суммы его противоположных углов будут равны …
Вписанный четырехугольник — коротко о главном. Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна 180∘. и наоборот: …
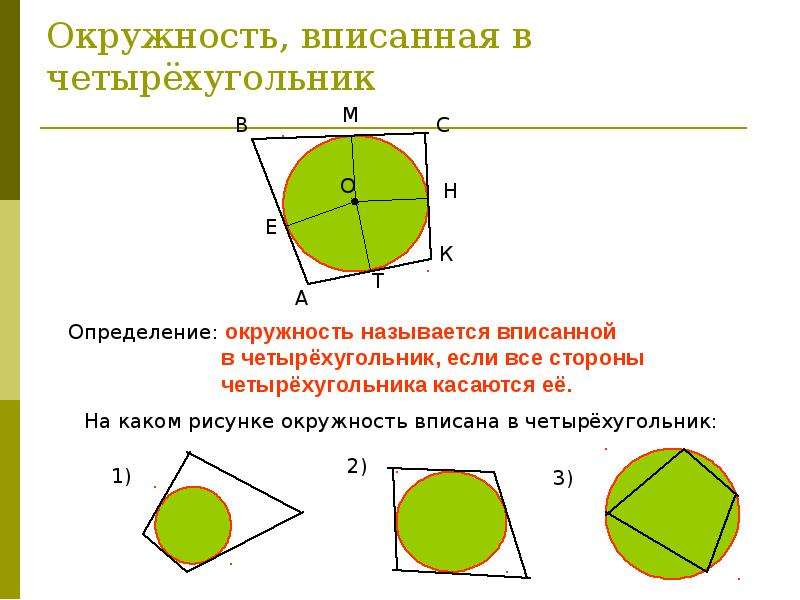
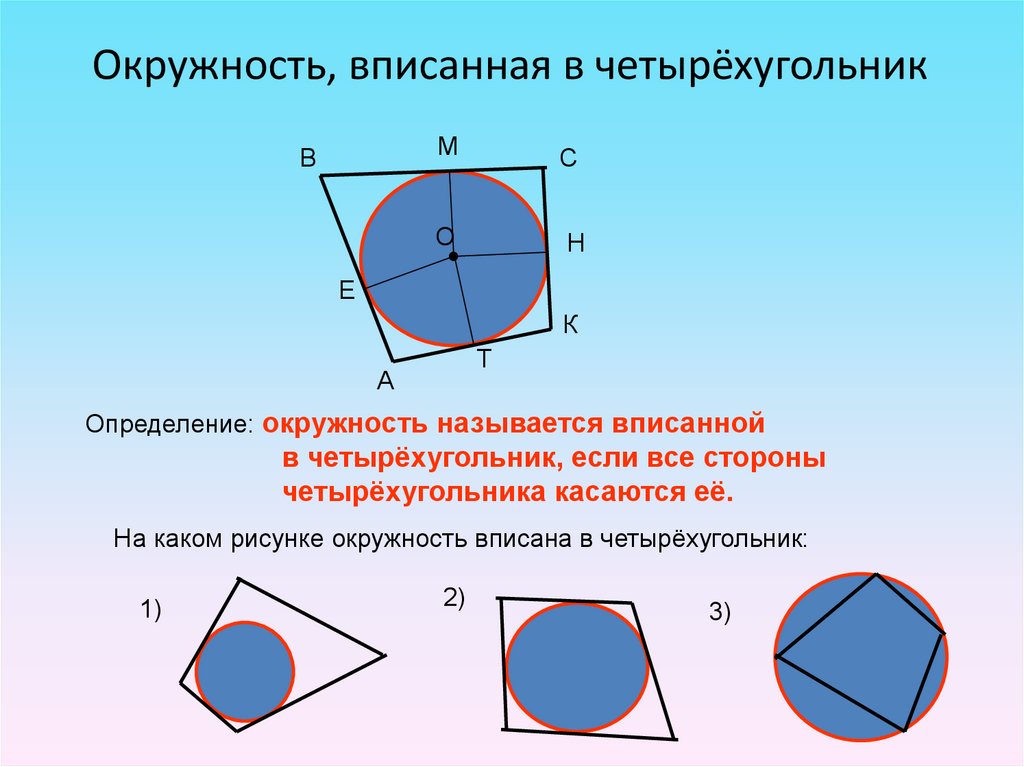
Центр окружности, вписанной в четырёхугольник — это точка пересечения биссектрис углов этого четырёхугольника. Радиус вписанной в квадрат окружности …
Еще по теме:
Еще по теме:
