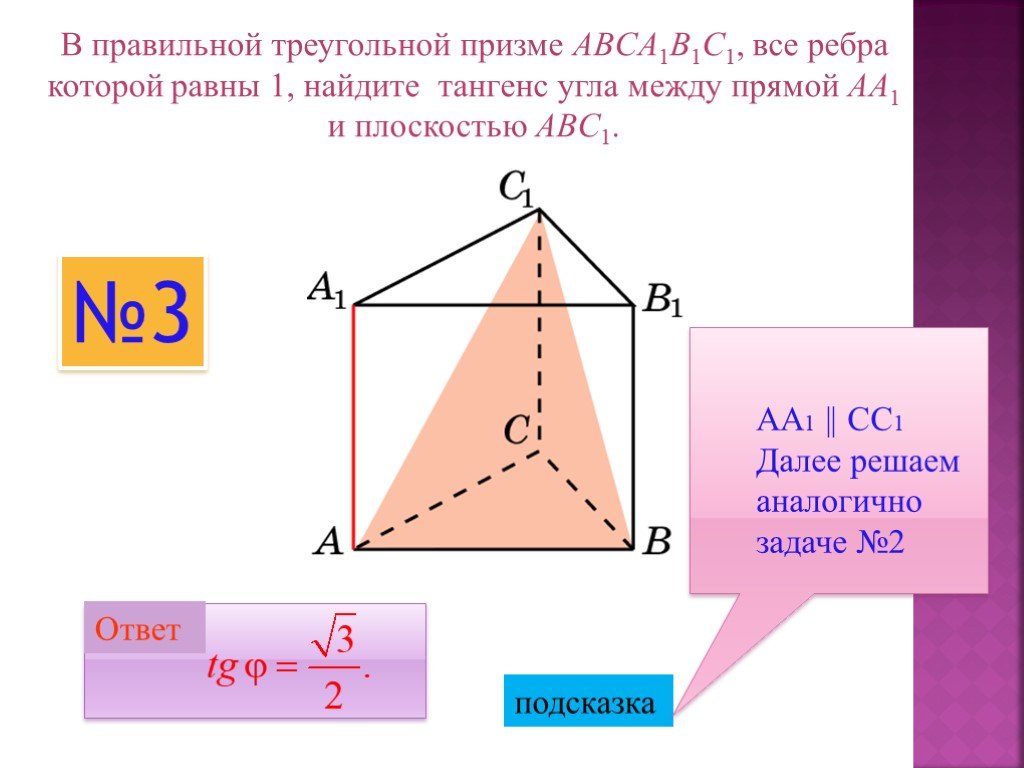
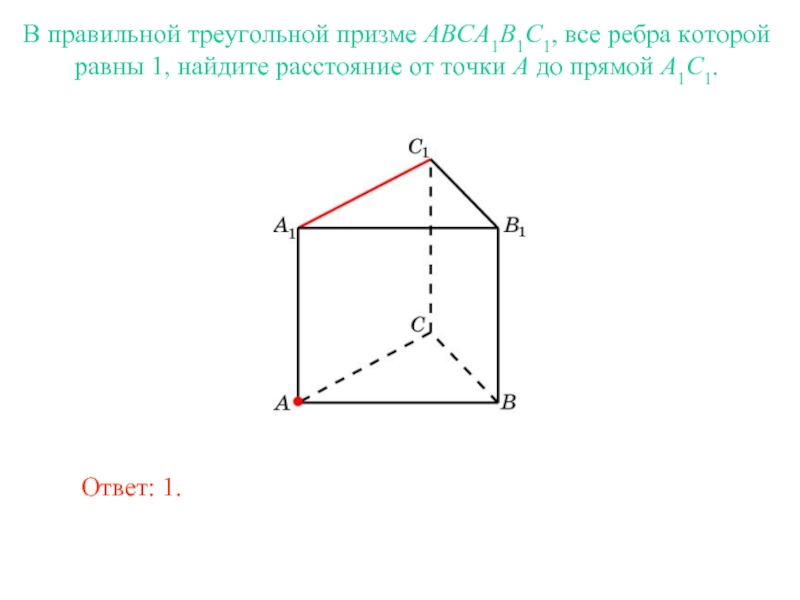
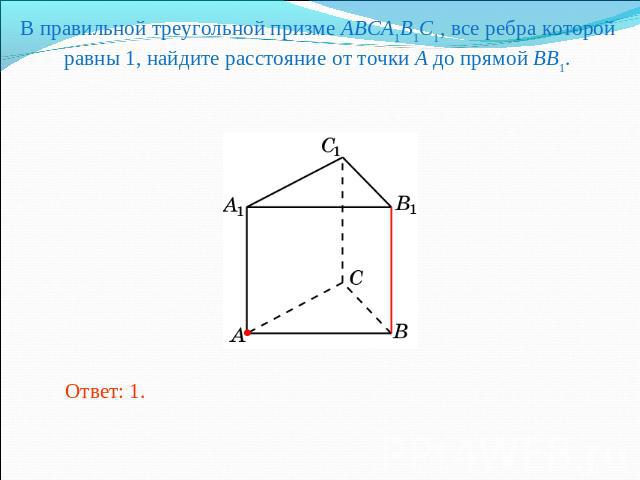
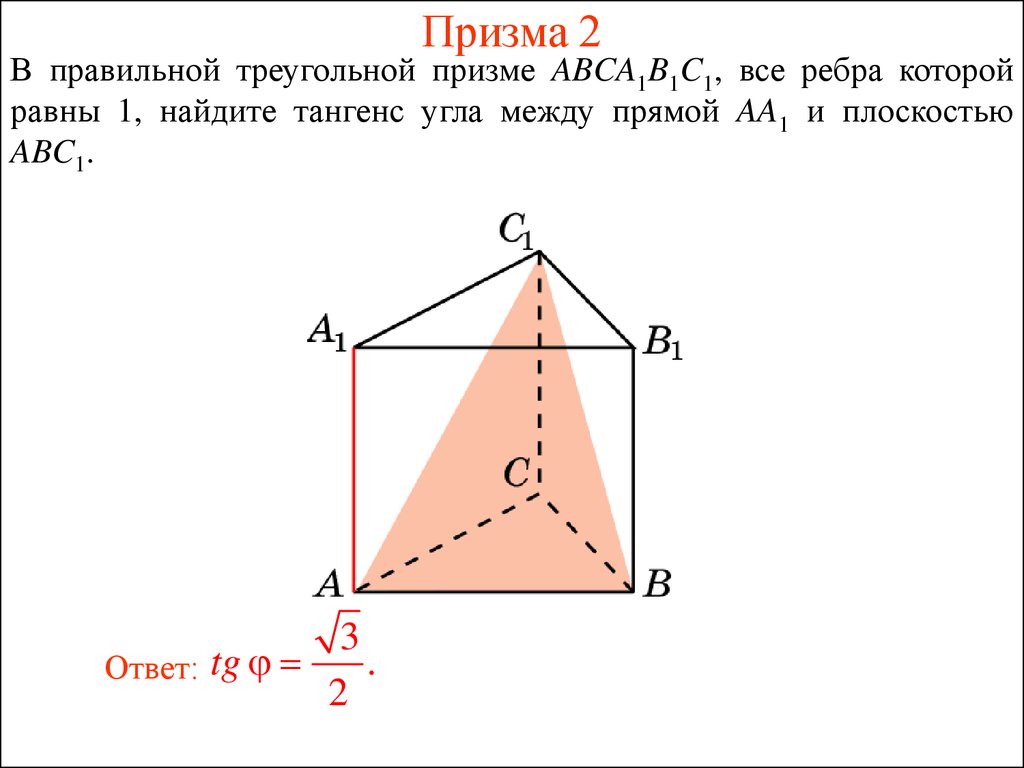
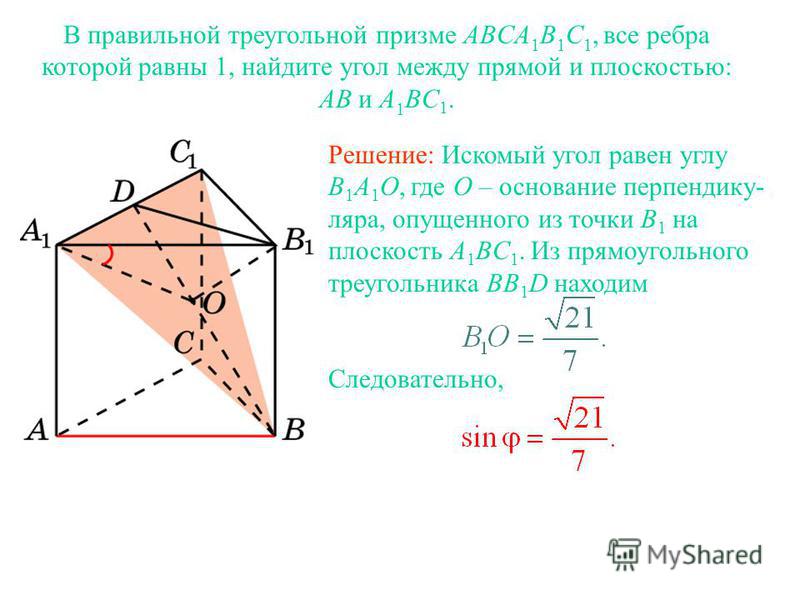
В правильной треугольной призме ABCA1B1C1 все рёбра равны 2. Точка M — середина ребра AA1. а) Докажите, что прямые MB и B1C перпендикулярны. б) Найдите расстояние …
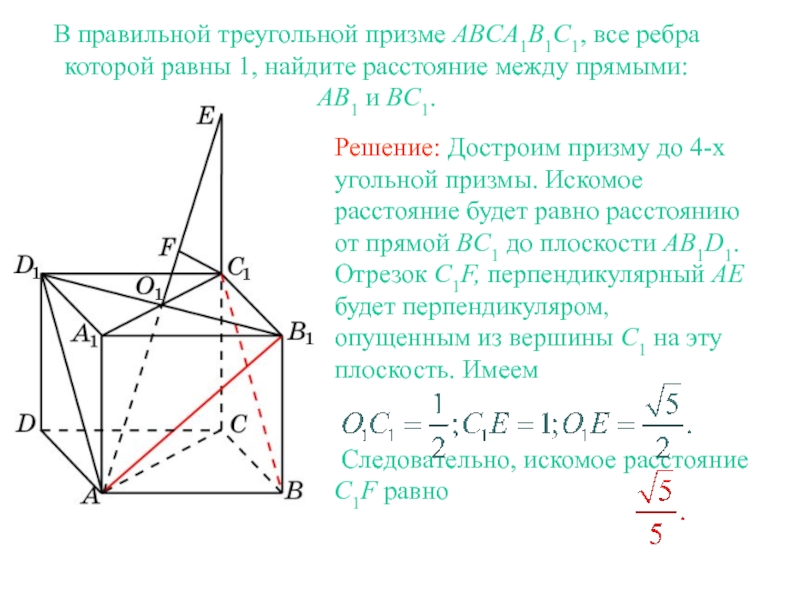Так как все ребра в призме равны, то ACC1A1 – квадрат со стороной 2. Проекция ребра BB1 на плоскость квадрата ACC1A1 показана синей линией на рисунке ниже. Из рисунка …
В правильной треугольной призме ABCA1B1C1 известны рёбра: ABAA1 = 4. Точка M — середина ребра BC. а) Докажите, что прямые B1C и C1M перпендикулярны. б) Найдите …
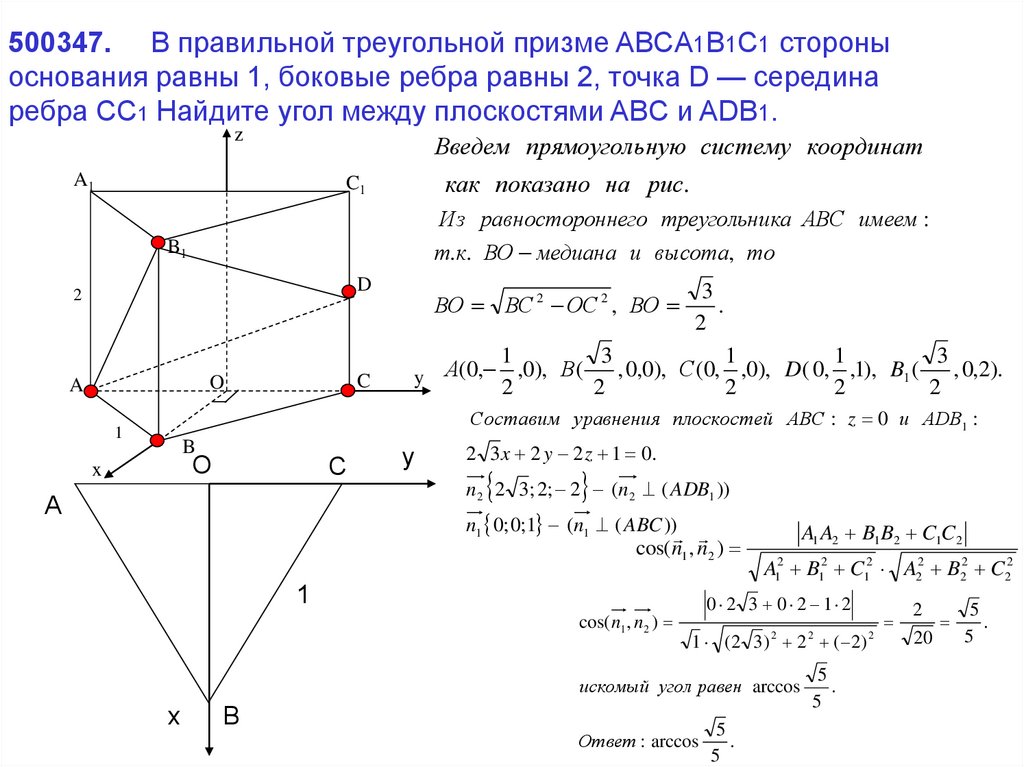
В правильной треугольной призме abca1b1c1 стороны основания равны 3, боковые ребра равны 1, точка d – середина ребра cc1. а) Постройте прямую пересечения плоскостей abc и adb1.
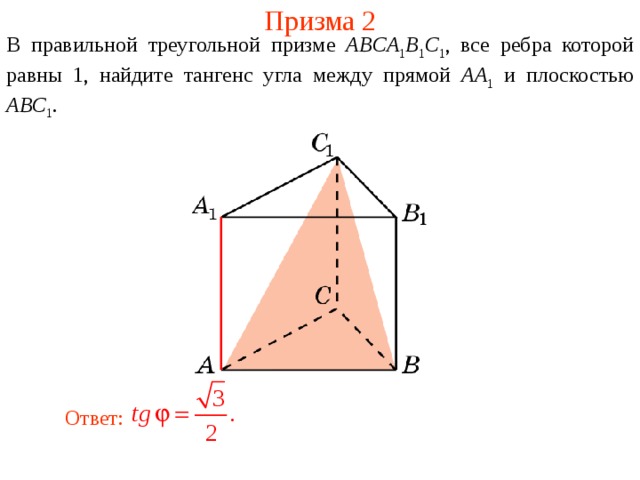
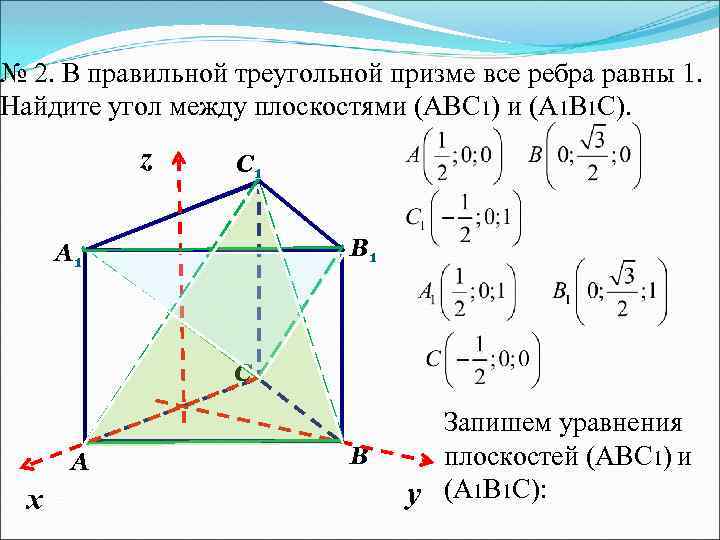
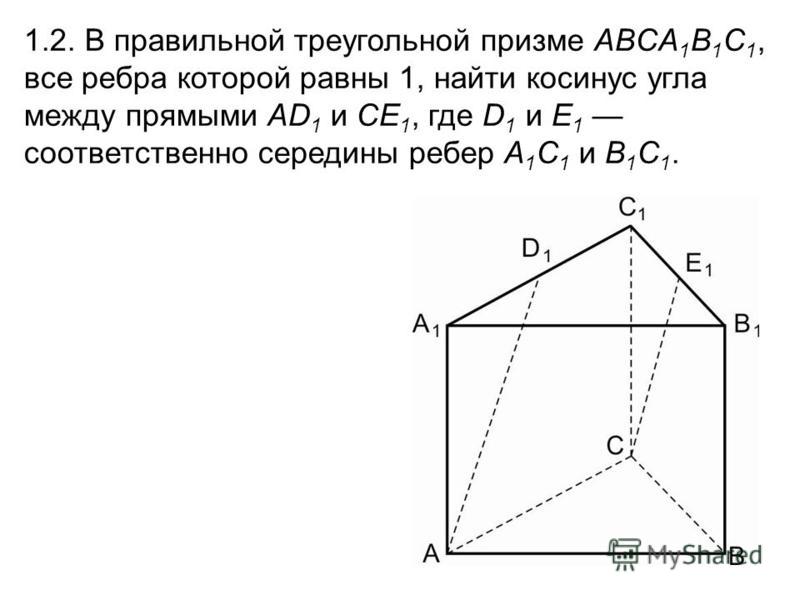В правильной треугольной призме abca1b1c1 все рёбра которой равны 2, найдите угол между прямыми bb1 и ac1. Ответ дайте в градусах.
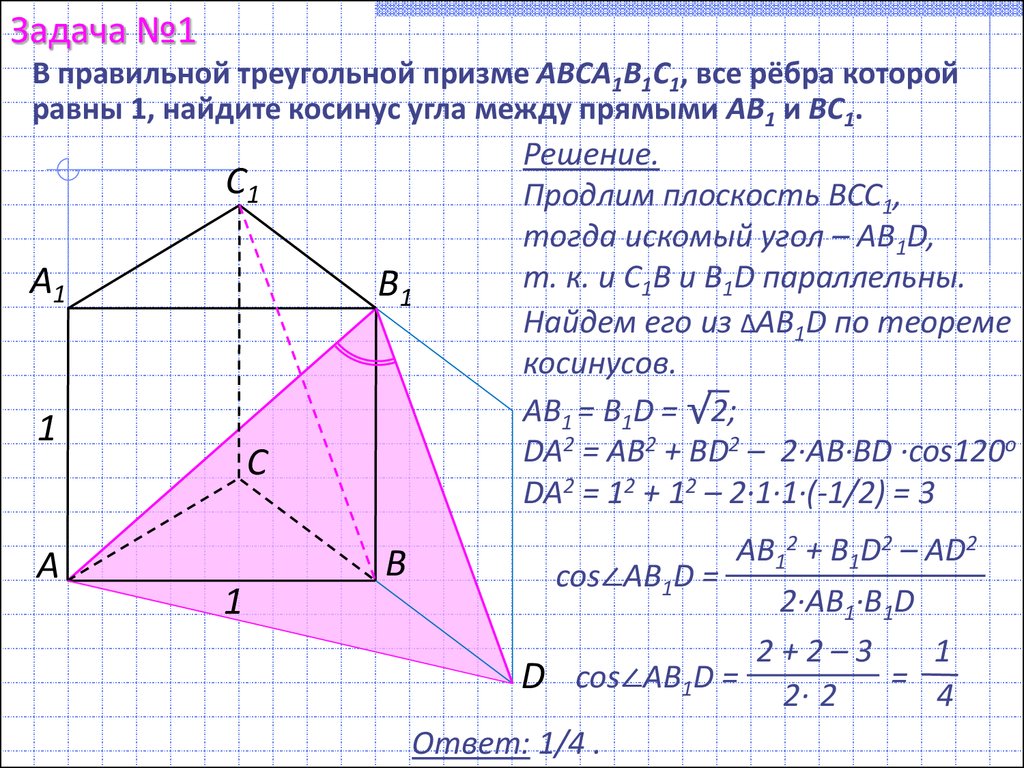
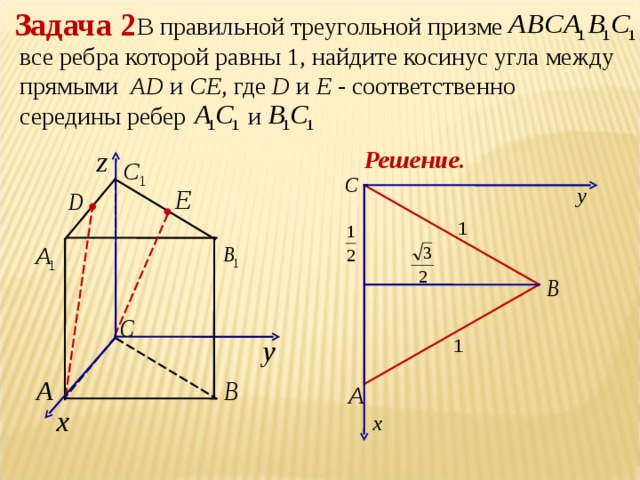
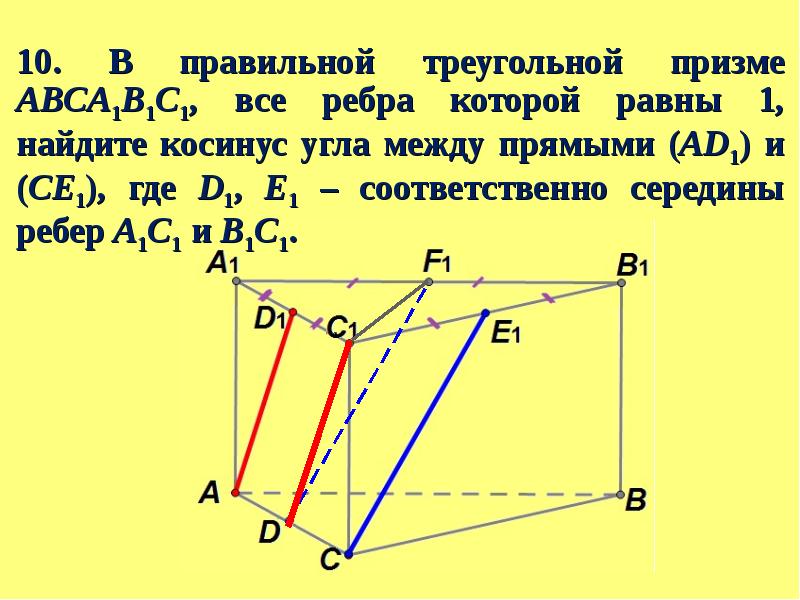
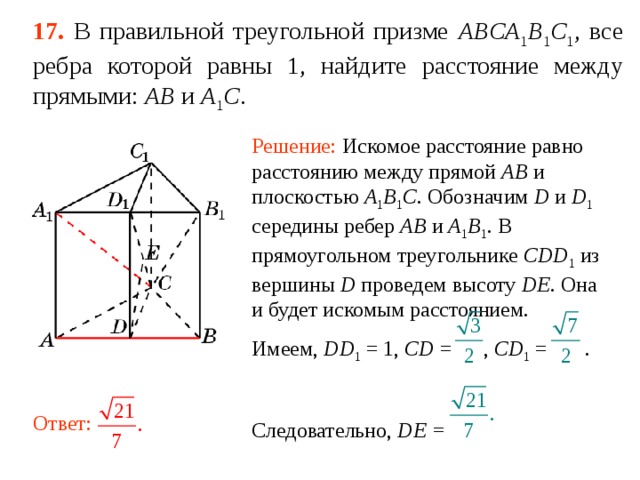
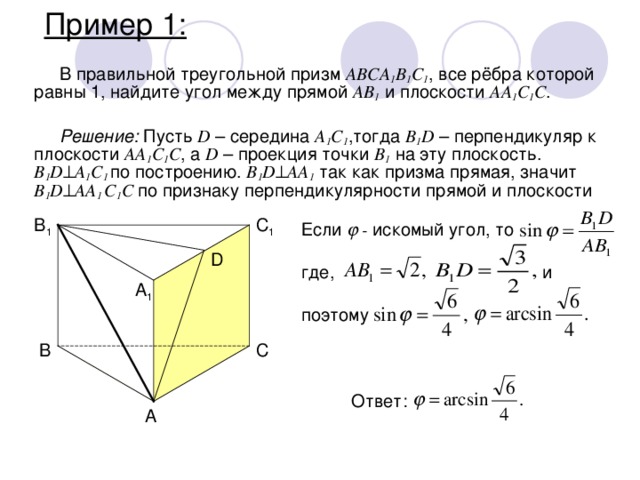
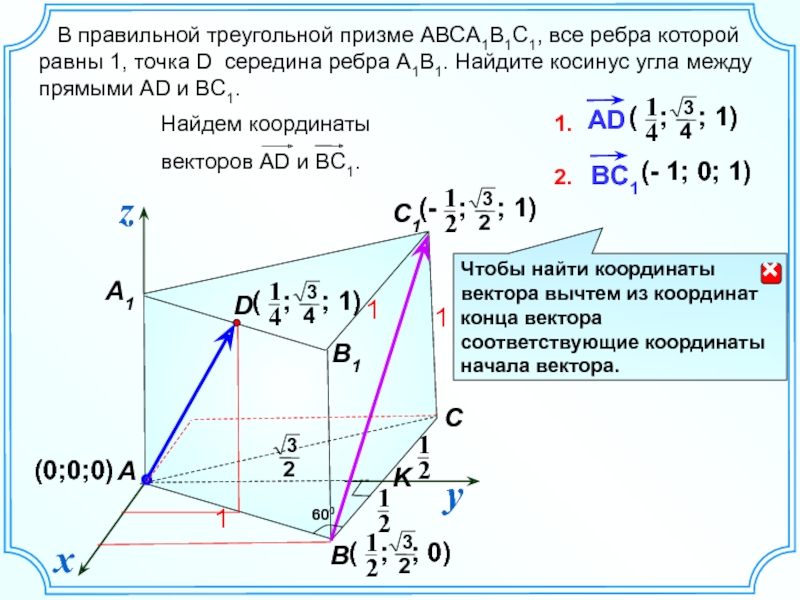
В правильной треугольной призме abca1b1c1, все ребра которой равны 1, найдите косинус угла между прямыми ab1 и bc1. математика 10-11 класс 27927
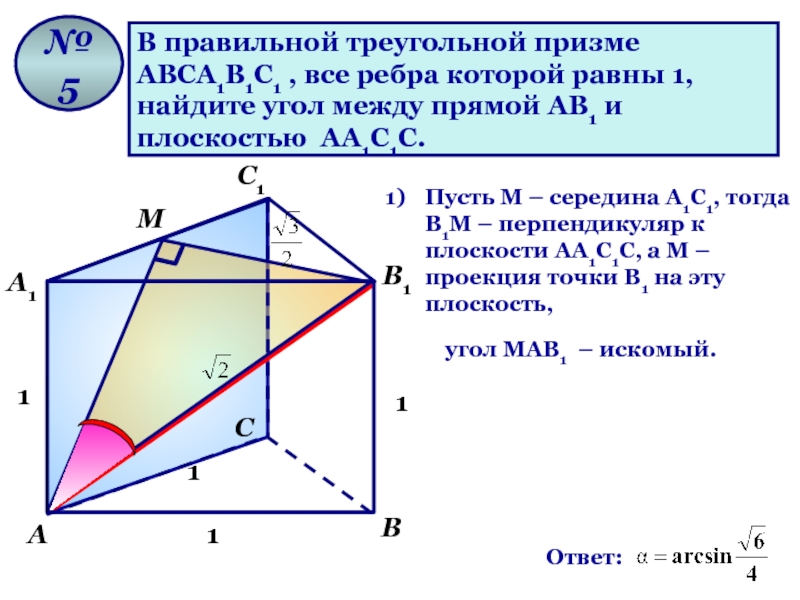
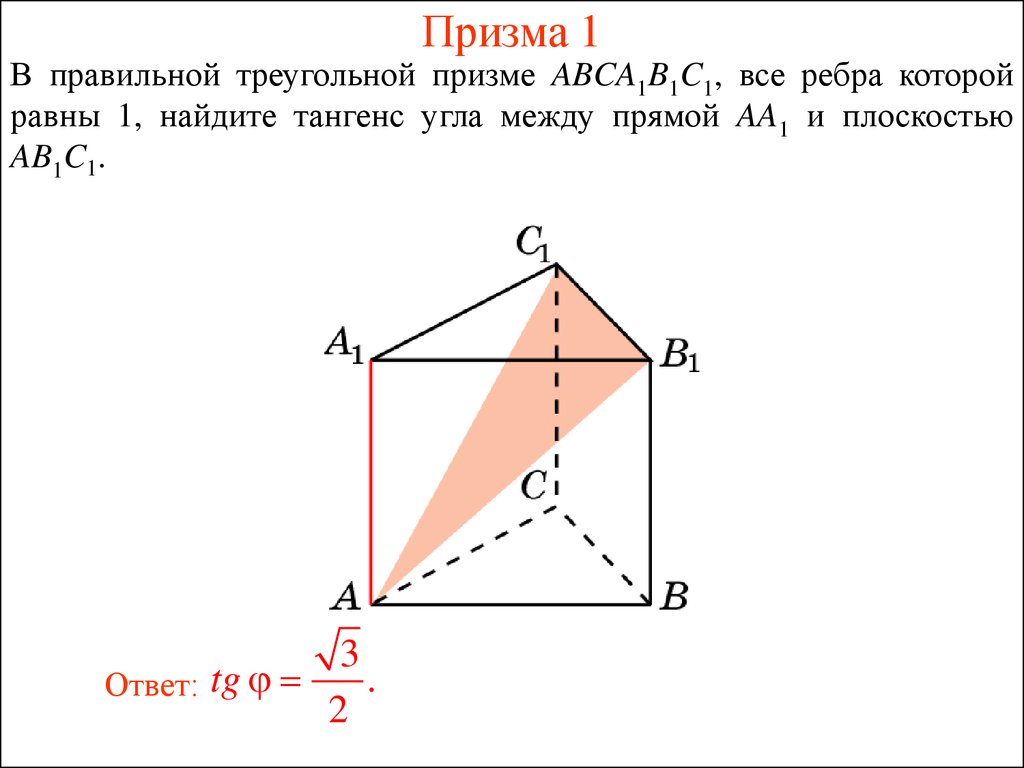В правильной треугольной призме ABCA1B1C1 все рёбра равны 1. а) Докажите, что прямая AB1 параллельна прямой, проходящей через середины отрезков AC и BC1. б) Найдите …
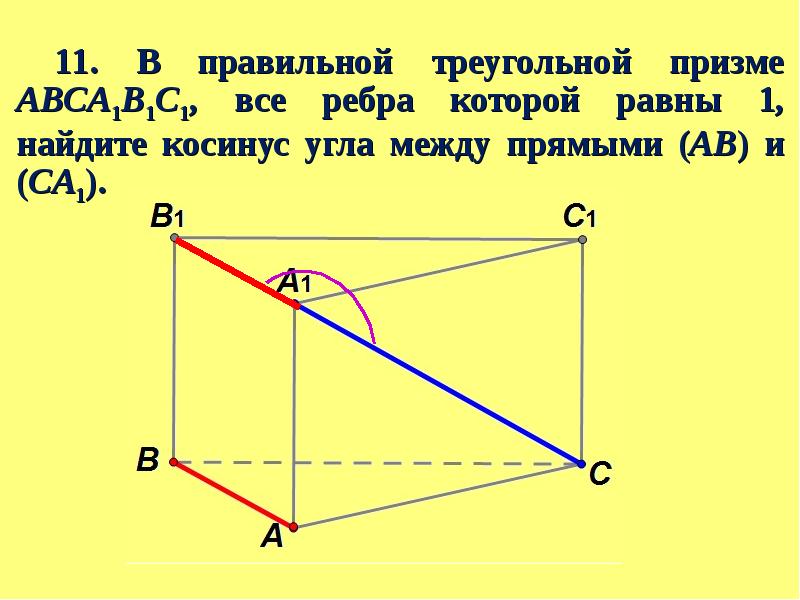
В правильной треугольной призме abca1b1c1, все ребра которой равны b, найдите: 1) угол между прямыми ab1 и bc; 2) расстояние между серединами отрезков ab и a1c
В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины …
В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 6, а боковое ребро AA1 равно 2 2–√. На рёбрах AB, A1B1 и B1C1 отмечены точки M, N и K …
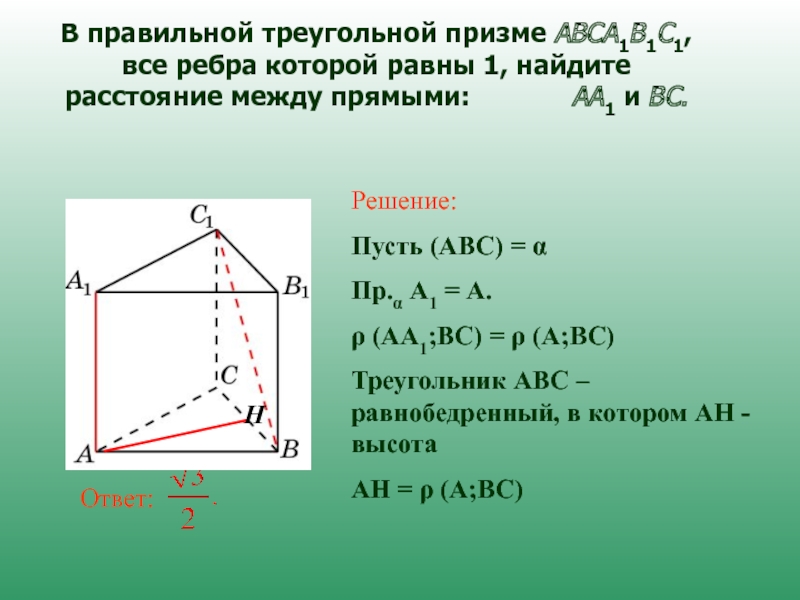В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 12, а высота призмы равна 2. На рёбрах B1C1 и AB отмечены точки P и Q соответственно, причём …
В правильной треугольной призме abca1b1c1 все рёбра равны 1. Точка e –середина ребра ac. а) Постройте сечение призмы плоскостью a1b1e; б) Найдите площадь этого сечения
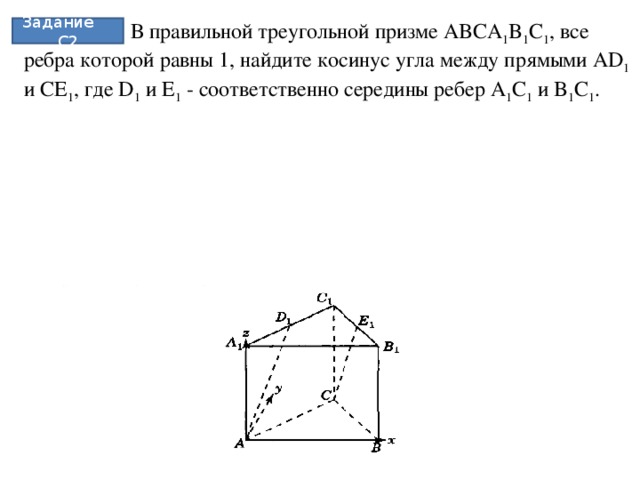В правильной треугольной призме все рёбра равны . Через точки и середину ребра проведена плоскость. Докажите, что сечение призмы указанной плоскостью является …
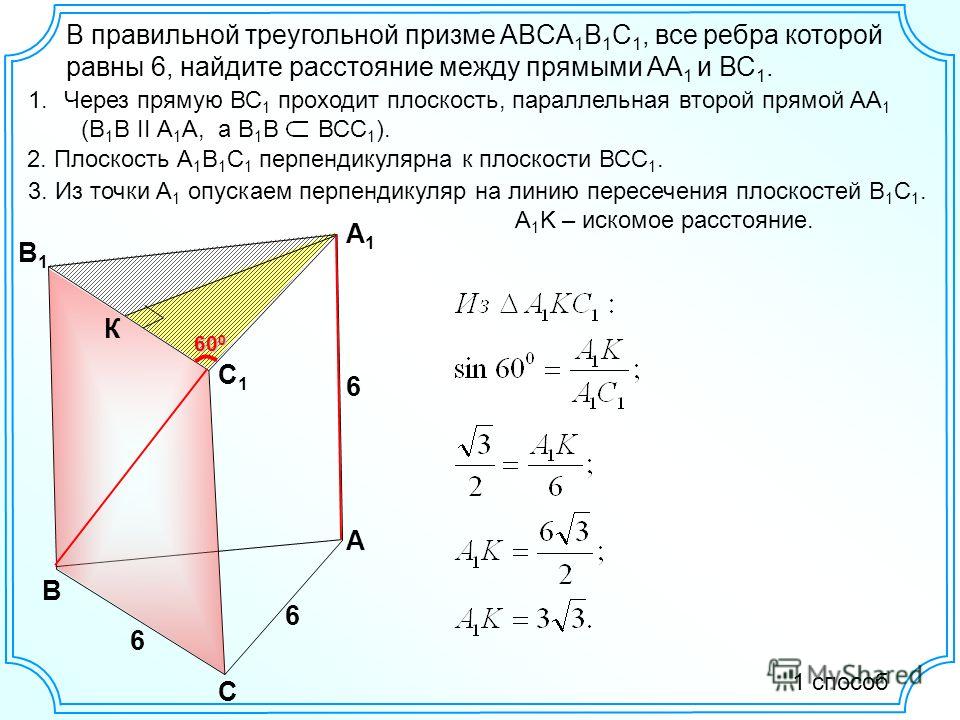
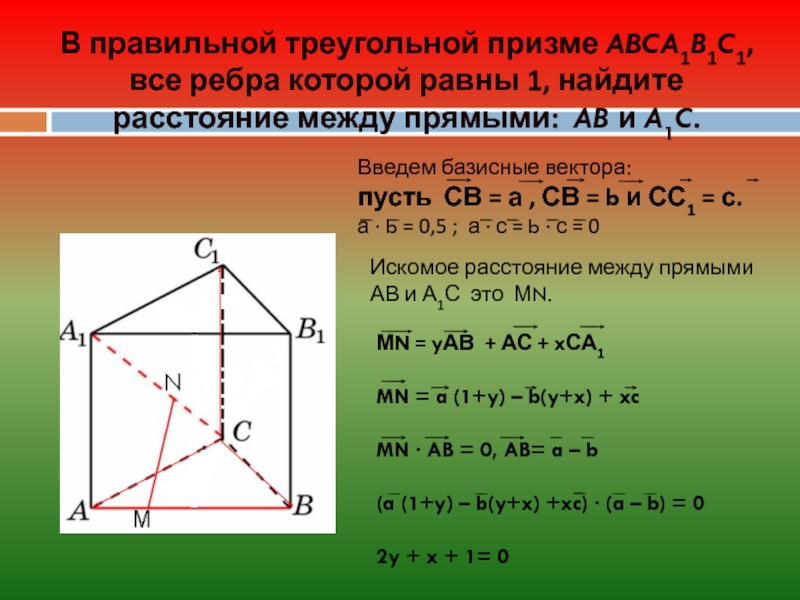В прямоугольном треугольнике АСН, по теореме Пифагора, СН 2 = АС 2 – АН 2 = 1 – 1 / 4 = 3/4. СН = √3 / 2 см. Построим сечении А1СВ1 и проведем в нем высоту СК. Угол КСН …
В правильной треугольной призме ABCA1B1C1 стороны основания равны 4, боковые рёбра равны 7, точка D — середина ребра BB1. а) Пусть прямые C1D и BC пересекаются в …
Пифагора: AC₁=√2;BC₁=√2. Ответ есть, нужен ход решения.
Еще по теме:
Еще по теме:
