Теорема о биссектрисе часто применяется для решения задач, связанных с треугольниками. Звучит она следующим образом: Биссектриса, опущенная из вершины …
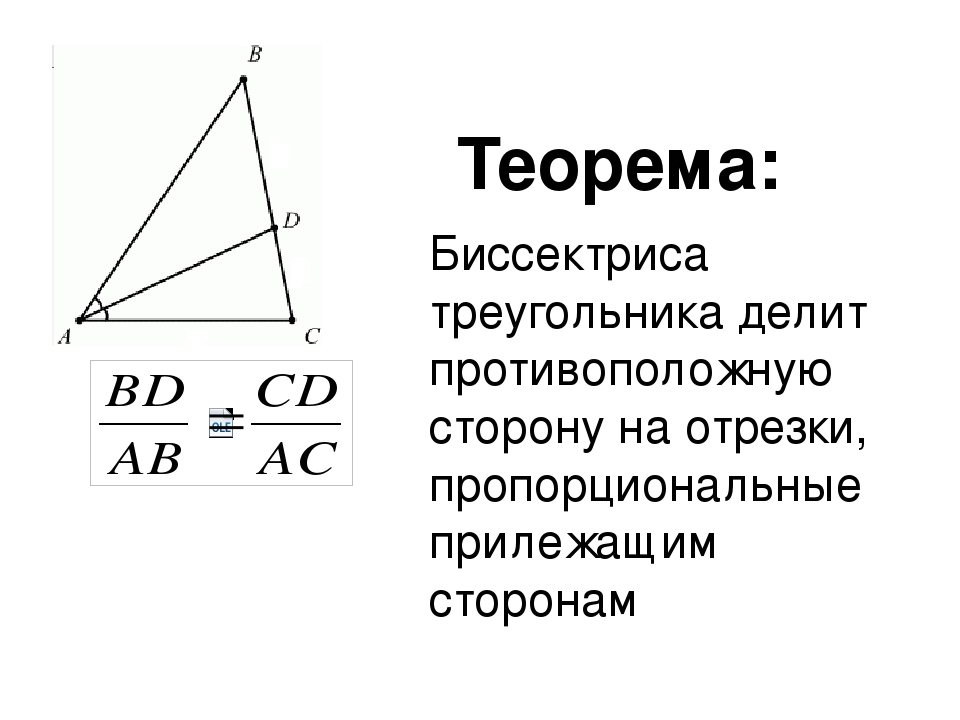
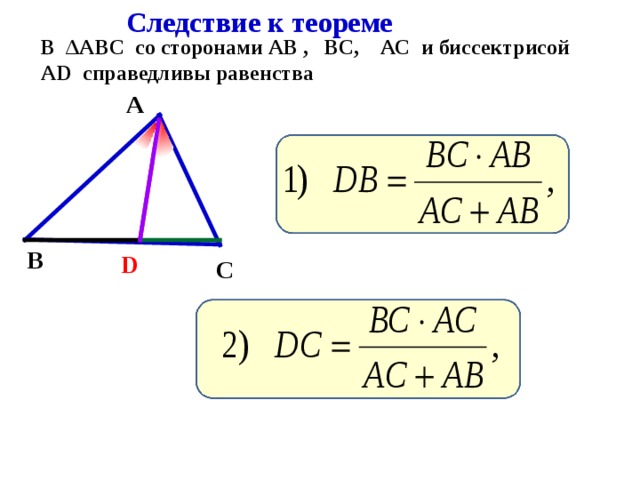
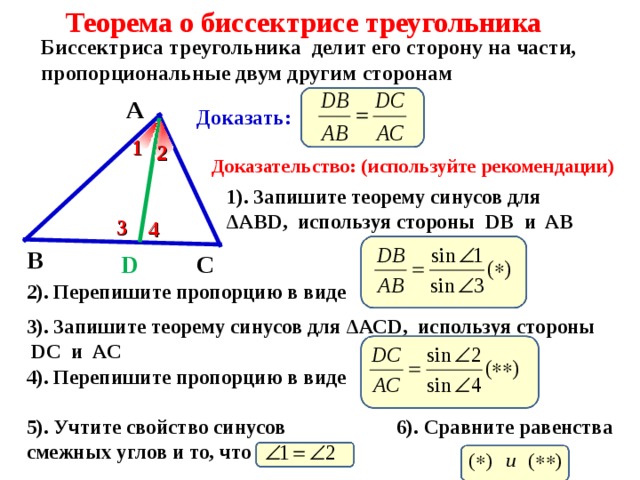
Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине.
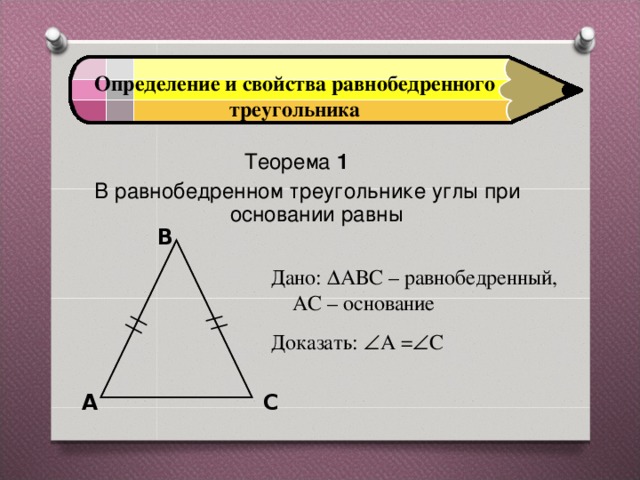
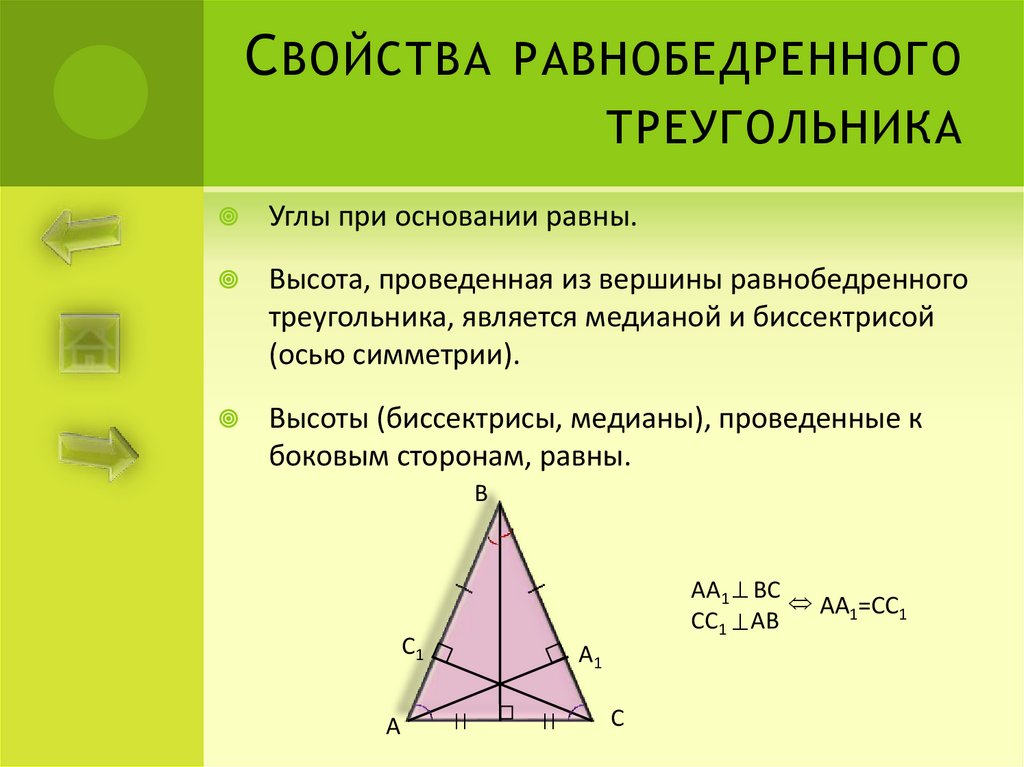
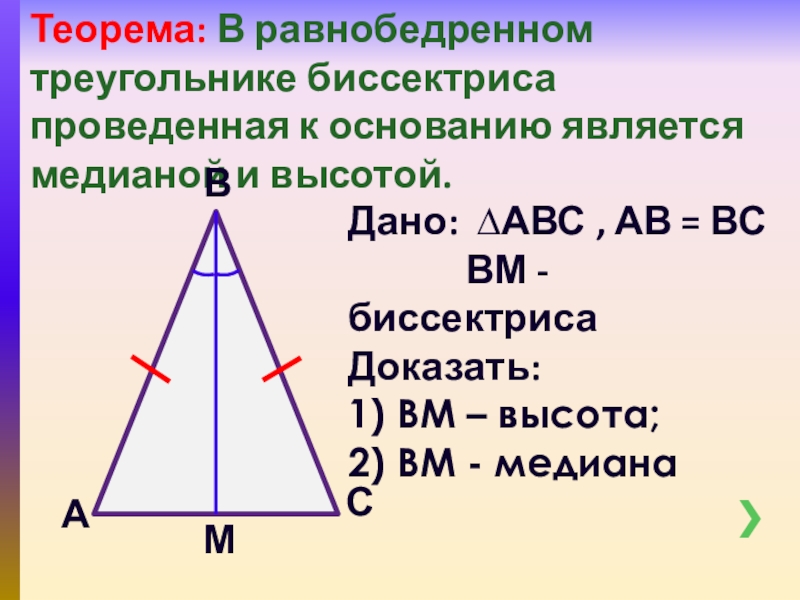
Свойства биссектрис равнобедренного треугольника. i. Биссектрисы углов при основании равнобедренного треугольника (проведенные к боковым сторонам), равны. Дано: ∆ abc, …
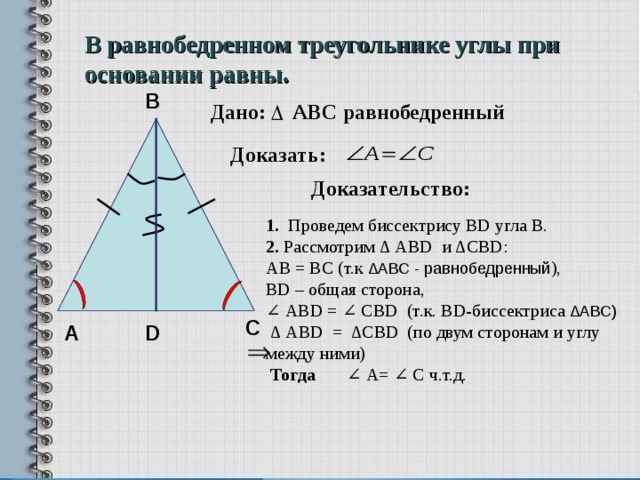
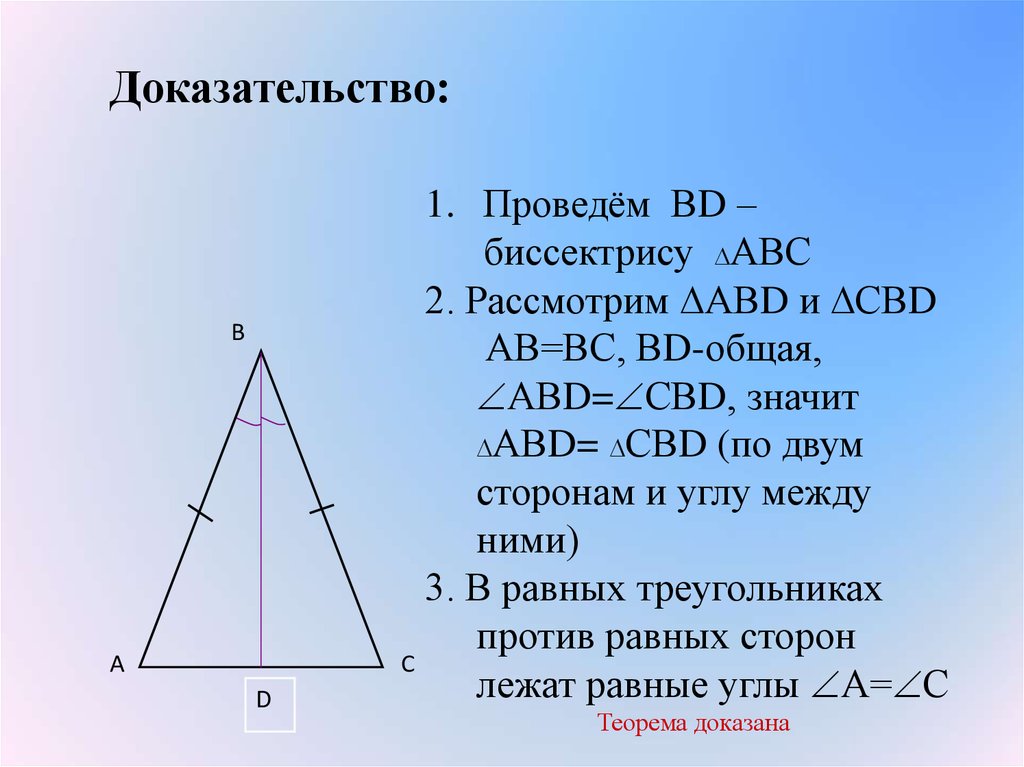
Рассмотрим треугольники АКВ и СКВ: АВ=ВС – по условию треугольник АВС – равнобедренный; ∠АВК = ∠КВС, так как ВК – биссектриса; ВК – общая сторона.
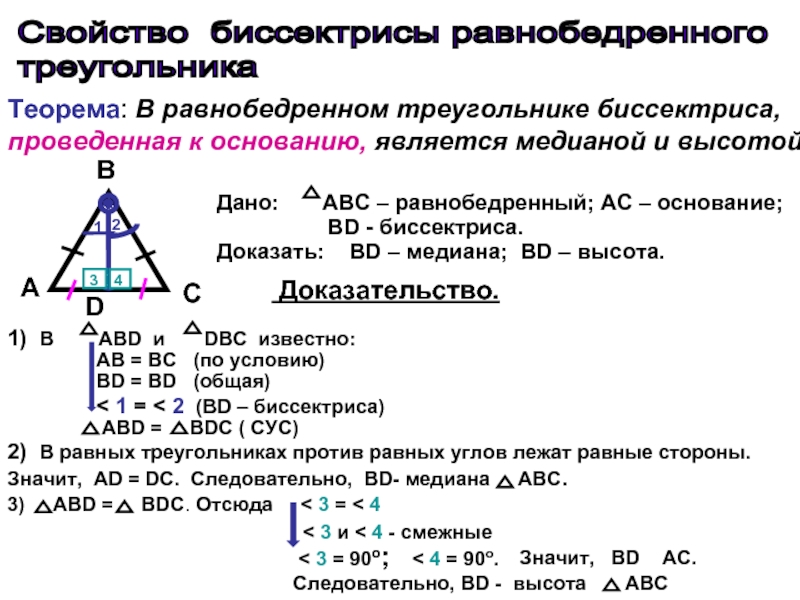
Биссектриса совпадает с медианой и высотой, а, значит, станет катетом малого прямоугольного треугольника, тогда значение биссектрисы можно найти как значение катета через теорему Пифагора.
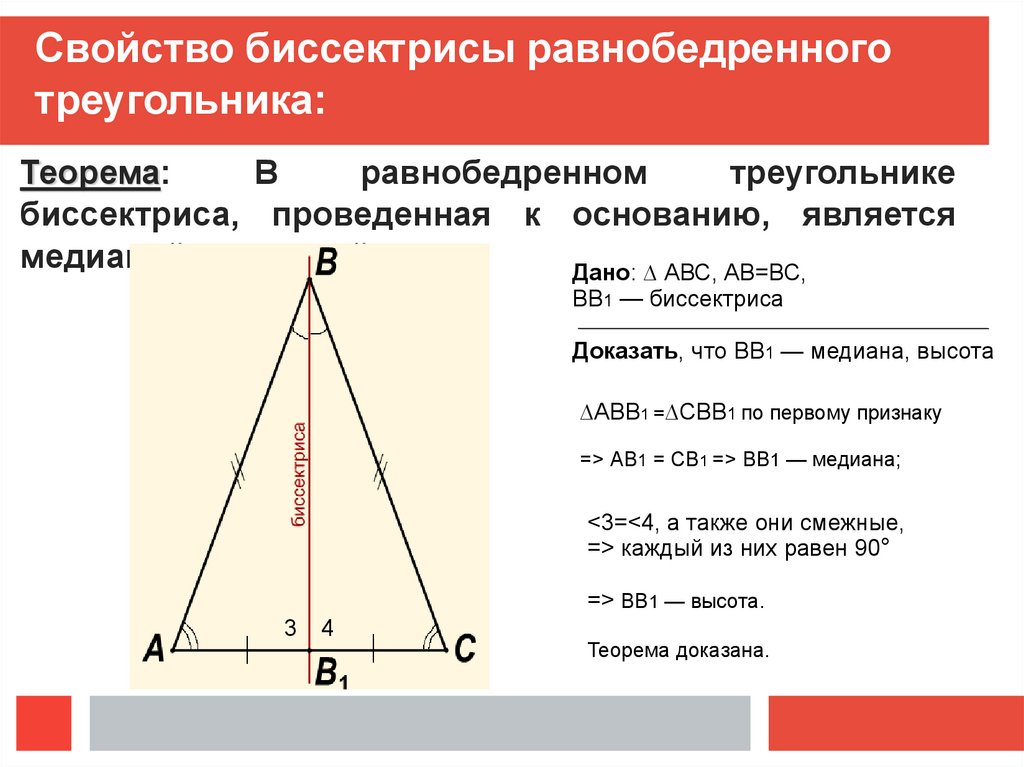
Биссектриса треугольника — это отрезок, который является частью биссектрисы угла треугольника и соединяет вершину треугольника с точкой на противоположной стороне.
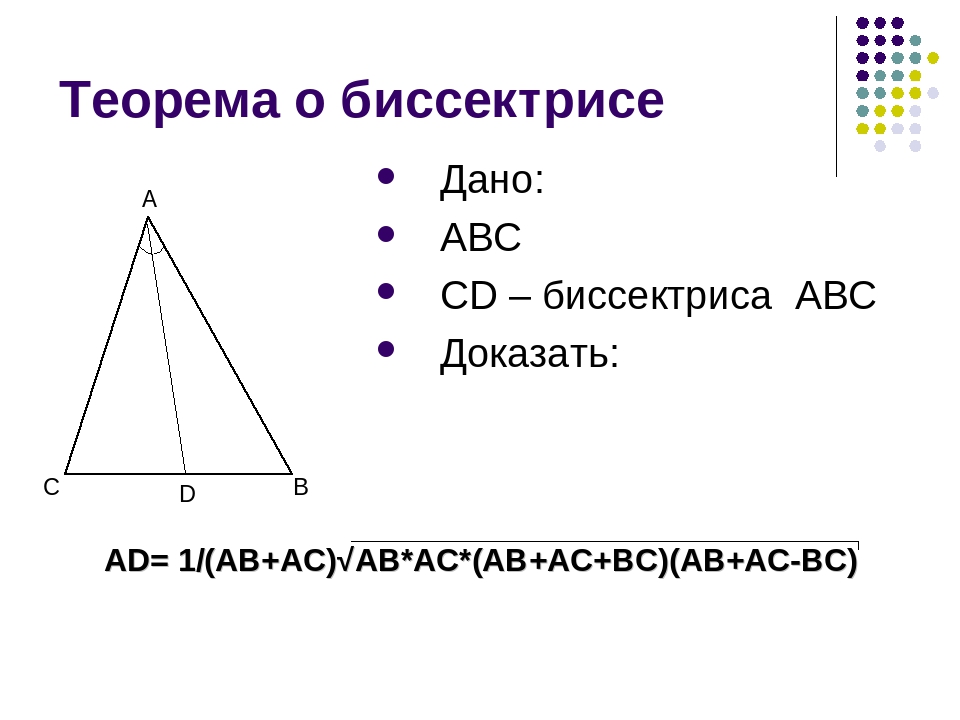
Треугольники - Теорема о биссектрисе: b, c - стороны треугольника , m, n - части, на которых биссектриса делит противоположную сторону a
Приводятся определения, формулы, теоремы и примеры решения задач на вычисление элементов равнобедренного треугольника с помощью его биссектрисы.
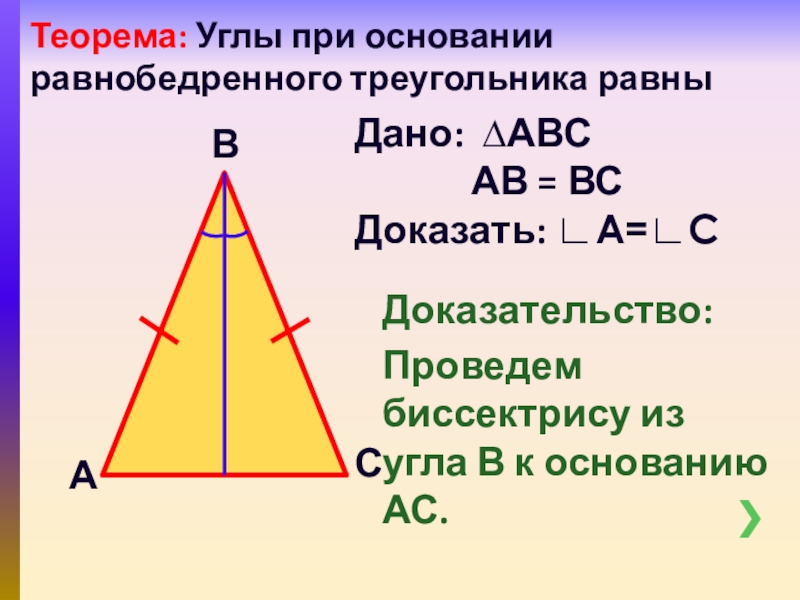Теорема о биссектрисе формулируется следующим образом: биссектриса треугольника делит его сторону, к которой она проведена, на отрезки, пропорциональные двум другим …
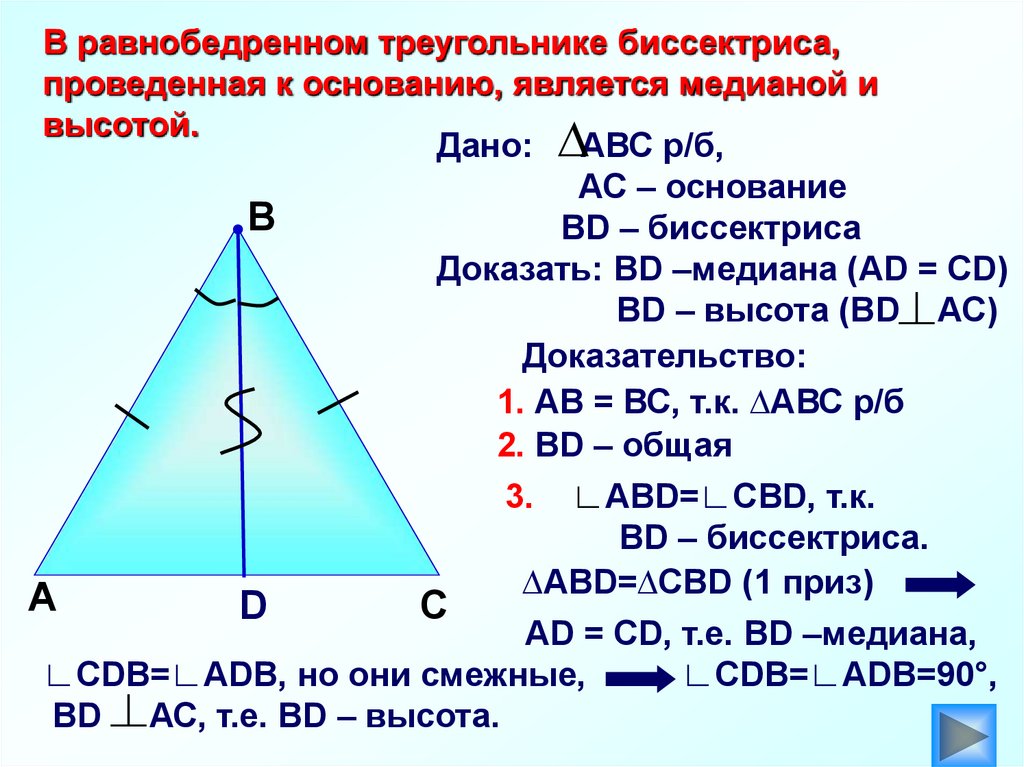
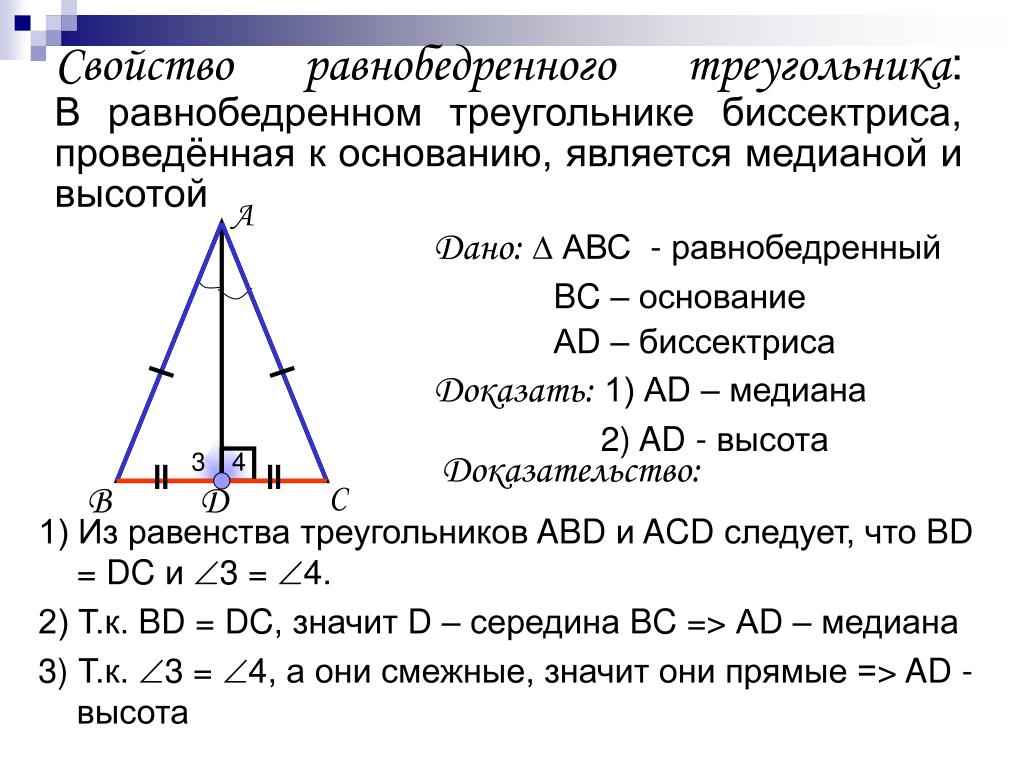
Рассмотрим равнобедренный треугольник АВС (АВ=ВС). СМ – биссектриса угла у основания. Докажем, что: Доказательство свойства биссектрисы угла при основании равнобедренного треугольника. Шаг 1. По свойству …
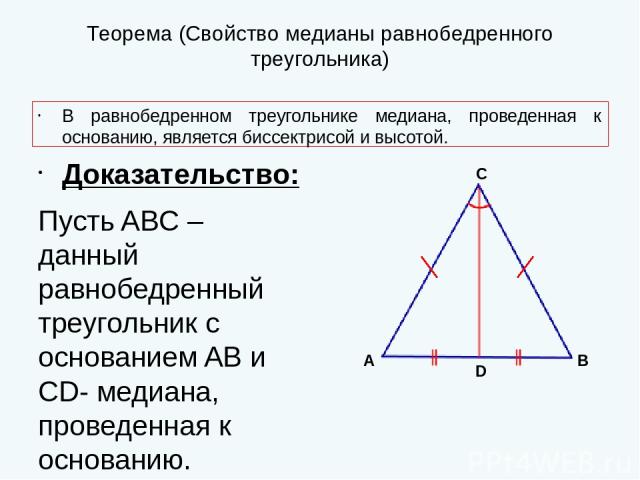
Рассмотрим свойство биссектрисы треугольника с доказательством и задачу на применение свойства. Теорема (Свойство биссектрисы треугольника) Биссектриса …
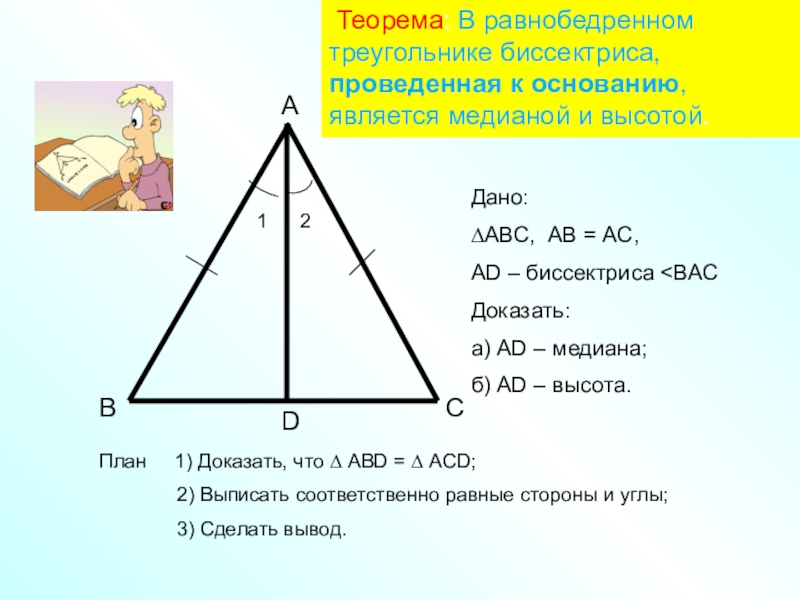Биссектриса при вершине треугольника делит противоположную сторону на два отрезка, пропорциональных сторонам треугольника, прилежащим к данным отрезкам.
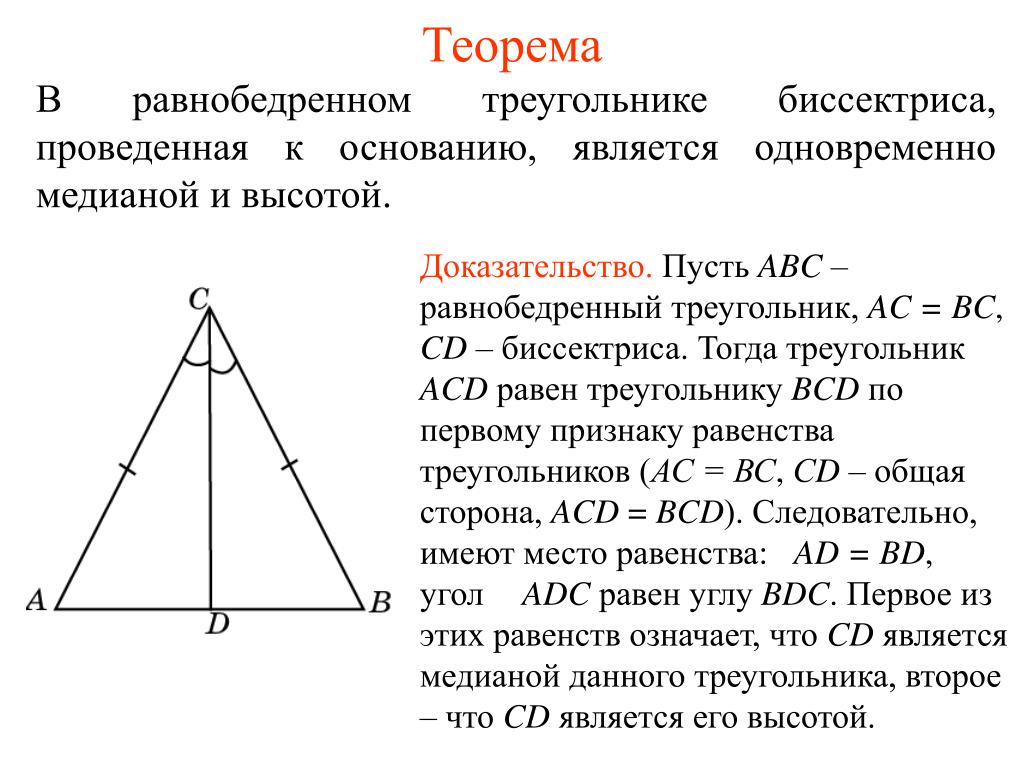
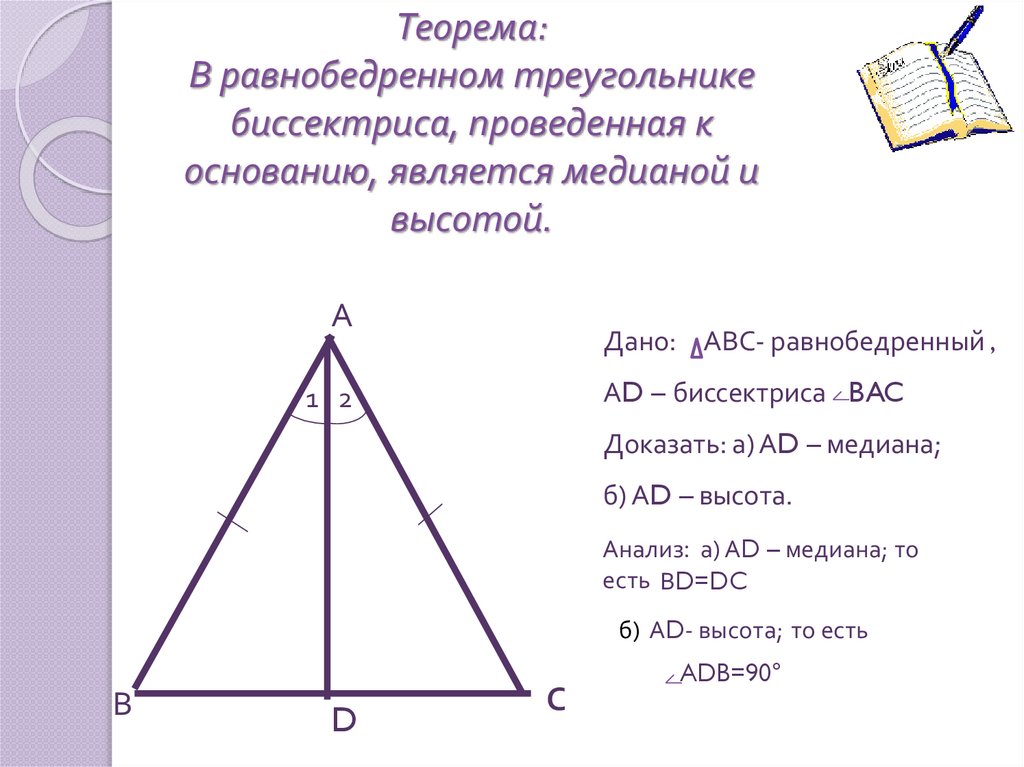Доказательство теоремы о биссектрисе основано на свойствах равнобедренного треугольника. Рассмотрим треугольник ABC, в котором BD - …
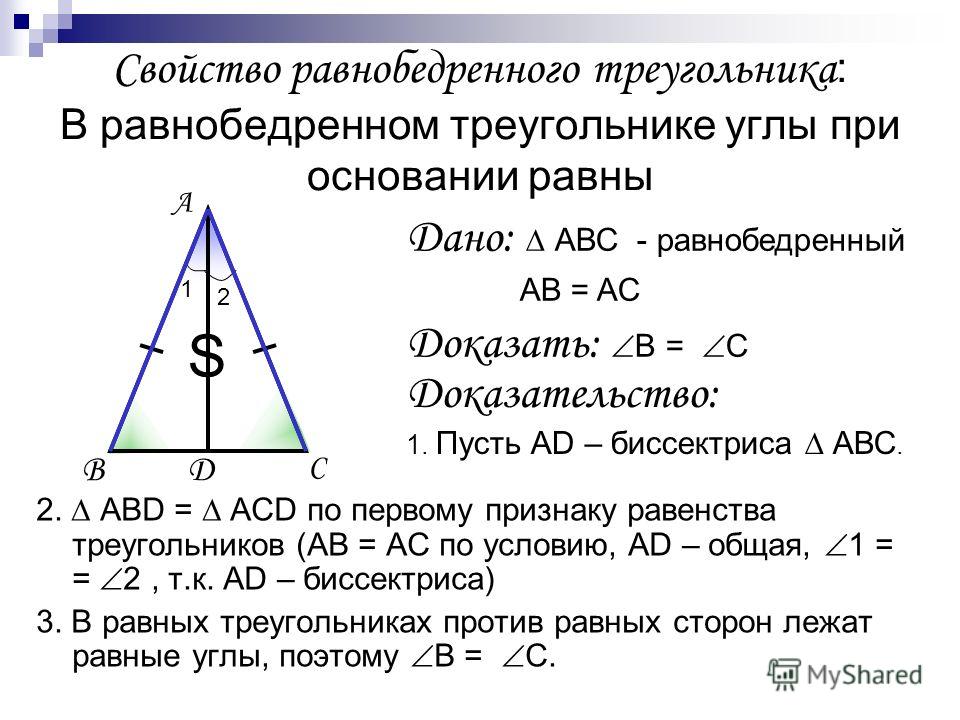
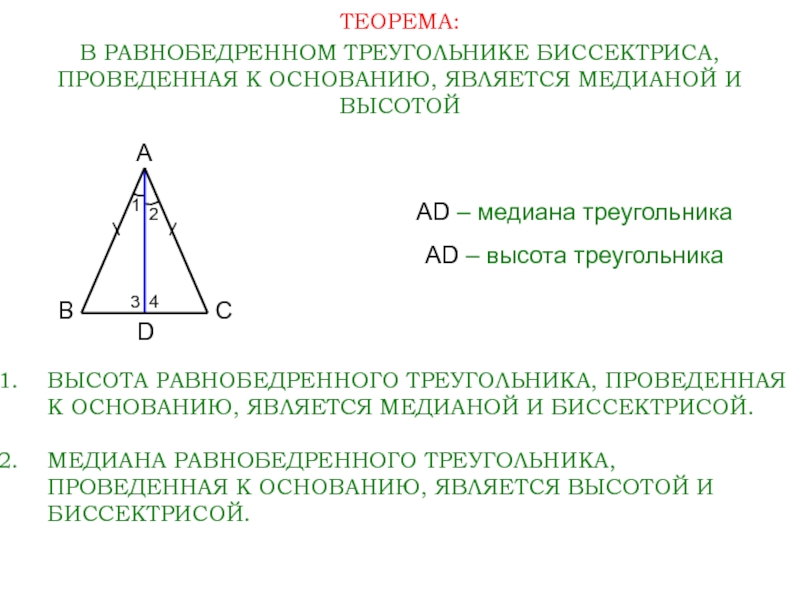
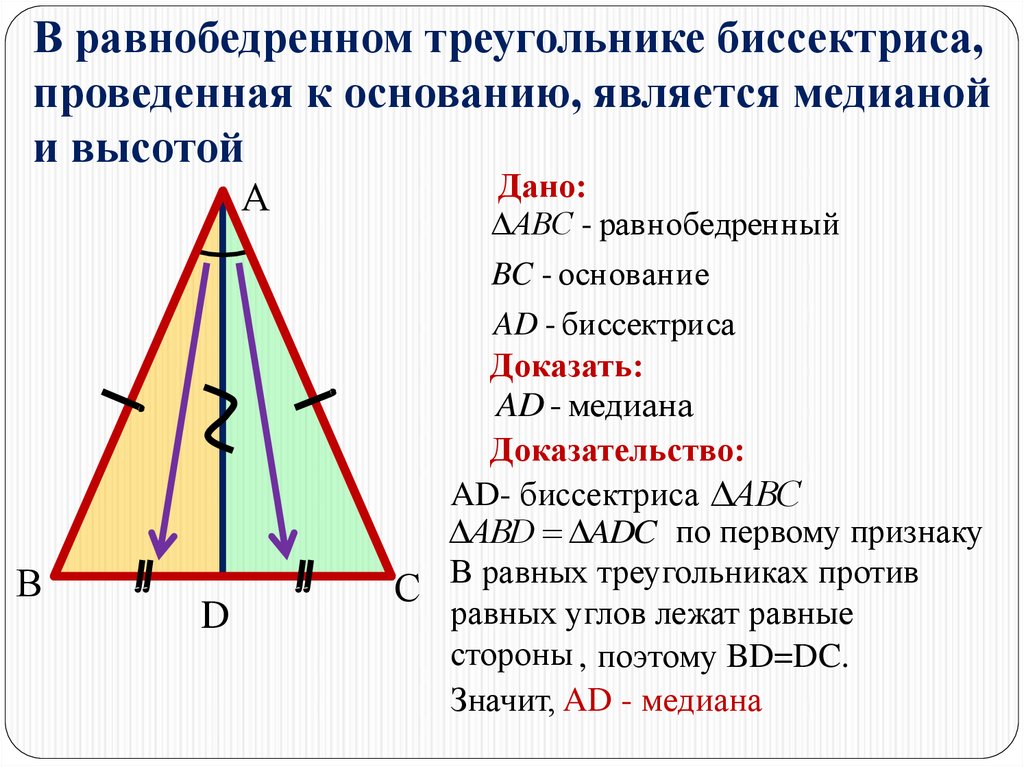
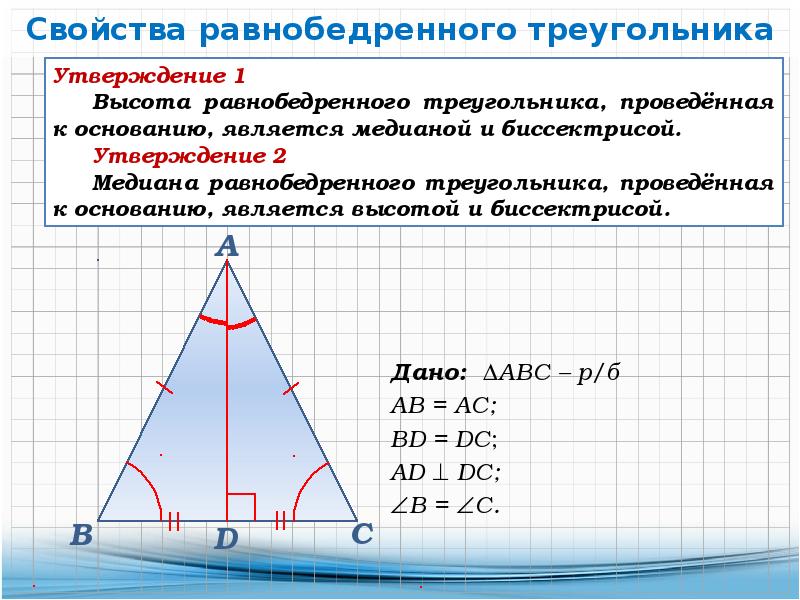
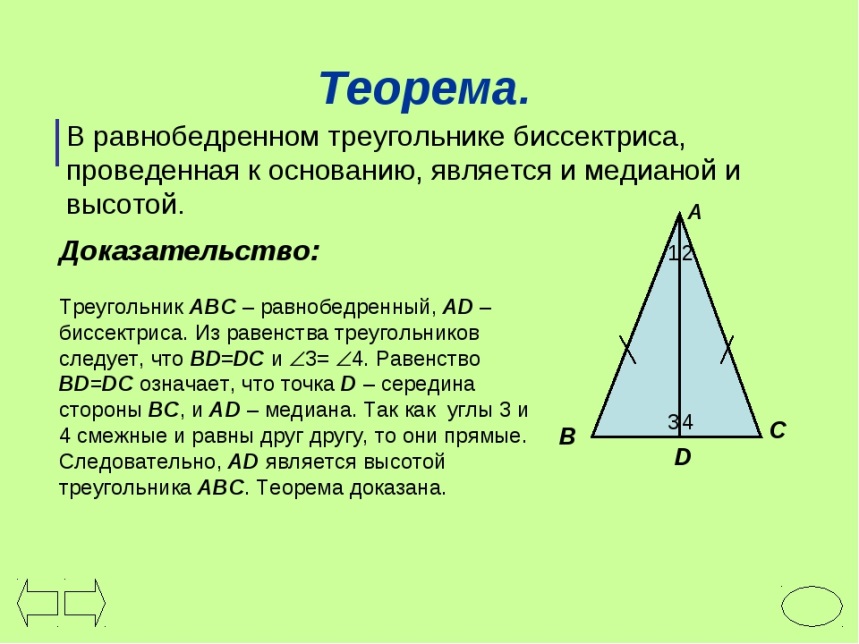
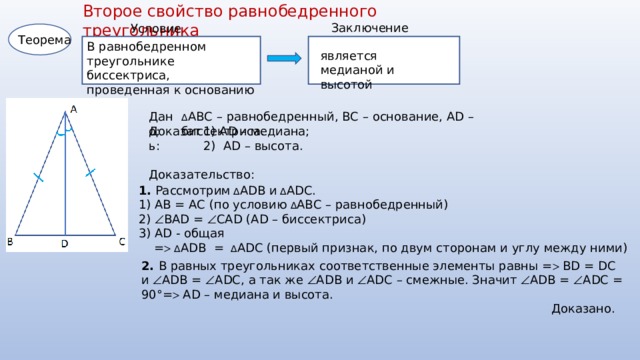
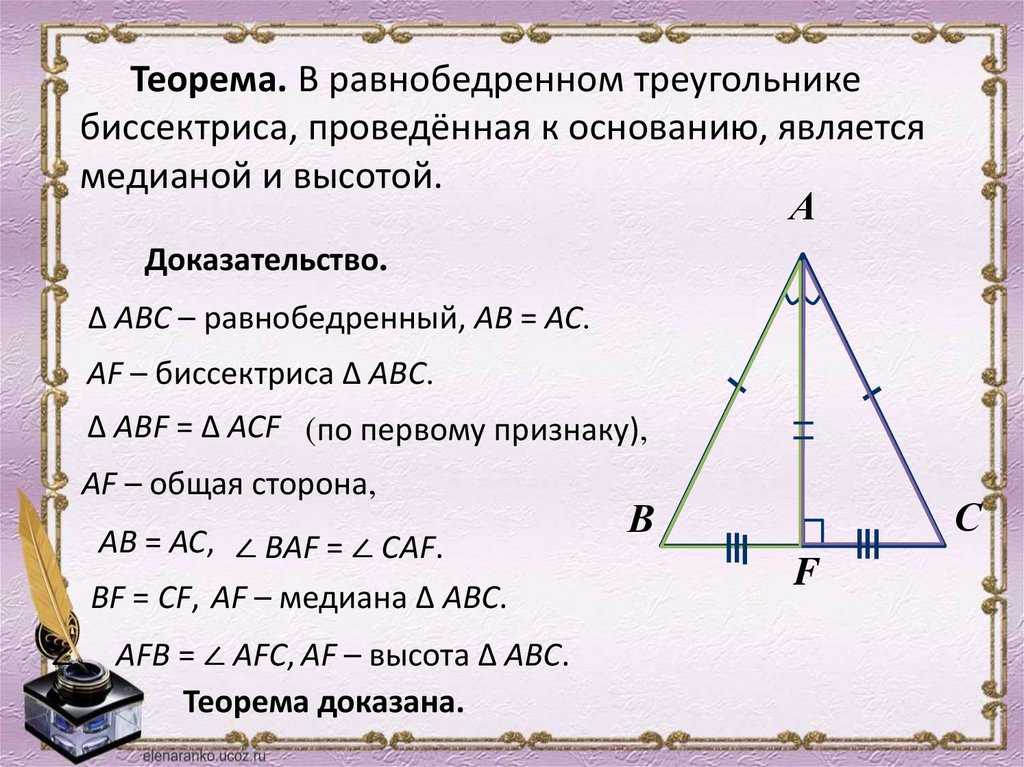
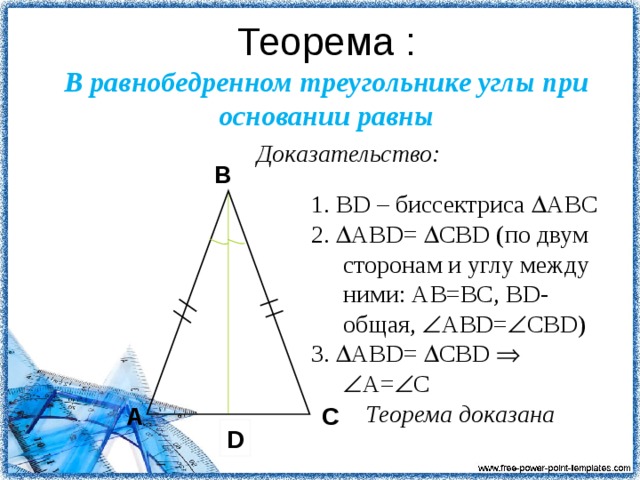Обратимся к рисунку, на котором АВС — равнобедренный треугольник с основанием ВС, АD — его биссектриса. Из равенства треугольников АВD и АСD (по 2 признаку равенства …
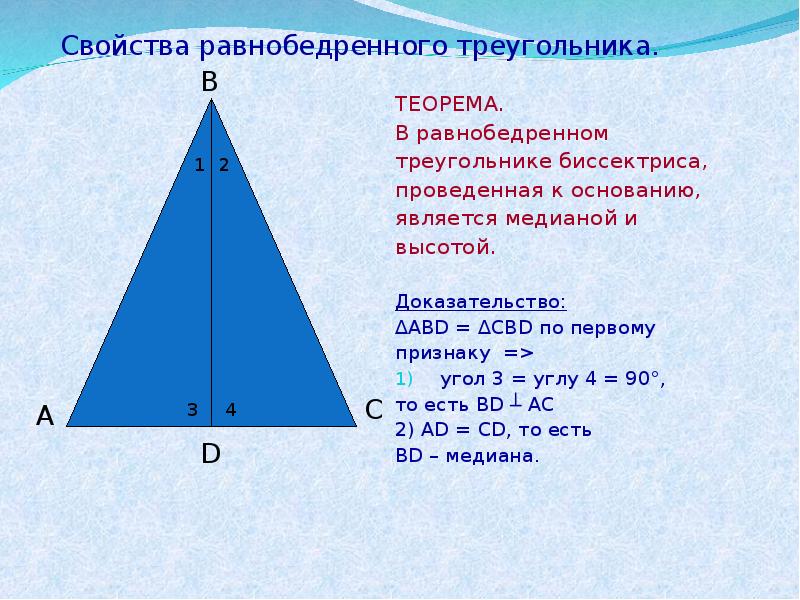Обратная формулировка: если две из трех биссектрис в треугольнике равны, значит он является равнобедренным. В равнобедренном треугольнике биссектриса, проведенная …
Еще по теме:
Еще по теме:
