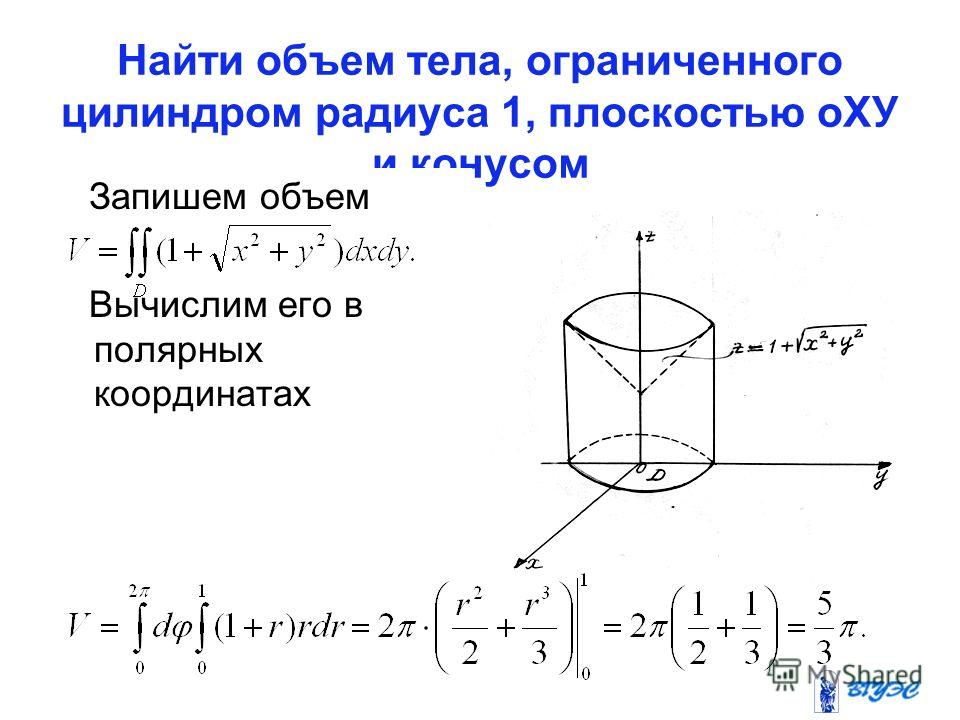
С помощью тройного интеграла найти объем тела, ограниченного поверхностями . Скромно и со вкусом. Решение: данное тело ограничено конической поверхностью и …
Данный калькулятор предназначен для расчета объема тела, ограниченного двумя поверхностями. Для расчета необходимо ввести уравнения этих поверхностей в …
Тело ограничено осью OZ и плоскостями x^2 + y^2 = 1 и x^2 + y^2 = z^2. Поскольку z ≥ 0, мы рассматриваем только верхнюю половину тела. Объем тела можно найти с помощью …
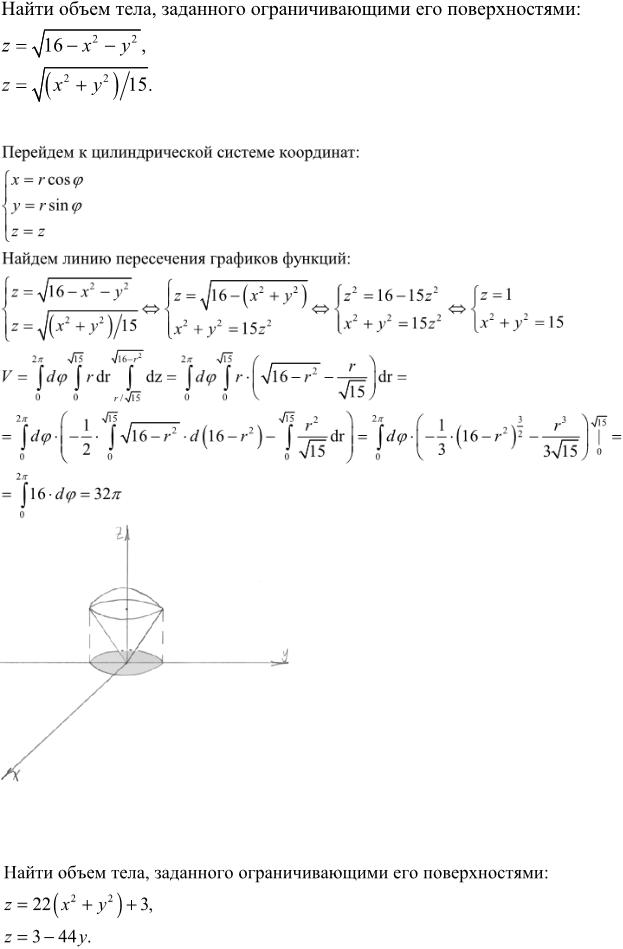Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью $$(x^2+y^2+z^2 )^3=\frac $$ с плотностью $z=0$ $(z \ge 0)$.
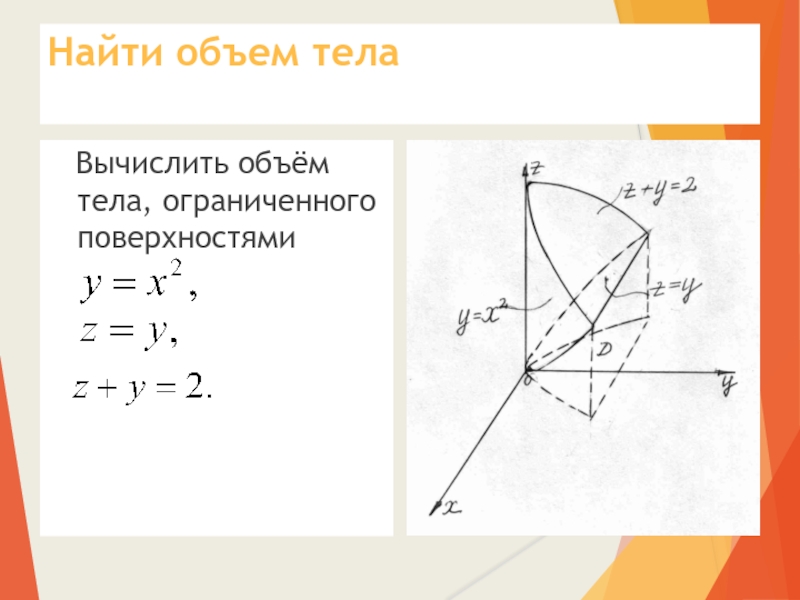Найдите объем тела, ограниченного поверхностями, заданными уравненинями `x^2+y^2=1,x^2+y^2=z,z=0`. Для решения задач необходимо зарегистрироваться.
Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми. Решение от преподавателя: Не нашли нужного вам решения? Оставьте заявку и наши авторы быстро и качественно помогут …
Найти объем тела, ограниченного поверхностями . Решение. Сначала построим основание заданного тела. Поверхность ограничена параболой и прямой y = 2. Выберем порядок …
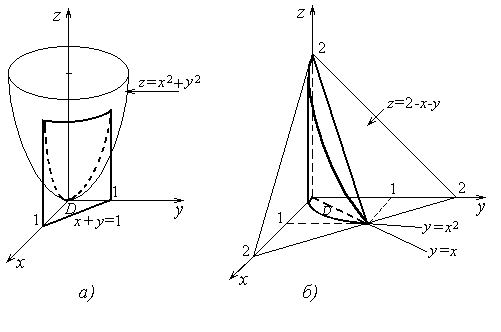
Найти объем тела ограниченного поверхностями: z=4-x^2-y^2, z=0 Решение: **Задание относится к предмету математики, а именно к разделу аналитическая геометрия и …
Решение: Это задание из раздела математического анализа, где требуется вычислить объем тела в трехмерном пространстве. Для решения задачи нахождения объема …
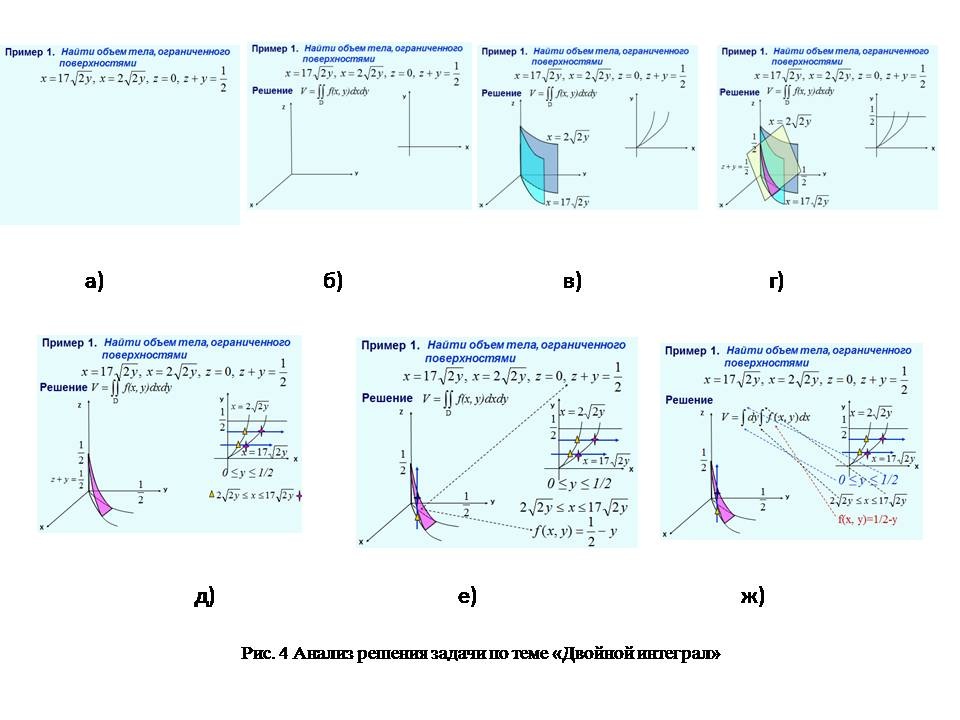Данный калькулятор предназначен для вычисления объема тела, ограниченного поверхностью. Он прост в использовании и не требует специальных навыков.
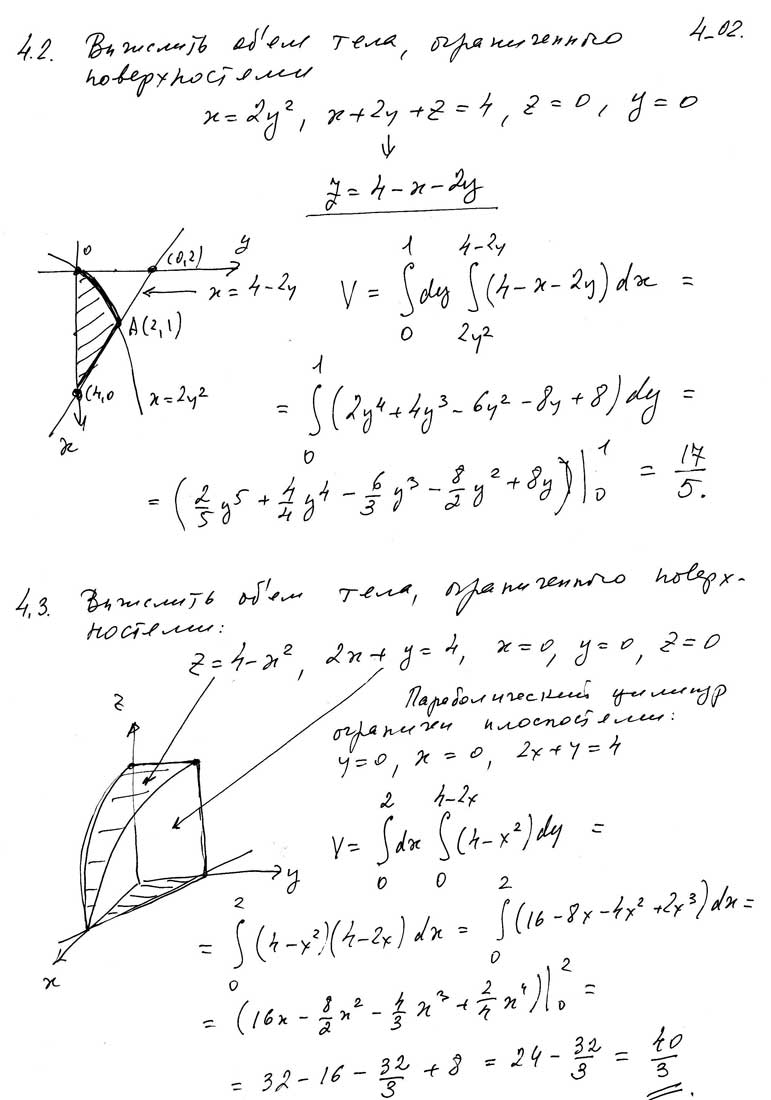Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями: $$z=2-x, z=0, y=\sqrt{x}, y=\frac{1}{4}x^2.$$
Данный калькулятор поможет вам вычислить объем тела, ограниченного поверхностями. Для этого вам потребуется знать длину, ширину и высоту тела.
Найти объём области, ограниченной поверхностями x 2 + y 2 + z 2 = R 2, ( x 2 + y 2)3 = R 2( x 2 + y 2). Решение: Первая поверхность - сфера, вторая - цилиндрическая - с …
Чтобы найти объем тела, ограниченного указанными поверхностями, можно использовать тройной интеграл. Первое уравнение x 2 = 4 y задает параболоид в плоскости X-Y. …
С помощью тройного интеграла найти объём тела, ограниченного поверхностями. Решение: проекция здесь несложная, но вот над порядком её обхода нужно подумать. Если …
Найти объем тела, ограниченного поверхностями. V : z ≥ x 2 + y 2, z = 4. Ответ. Найдем объем тела, ограниченного плоскостью z = 4 и параболоидом вращения …
Еще по теме:
Еще по теме:
