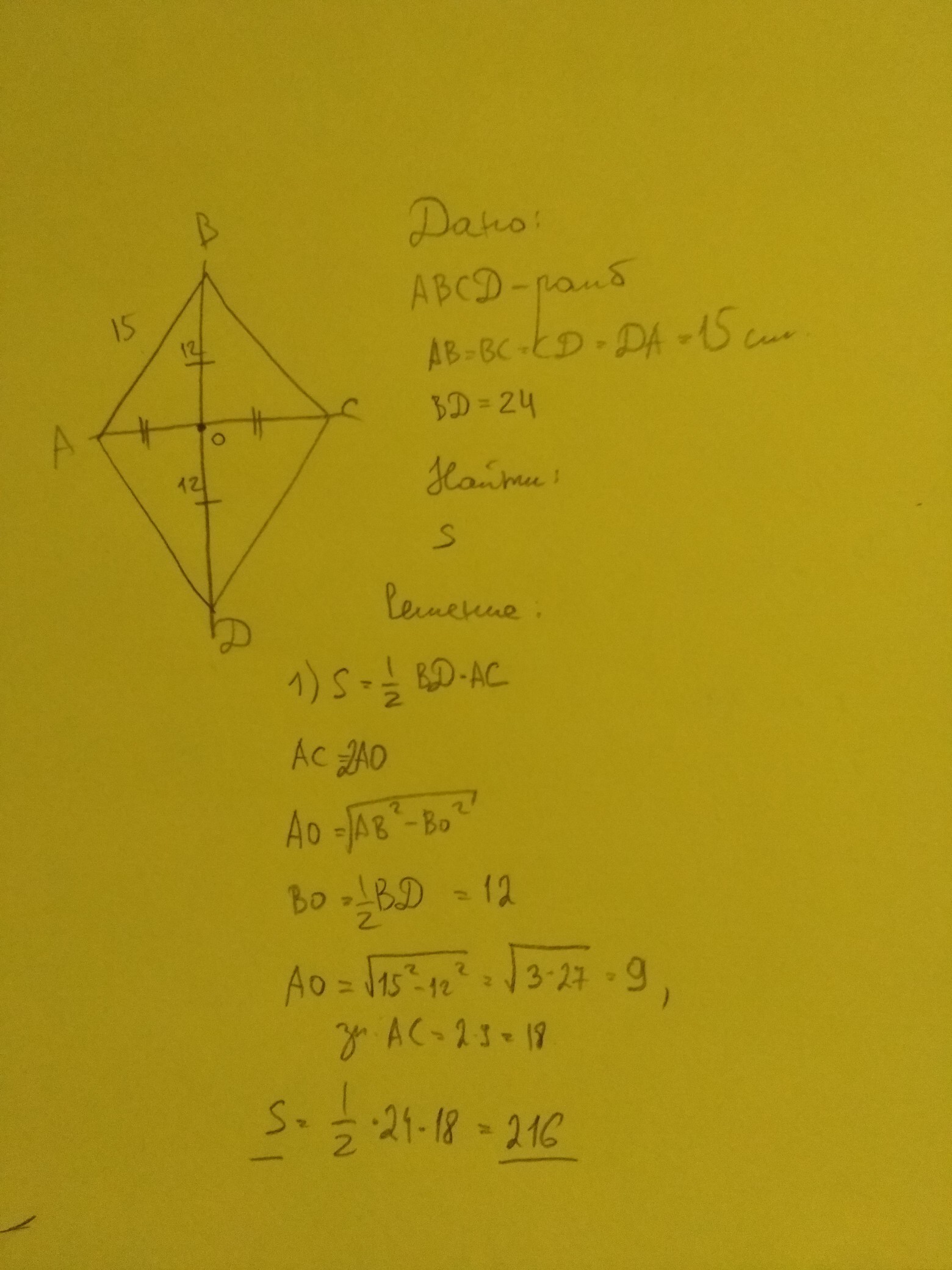Подробный ответ из решебника (ГДЗ) на Задание 493 по учебнику Л.С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. Учебник по геометрии 7-9 классов. 2-е издание, Просвещение, 2014г.
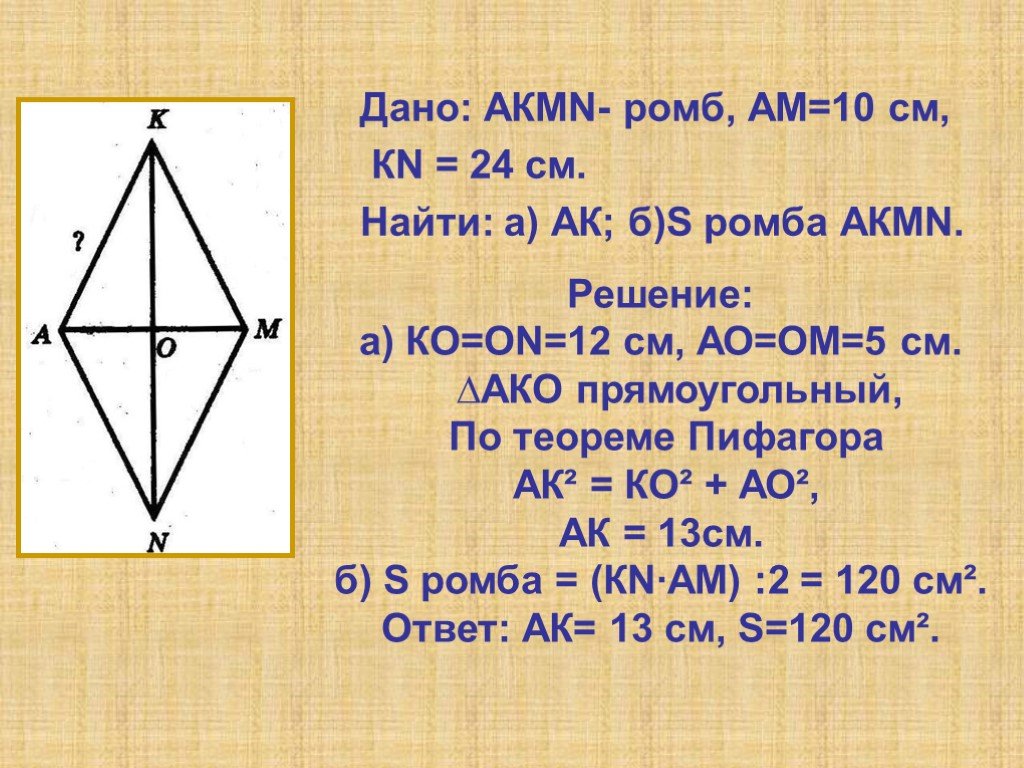
Вроде как диагонали к тому же пересекаются под прямым углом. Значит квадрат стороны ромба равен 25+144=169. Следовательно сама сторона равна 13 см.
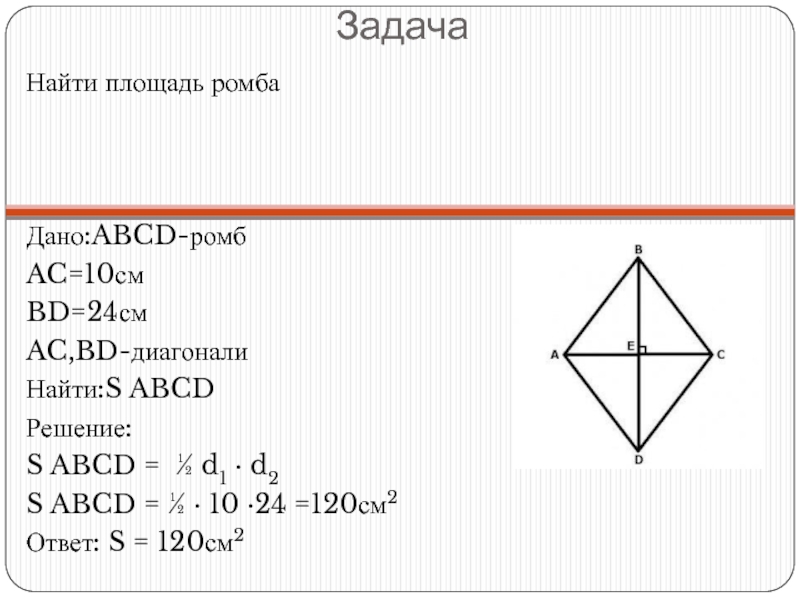
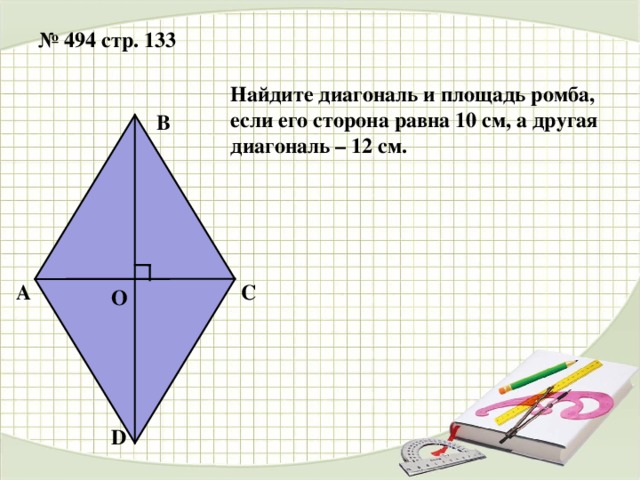
Диагонали ромба равны 10 и 24 см. Вычислите площадь ромба и его периметр. Решение: диагонали ромба взаимноперпендикулярны и точкой пересечения делятся пополам, …
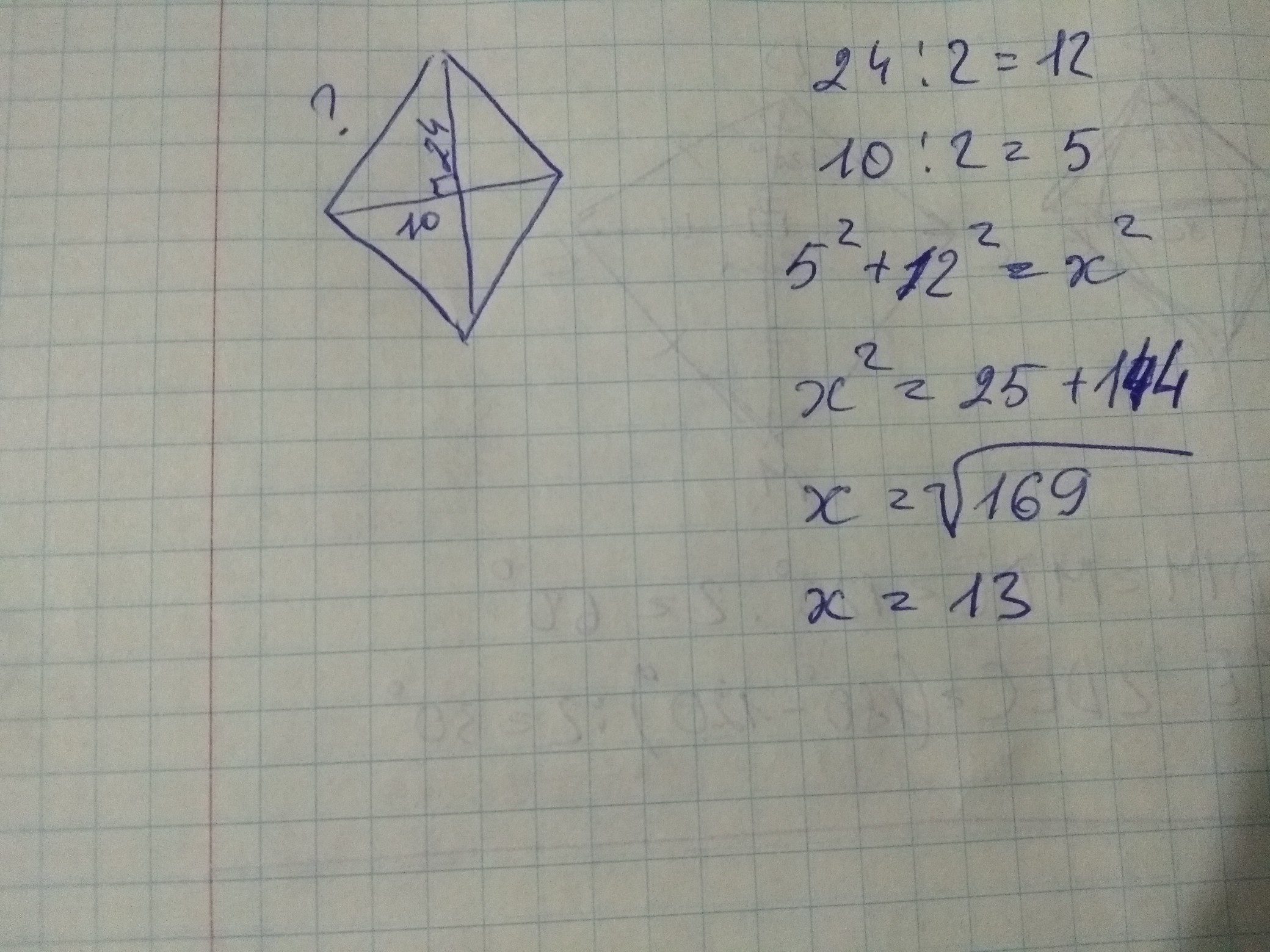Диагонали ромба пересекаются под углом в 90 градусов и делятся пополам, стало быть сторона ромба по теореме Пифагора равна корень квадратный из 12*12+5*5, т. е. из …
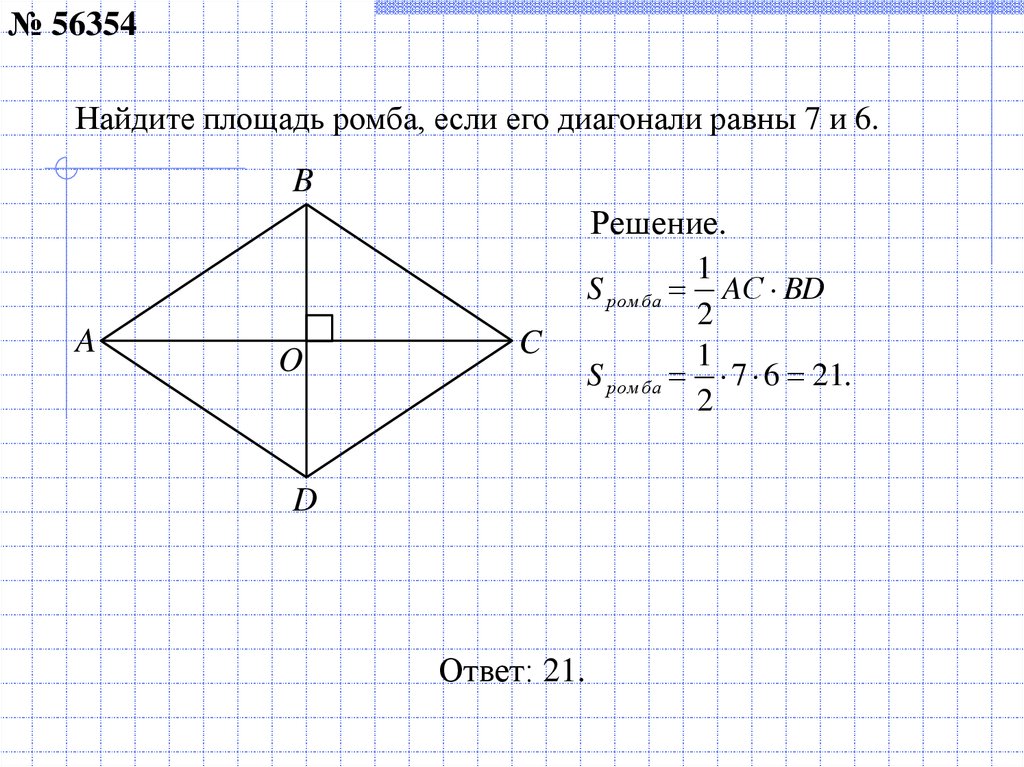
Площадь ромба равна половине произведение его диагоналей. Sавсд = АС * ВД / 2 = 10 * 24 / 2 = 120 см 2 . Диагонали ромба, в точке их пересечения, делятся пополам и …
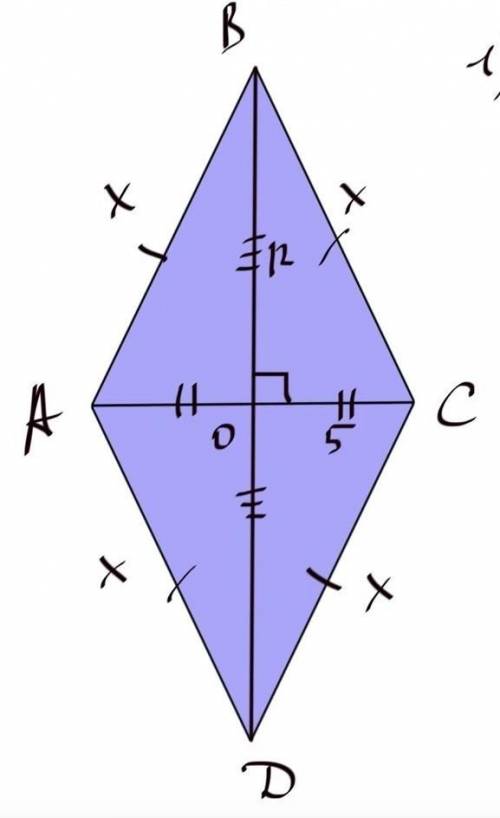В ромбе диагонали пересекаются под прямым углом и делятся пополам. По теореме Пифагора находим стороны : а² = 5² + 12². а = √169 = 13. p = 13 * 4 = 52. s = (10 * …
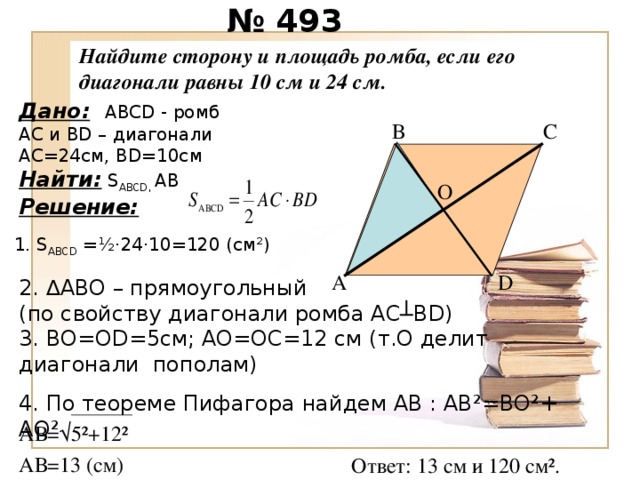
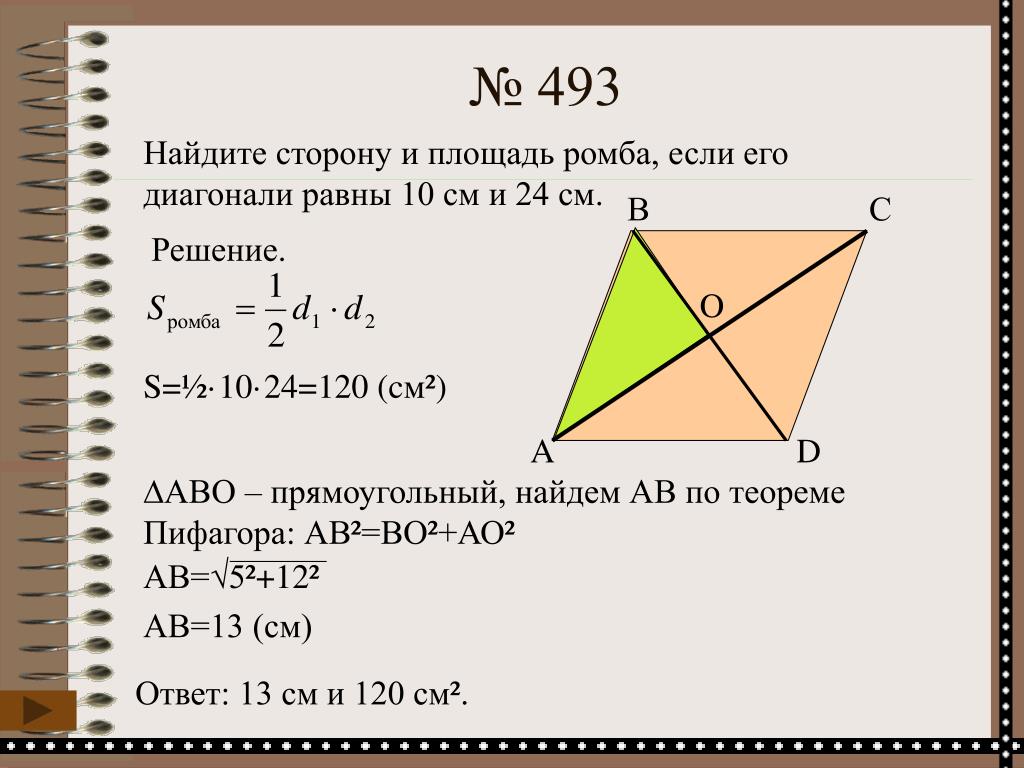
Ответы (1) 1) Находим площадь ромба АВСД : S = d1 * d2 / 2 = 10 * 24 / 2 = 120 (см кв) 2)Находим АВ - сторону ромба. Для этого рассмотрим прямоугольный …
Если диагонали ромба равны 10 см и 24 см, а его сторона 13 см, то высоту можно найти следующим образом: Назовем высоту ромба «h».
Диагонали ромба равна 24 см и 70 см. Найдите углы ромба.
Диагонали точкой пересечения делятся пополам. Нам нужно найти AB. У нас получился тр-ник прямоугольный ABO.
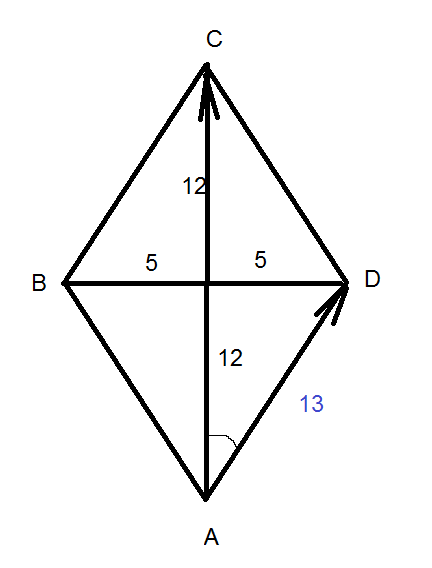
Пусть, АС и bd- диагонали ромба. О- точка пересечения диоганалей. АО=ОС=10/2=5 ВО=do=24/2=12 АВ=√(144+25)=√169=13 p=4ab=4*13=52
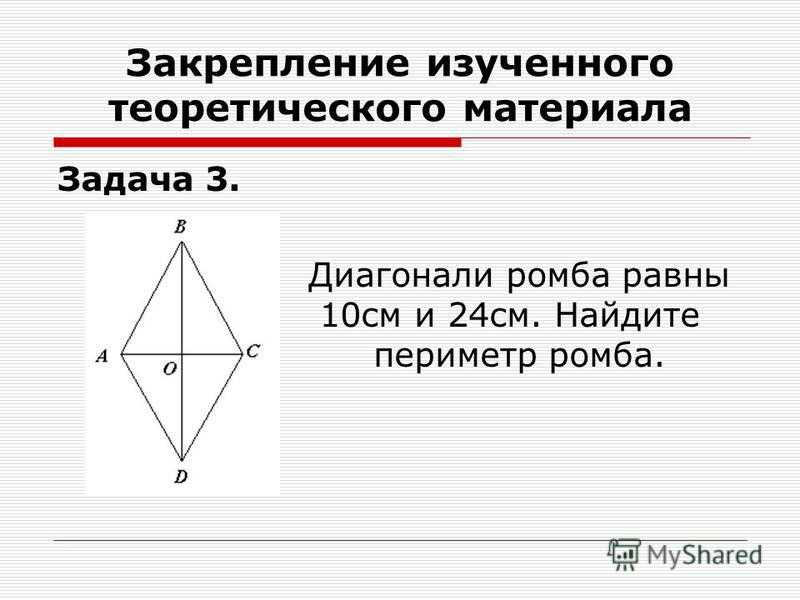Из точки пересечения диагоналей проводишь прямую параллельную стороне ромба, которая равна стороне ромба, как параллельная между параллельными и точкой …
Диагонали ромба, в точке их пересечения, делятся пополам и пересекаются под прямым углом. Тогда ОВ = ОД = ВД / 2 = 10 / 2 = 5 см, АО = СО = АС / 2 = 24 / 2 = 12 см, а …
Онлайн калькулятор и формулы для вычисления площади ромба через диагонали, длину стороны и высоту, полупериметр и длину стороны, а также через длину стороны и …
Представлен ромб со стороной 4 см. Одна из диагоналей ромба равна 4 см. Найти площадь ромба.
Площадь ромба равна половине произведения его диагоналей:s = (ac · bd) / 2 s = (10*24) / 2 = 120 см сторона является гипотенузой прямоугольного треугольника со сторонами …
Еще по теме:
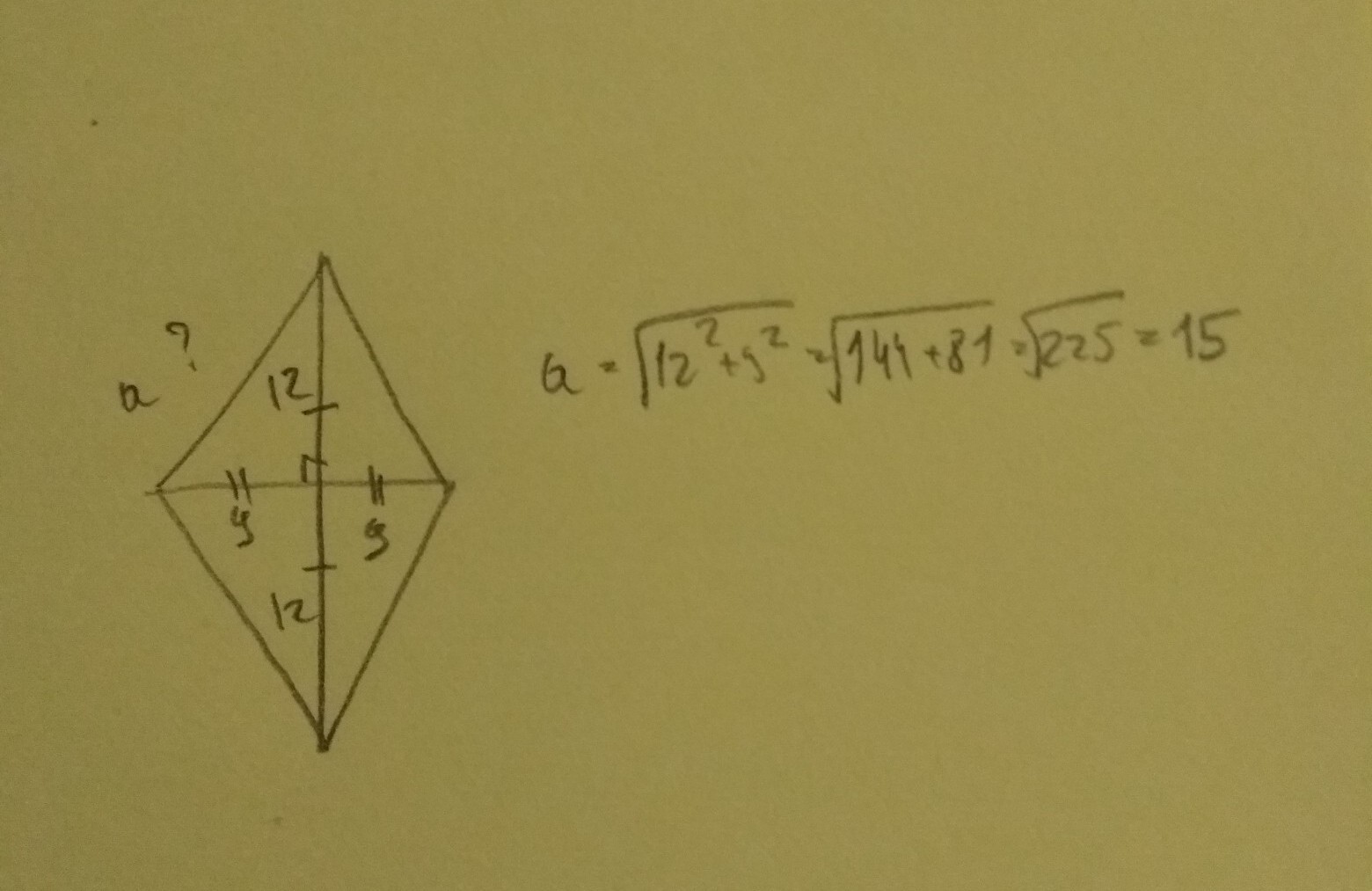
Еще по теме:
