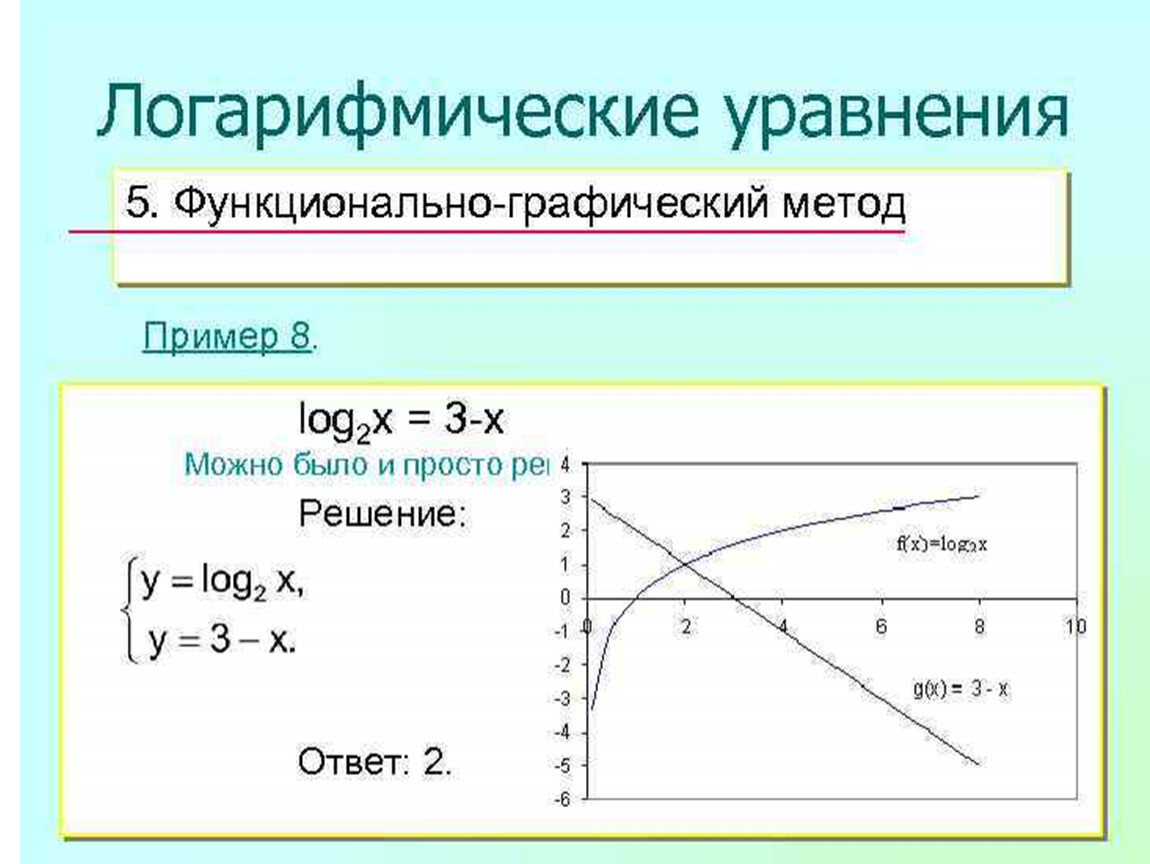
На этой странице вы узнаете, что такое логарифмические функции, а также как их представить на графике. Кроме того, вы увидите все его характеристики, способы …
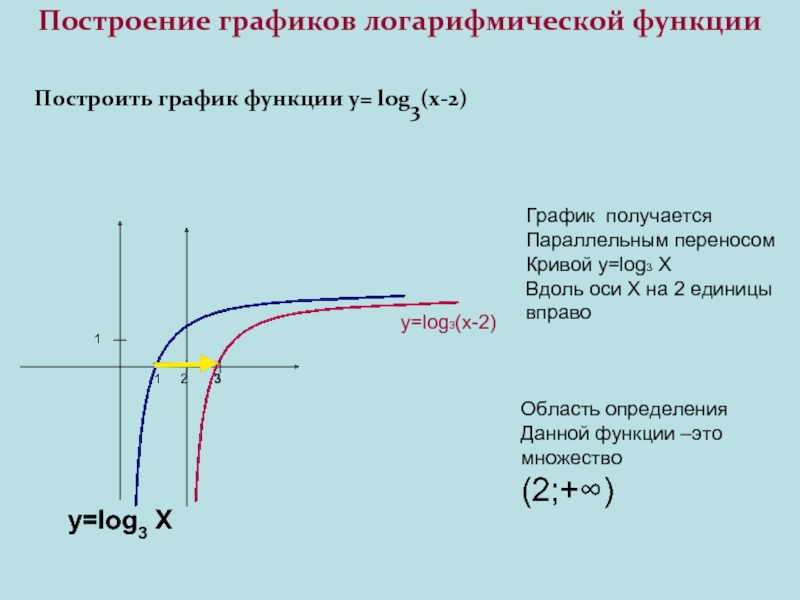
Для построения графика логарифмической функции необходимо следовать нескольким простым шагам. Во-первых, определите, какой вид логарифмической функции вам …
Содержание: Логарифм числа. Основное логарифмическое тождество. Свойства логарифмов и формулы логарифмирования. Логарифмическая функция. Понятие …
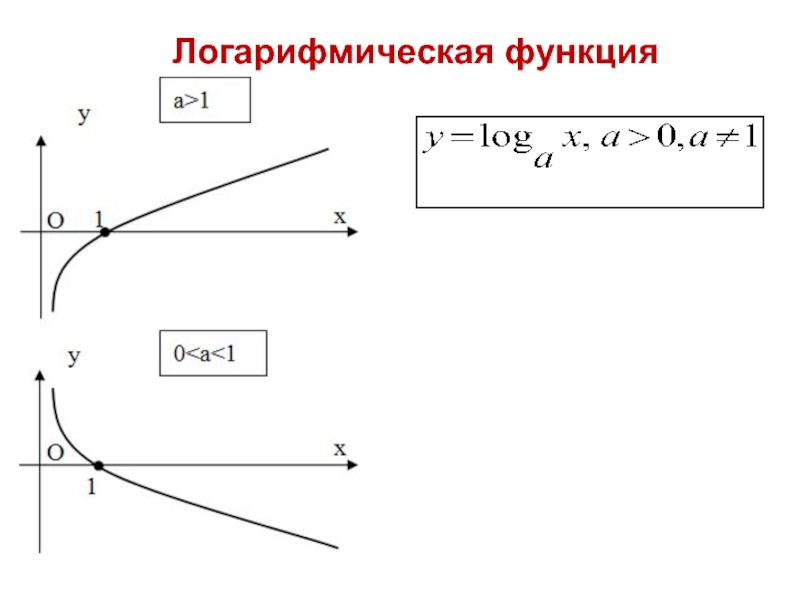
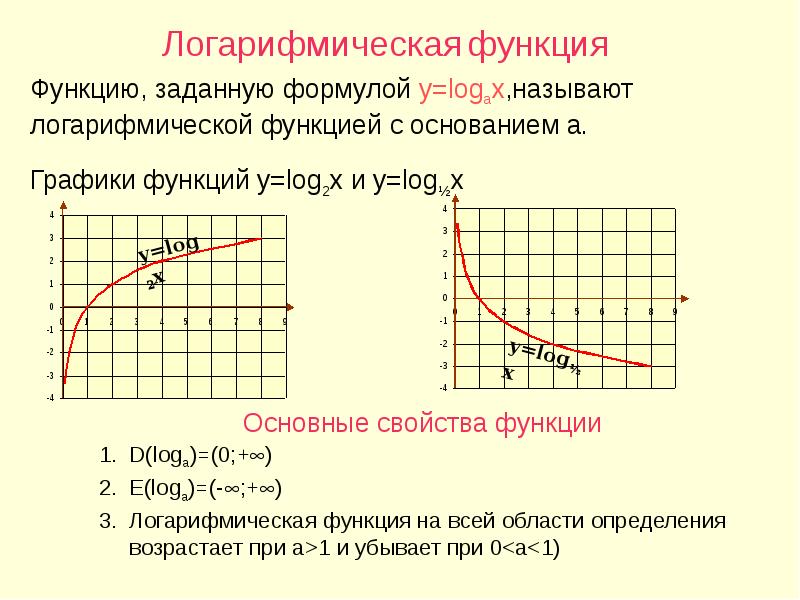
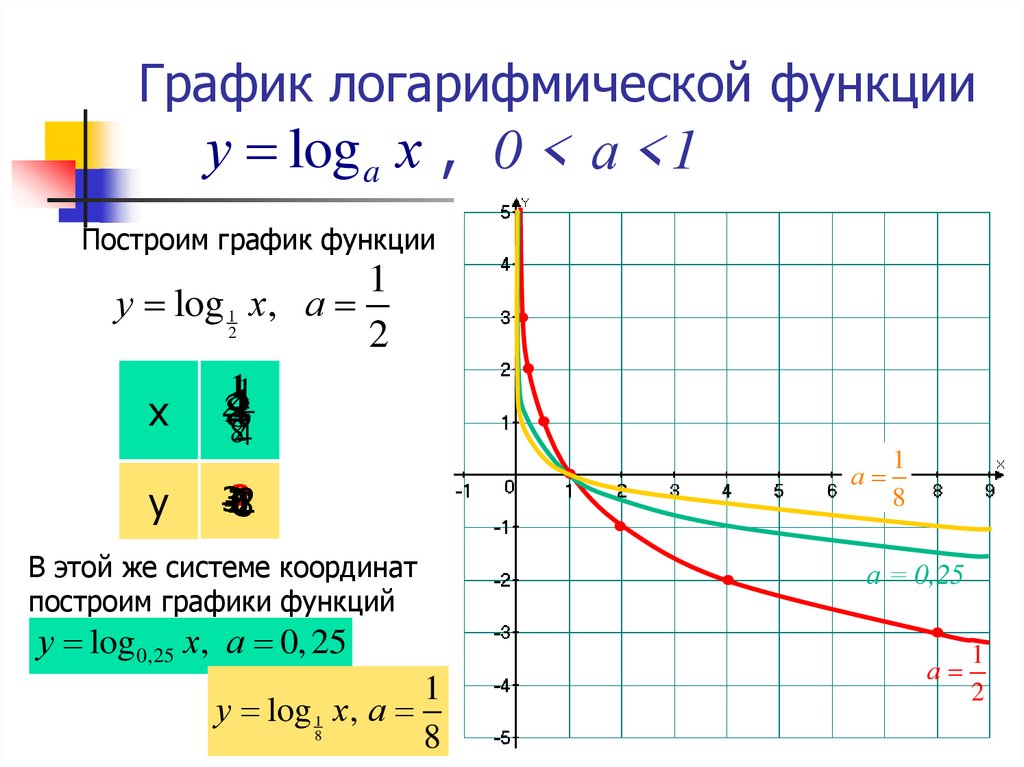Логарифмическая функция. Функция $y=log_a x$ (где $a>0$, $a\neq 1$) называется логарифмической функцией с основанием $a$. …
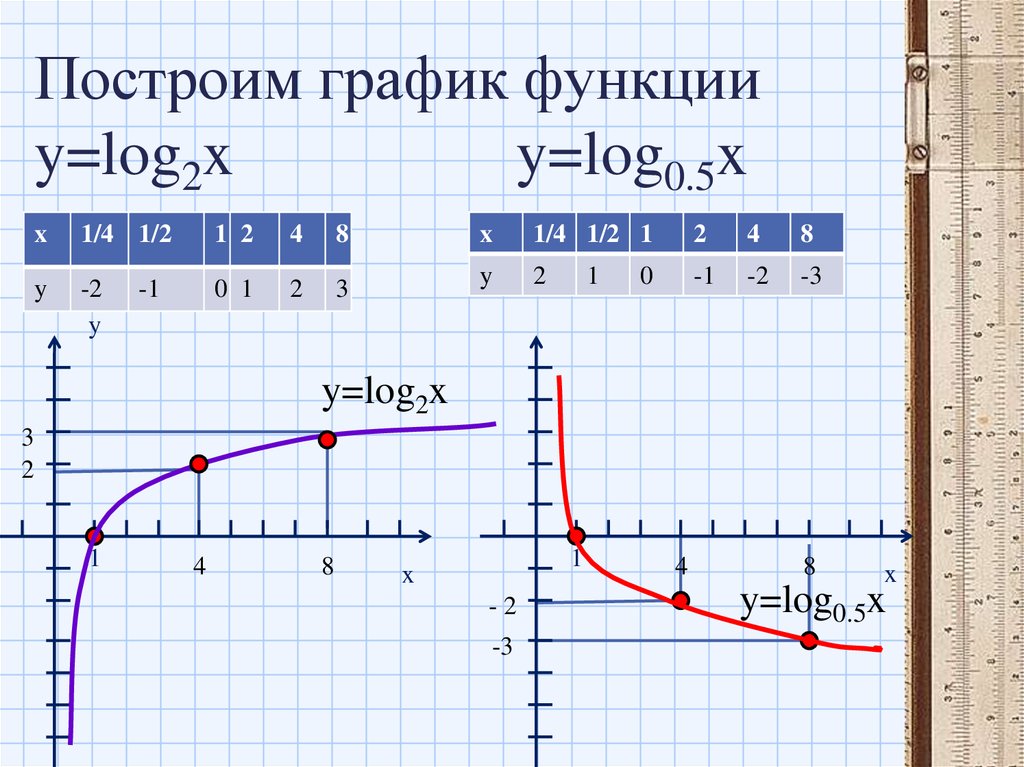
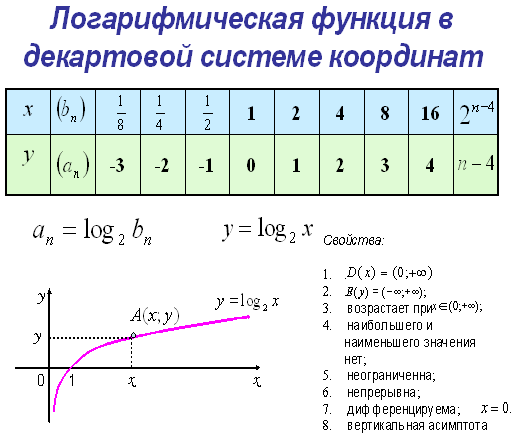
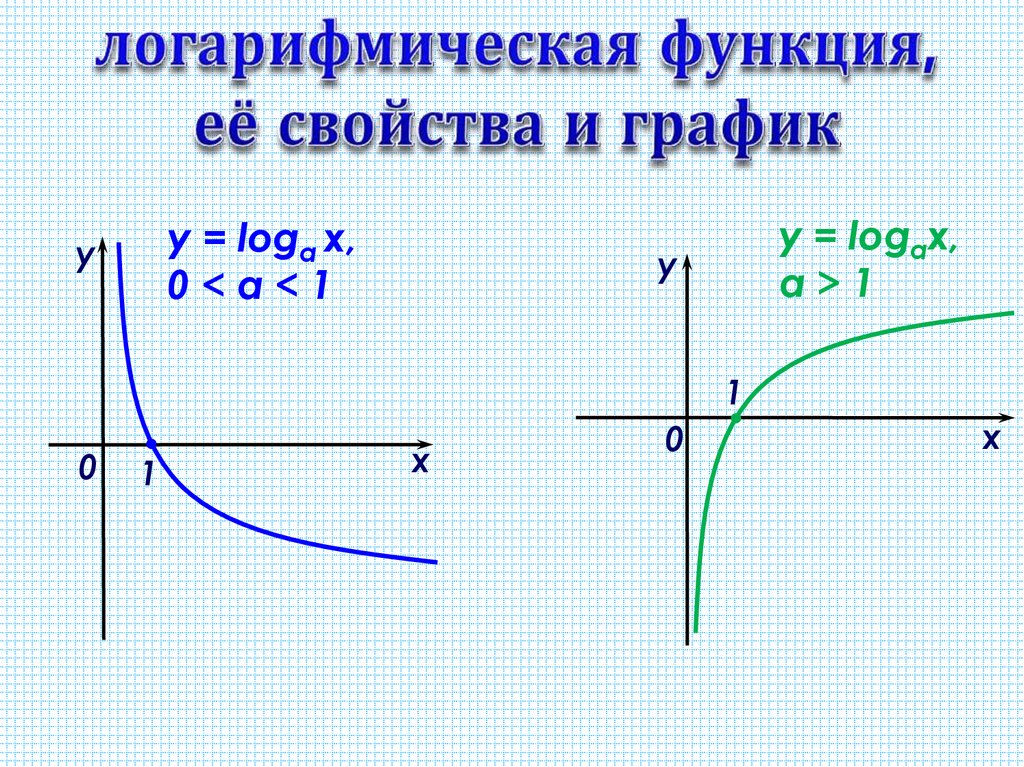Для начала необходимо вспомнить свойства простого логарифма и ее функции. С их помощью нужно построить таблицу для конкретных значений x и y.
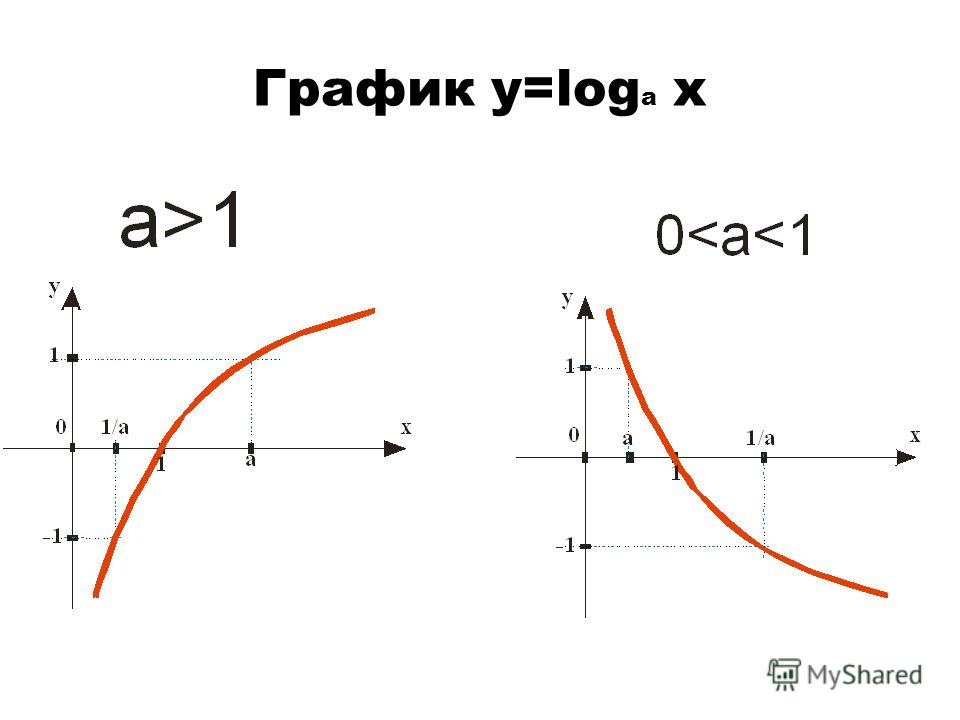
Логарифмическая функция – это функция вида , где а – заданное число, а>0, а≠1. Наша задача – научиться строить и исследовать графики логарифмических …
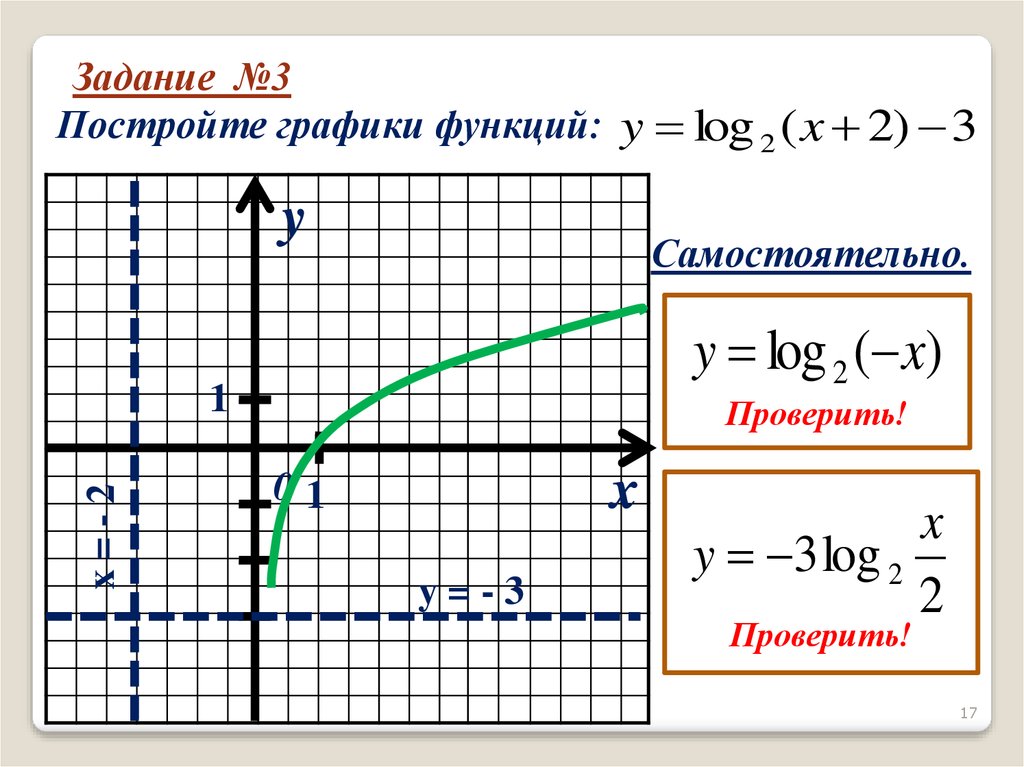
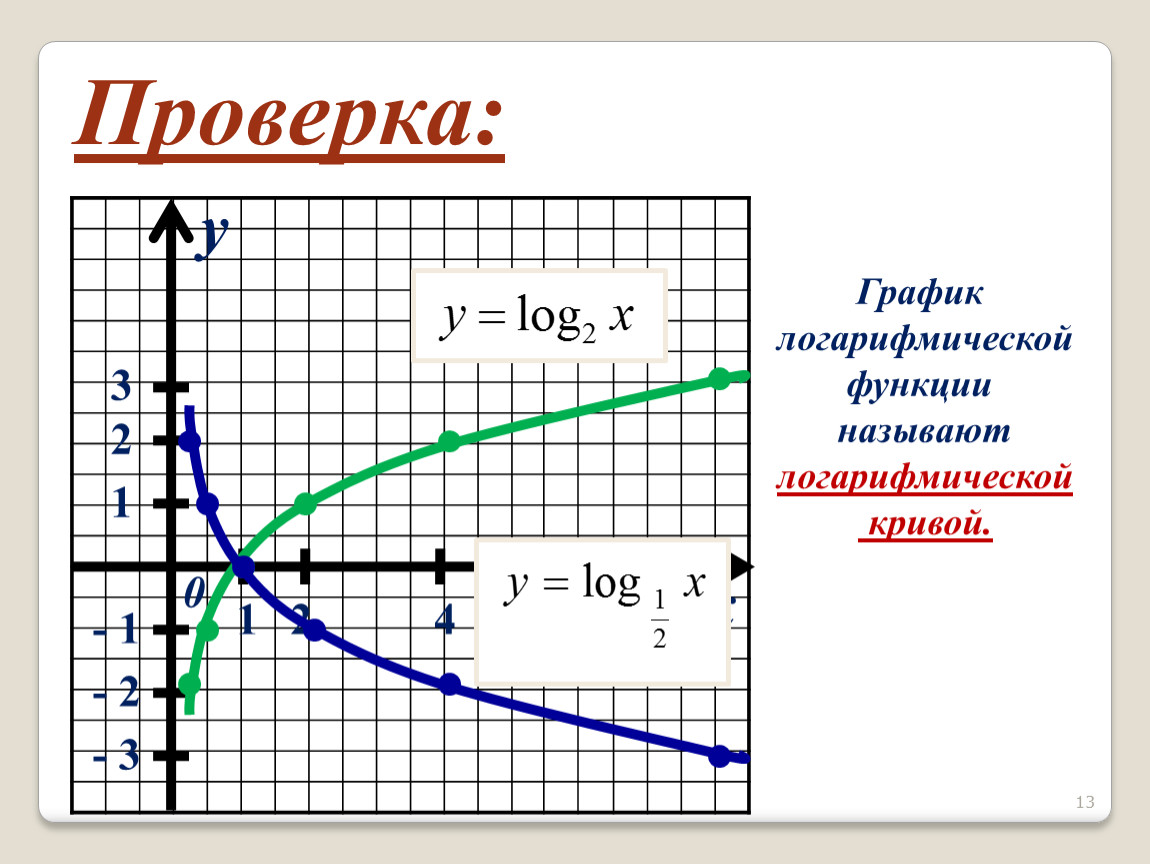Графики логарифмических функций можно строить как вручную, так и с использованием специальных компьютерных программ.
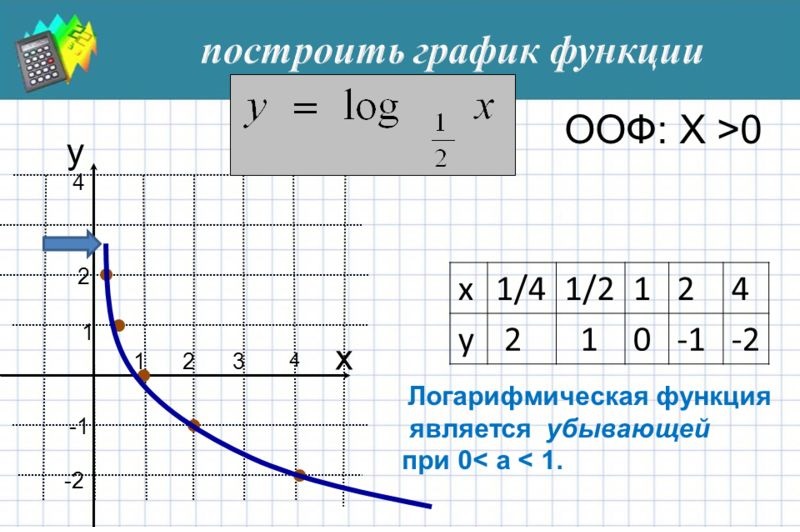В этом видео показано, как построить график логарифмической функции. Это видео - русская версия видео «Graphing Logarithmic Functions» Академии Хана (.
Этот создатель графиков логарифмических функций позволяет вам построить логарифмическую функцию или сравнить график двух логарифмических функций с …
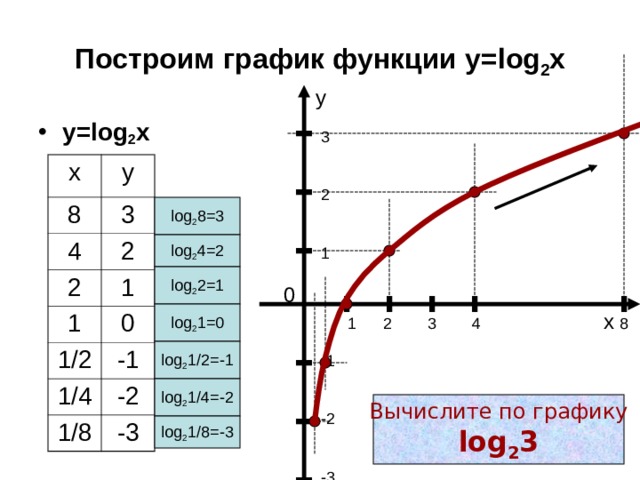В этой статье мы рассмотрим, как построить логарифмический график и как его использовать для анализа данных. Что такое логарифмическая шкала?
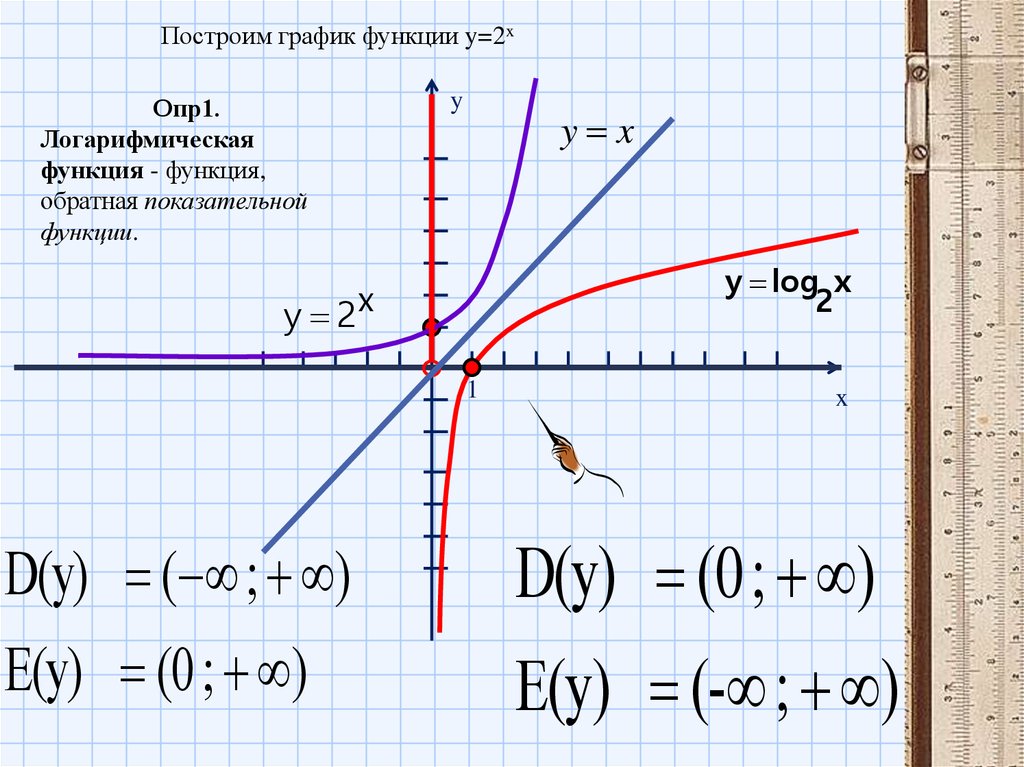
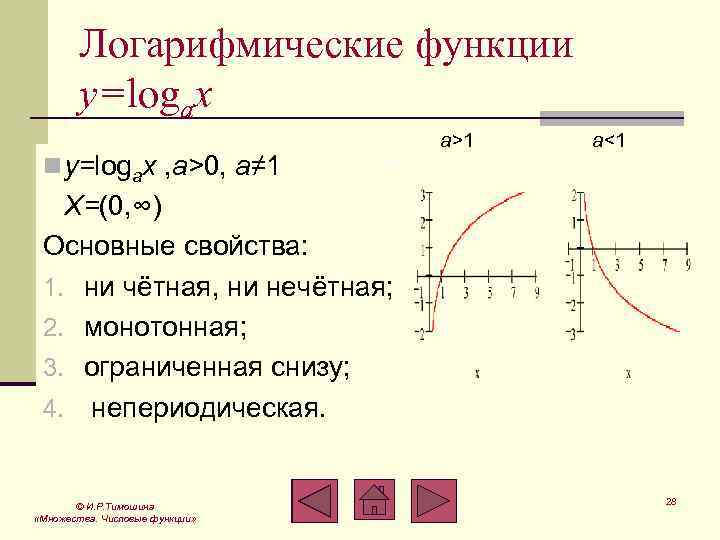
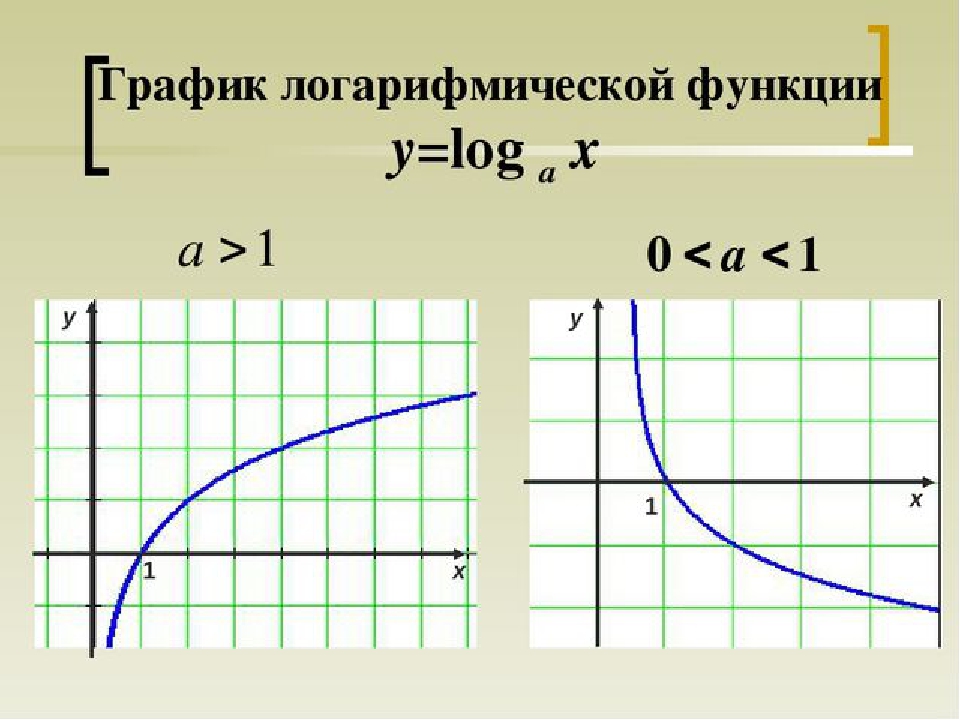Логарифмической функцией называется функция вида. y = log ax, где а - некоторое фиксированное положительное число, отличное от 1. Формула y = log ax выражает то же …
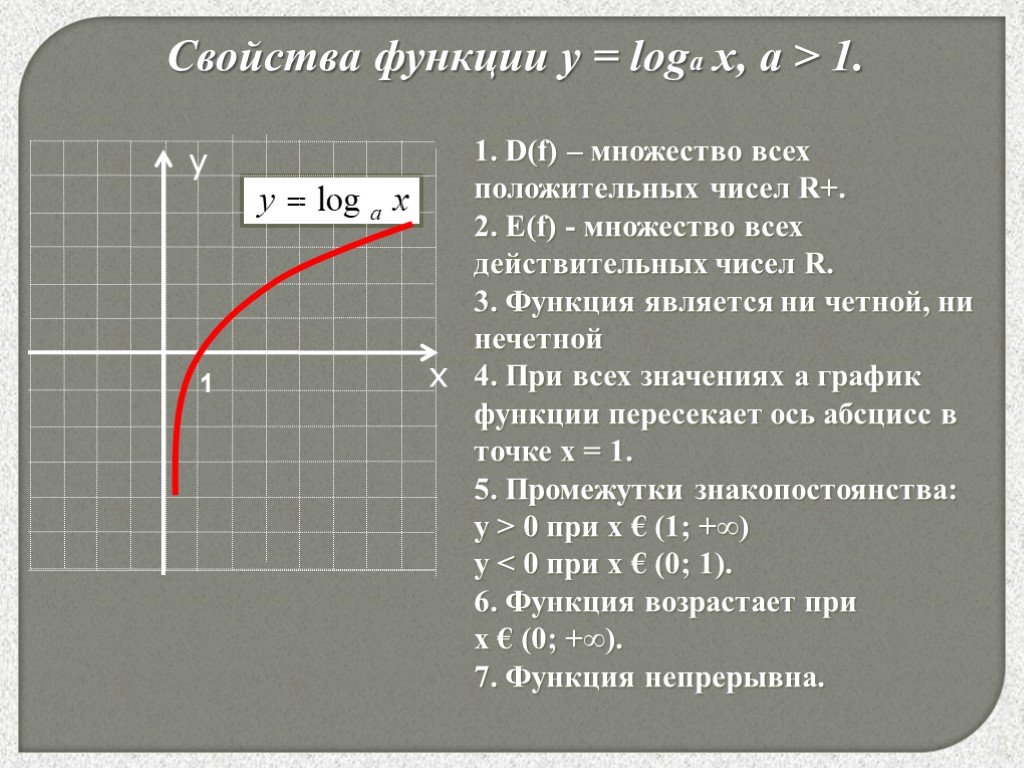
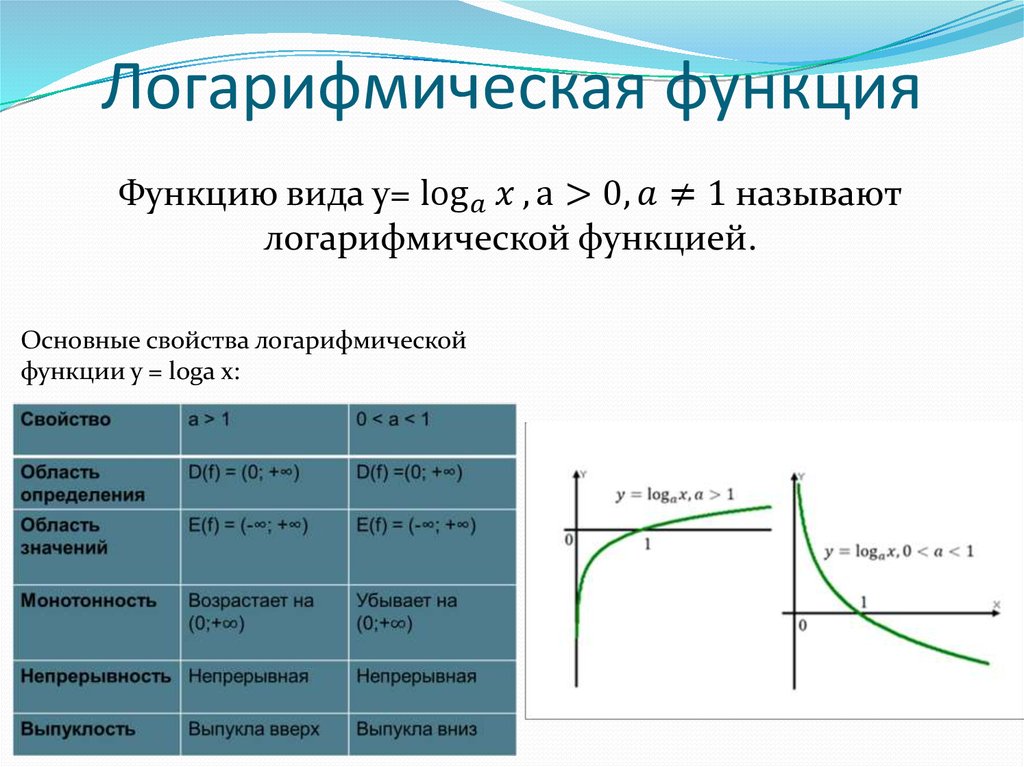
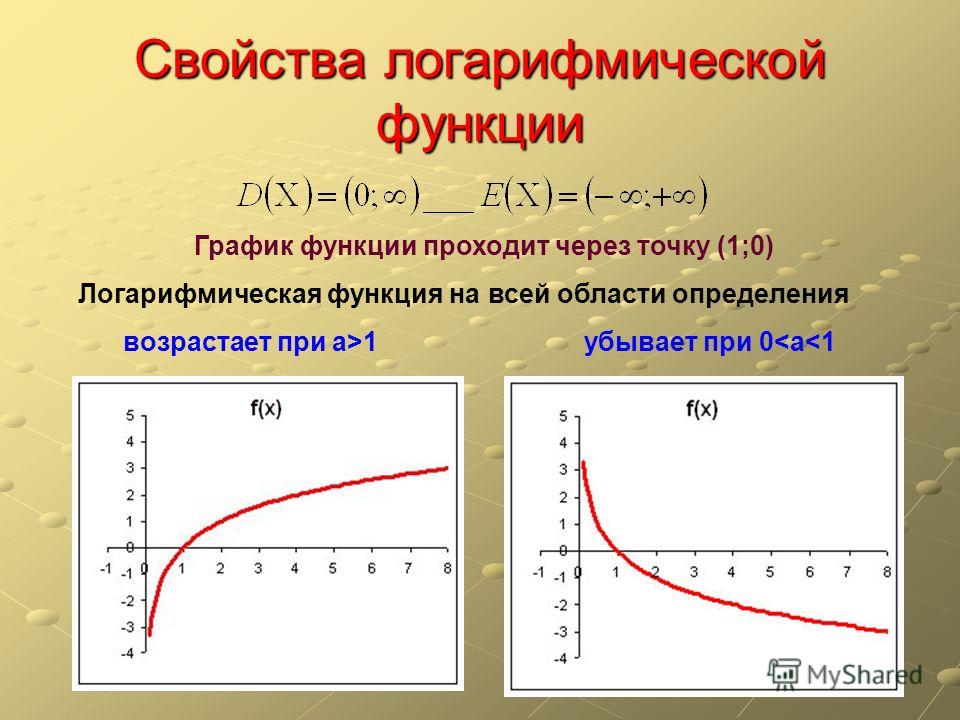
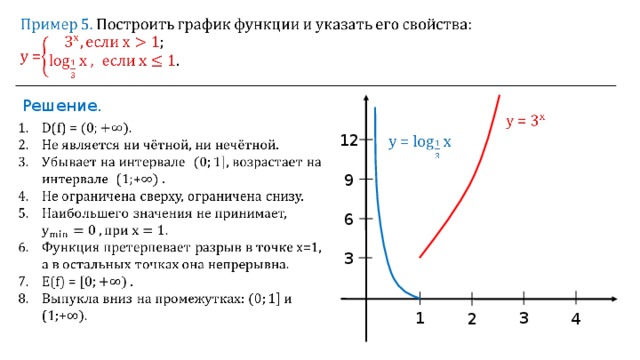
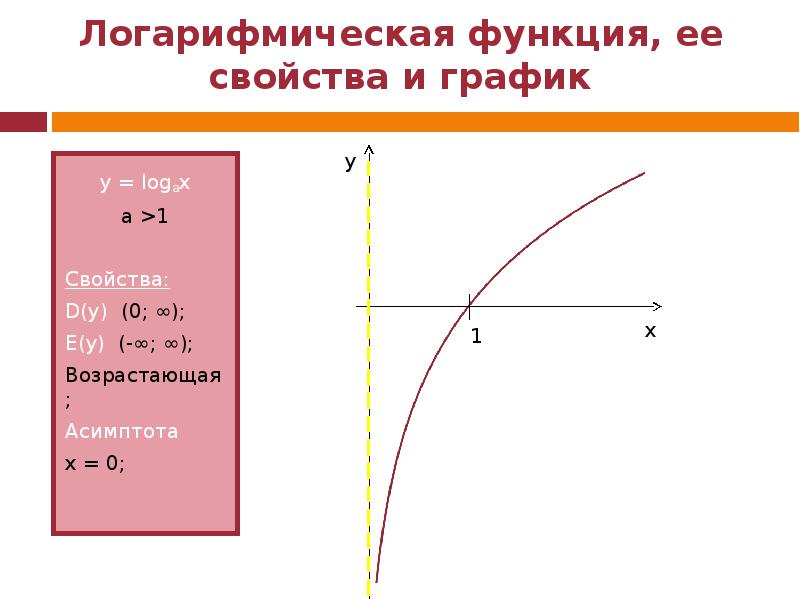
Логарифмическая функция - это функция вида y = log a x, x > 0, a > 0, a ≠ 1. Свойства логарифмической функции. Область определения: D (y): x ϵ (0; +∞). …
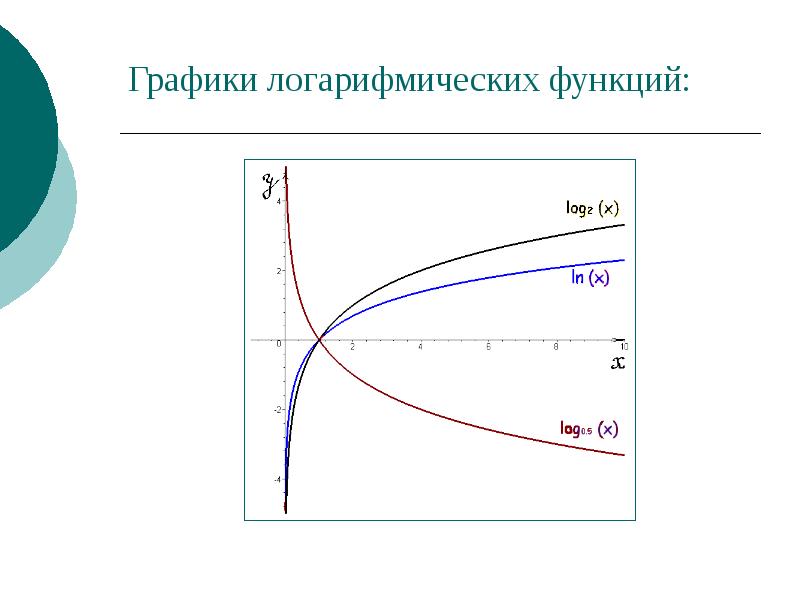
Графики логарифмических функций: y = ln(x), y = lg(x), y = log 5 (x) [ перейти к редактированию >> ] Вернутся к списку всех примеров построения графиков функций .
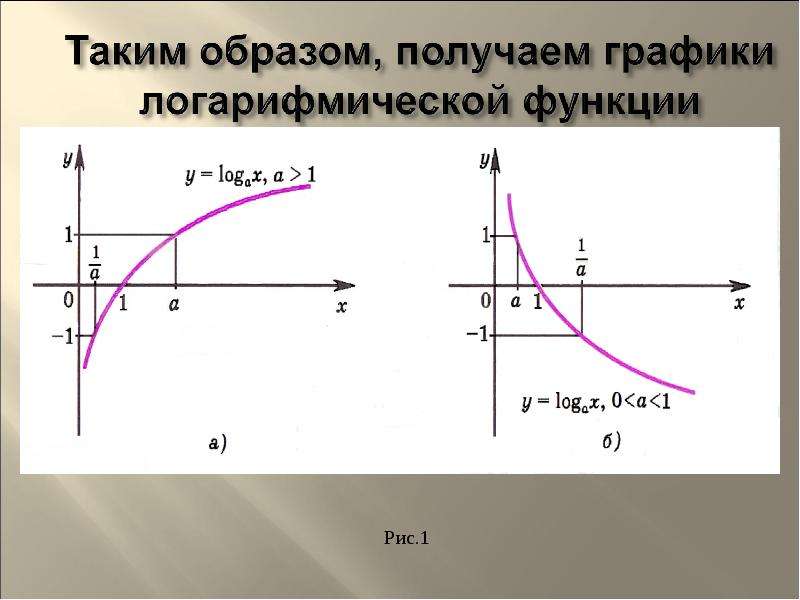
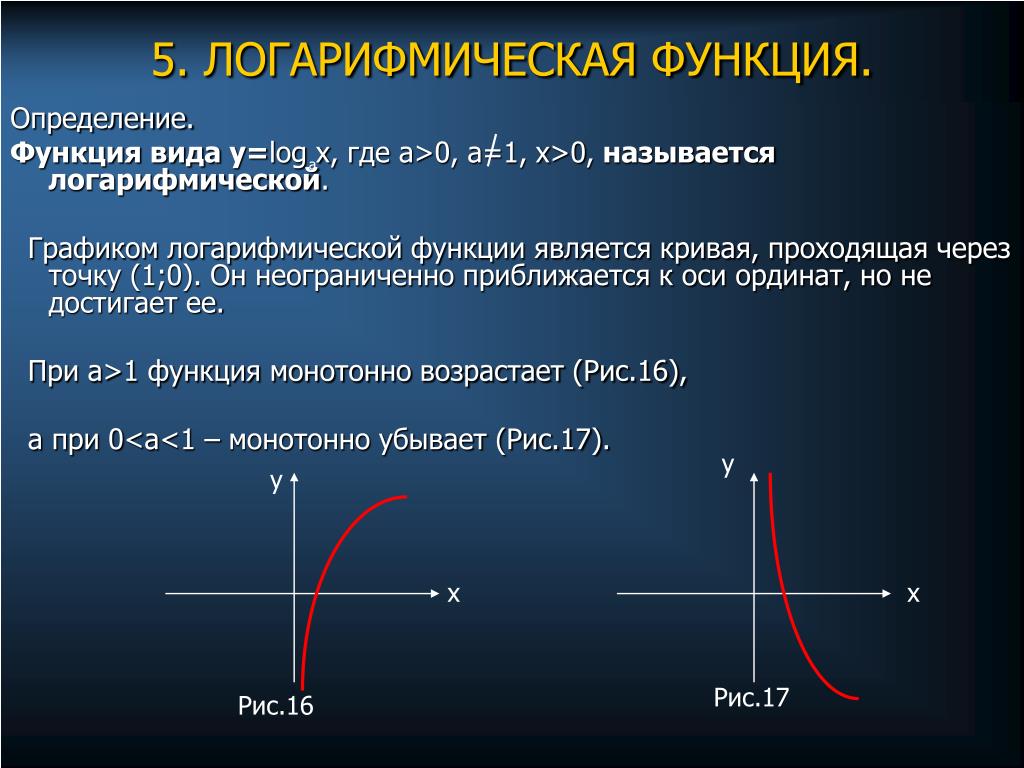
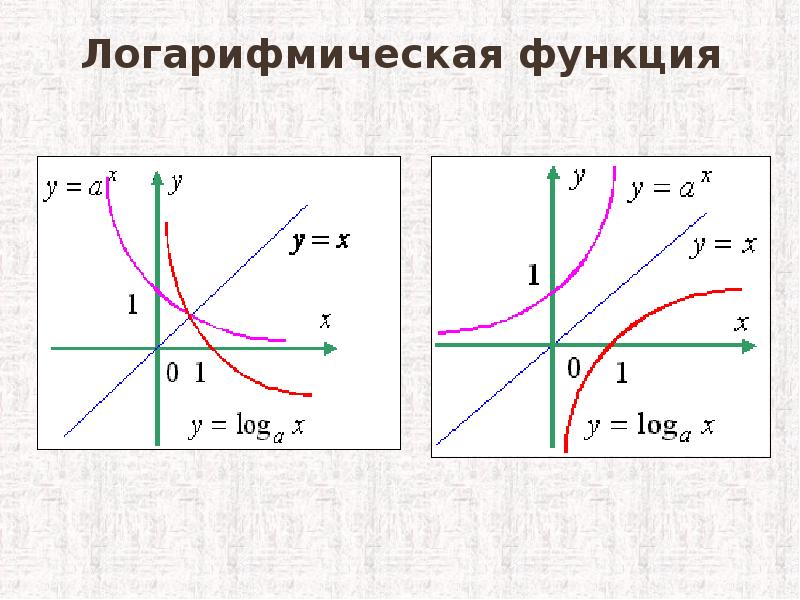
Логарифмическая функция и ее график. Логарифмической называется функция вида у = log a x, где а – заданное число, а > 0, а ≠ 1. Рассмотрим свойства …
Как самостоятельно разобраться в логарифмах. Как быстро и легко научиться решать логарифмы (решать логарифмические неравенства и уравнения)
Еще по теме:
Еще по теме:
