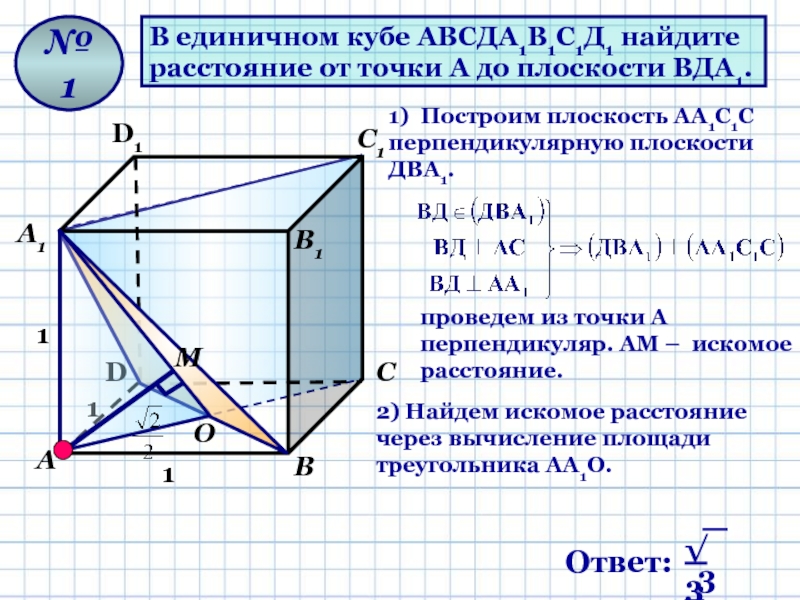
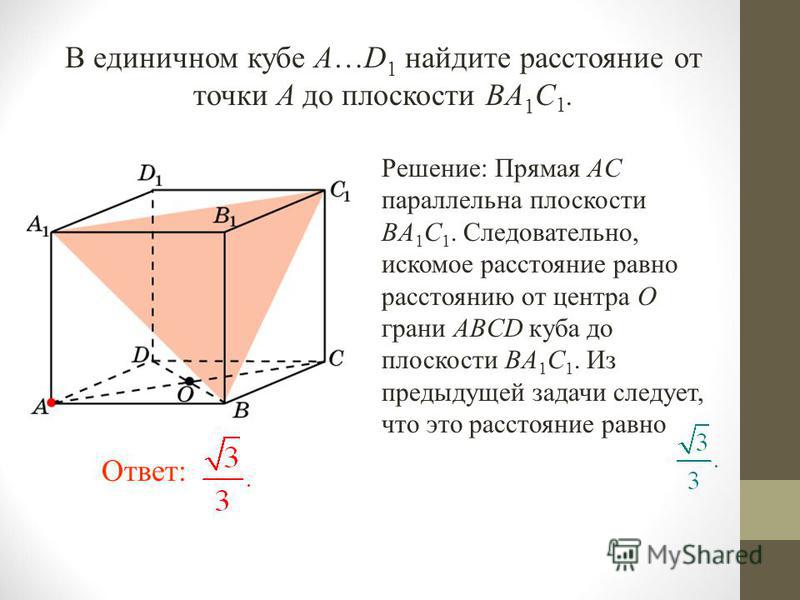
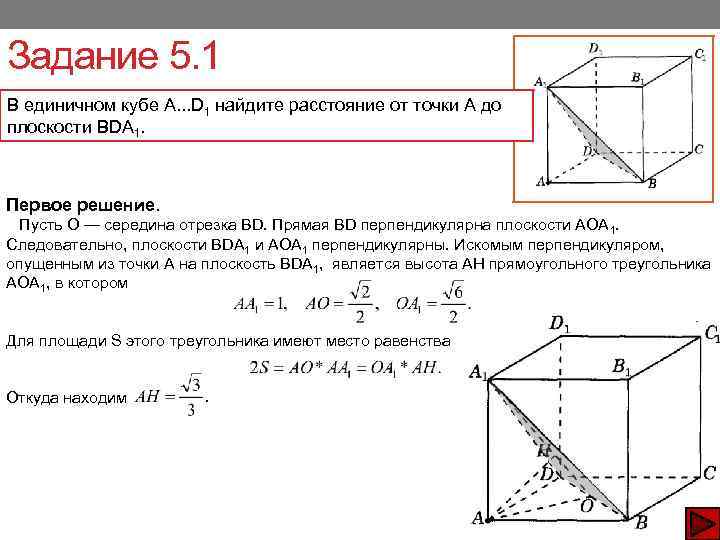
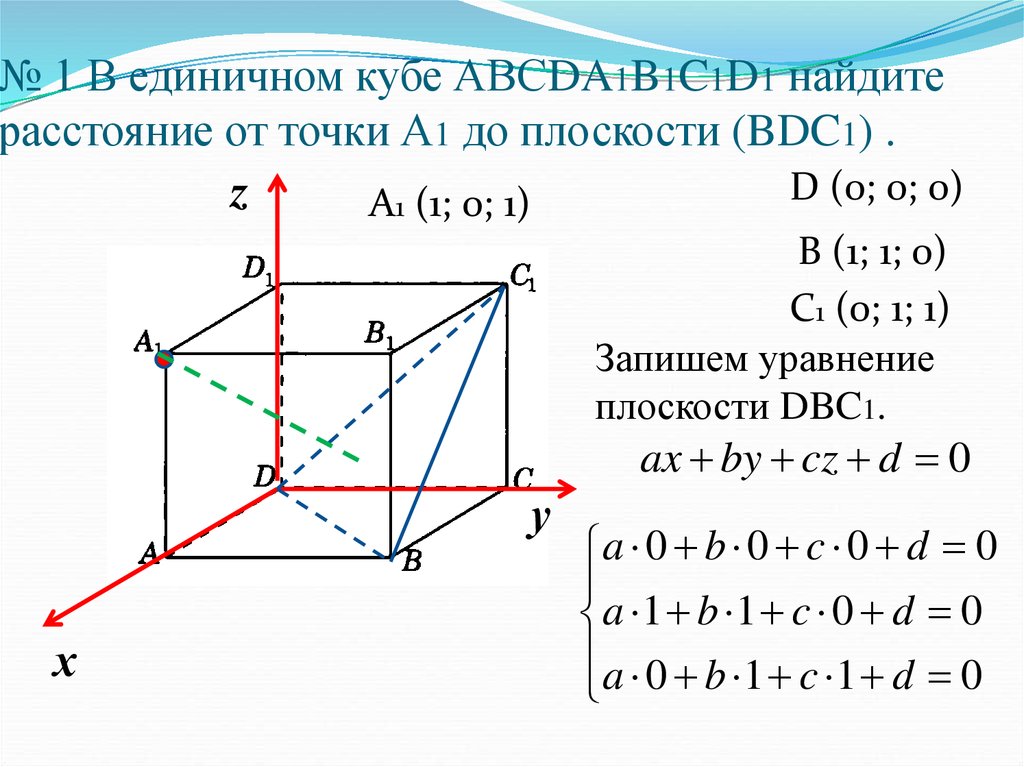
 В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки А до плоскости BDA1. - ответ на этот и другие вопросы получите онлайн на сайте Uchi.ru
В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки А до плоскости BDA1. - ответ на этот и другие вопросы получите онлайн на сайте Uchi.ru
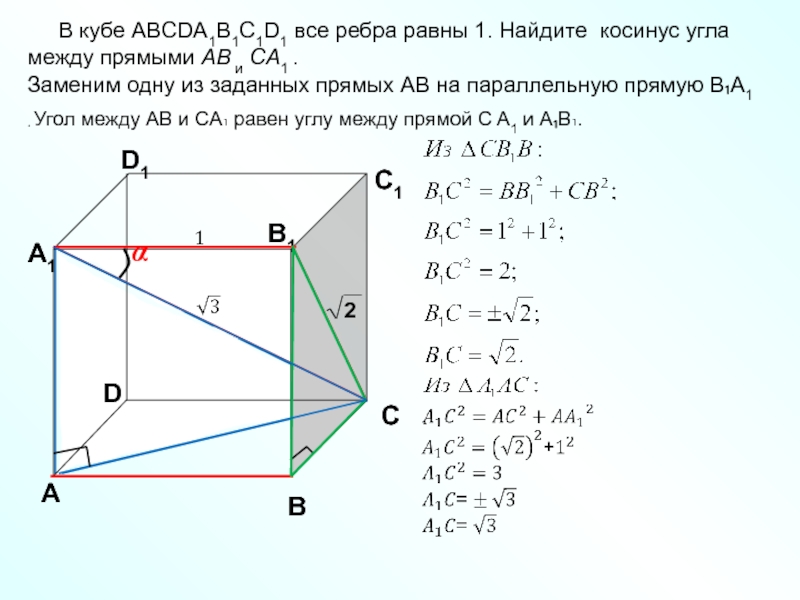
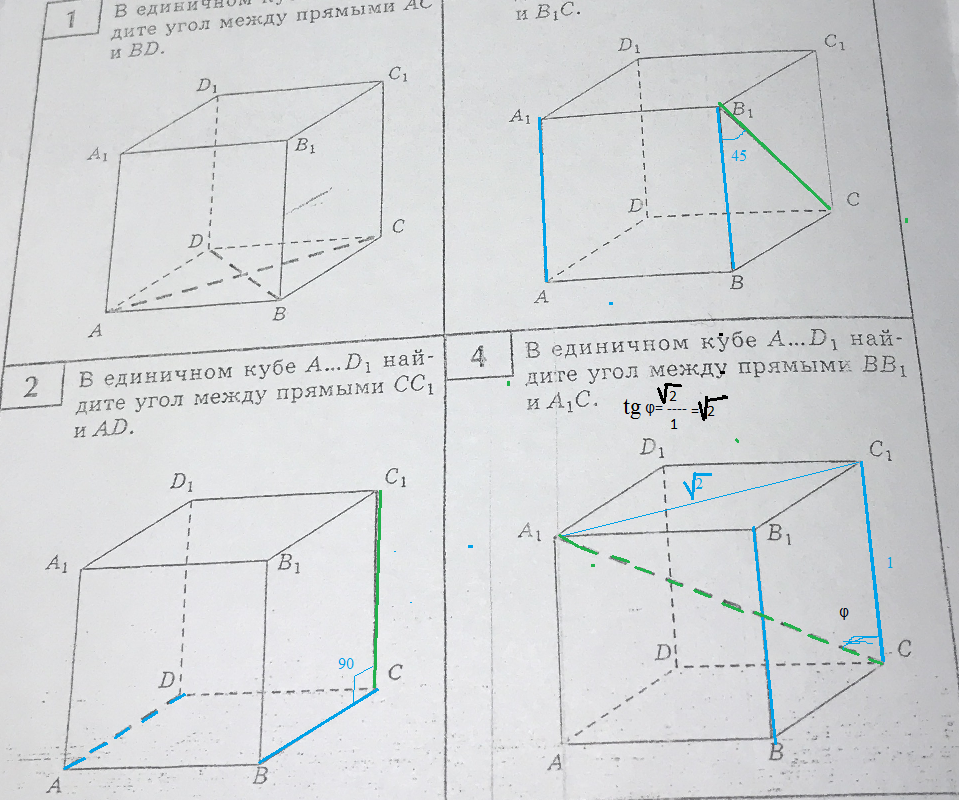
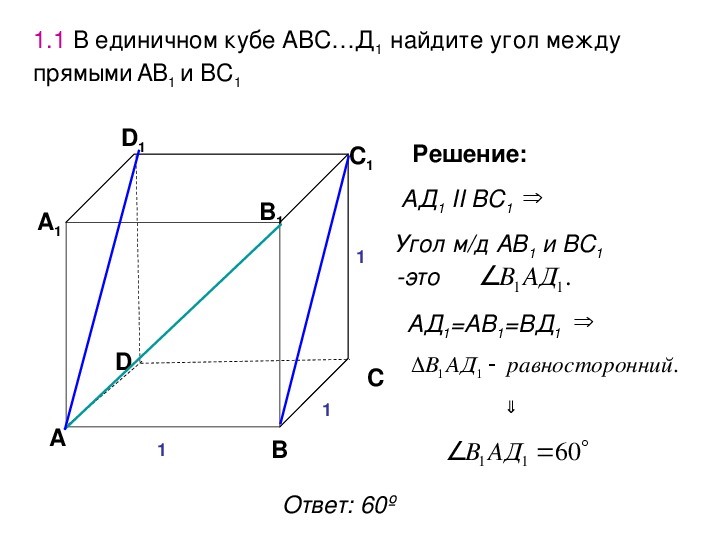
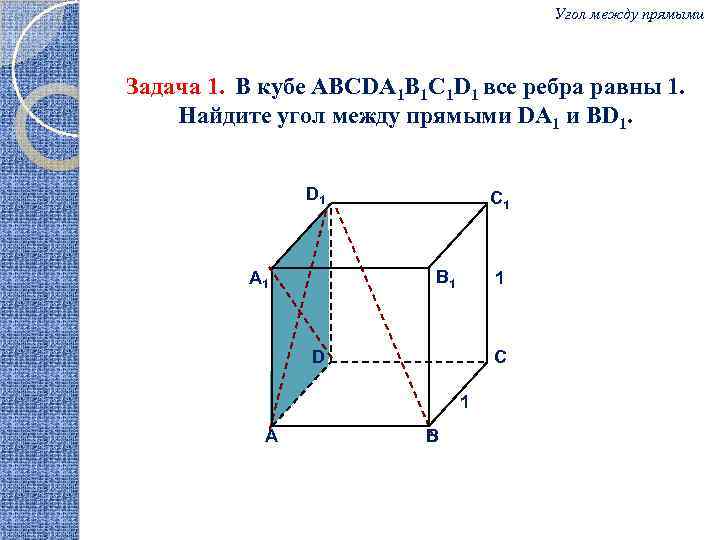
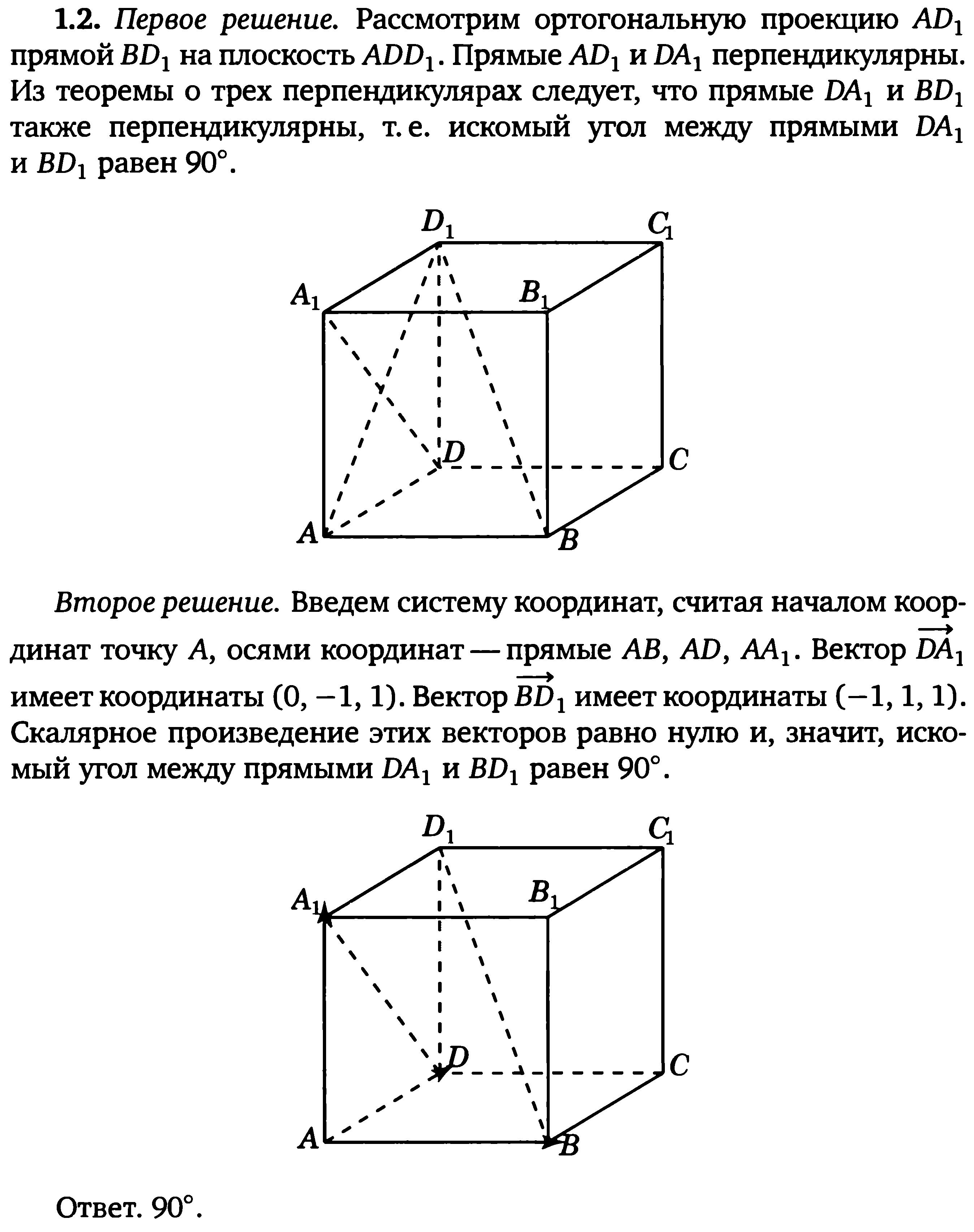
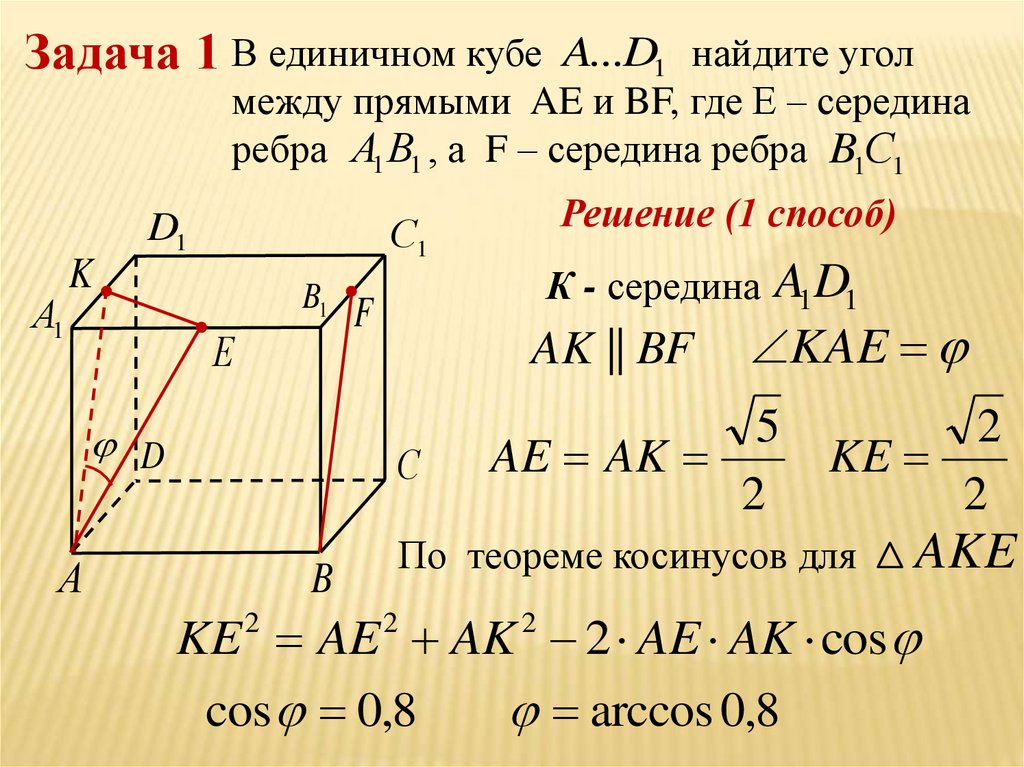
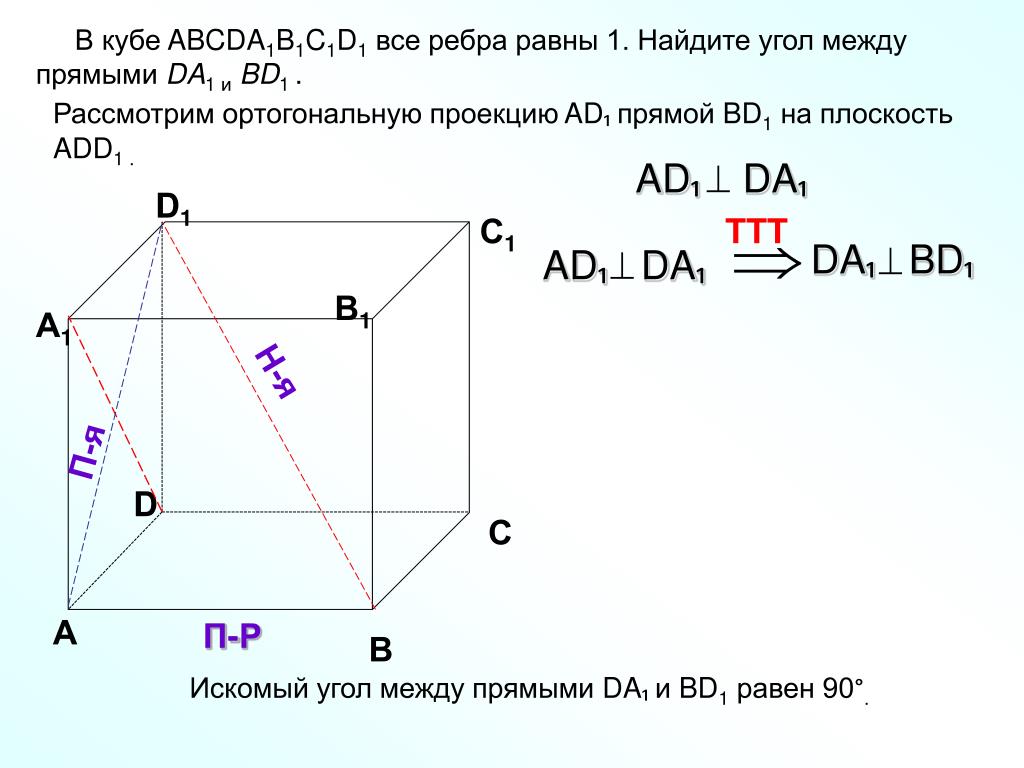
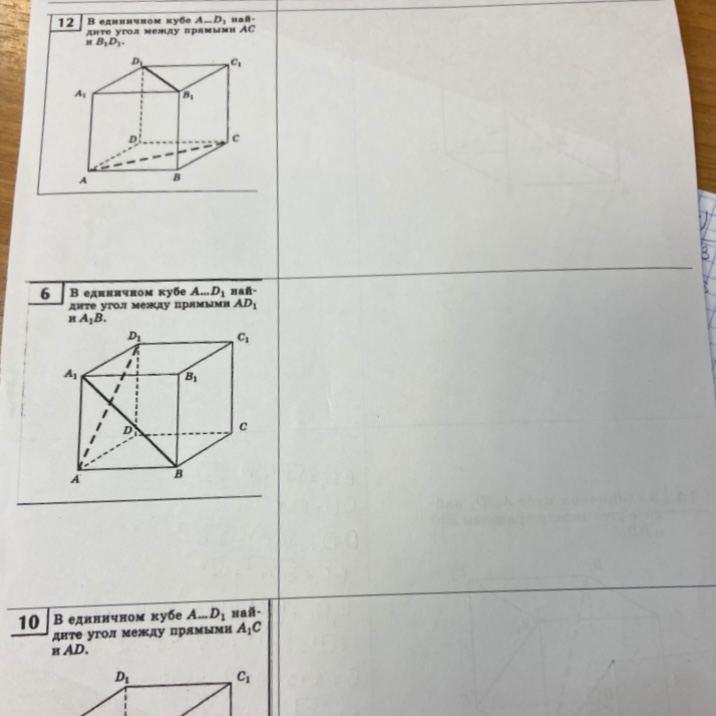
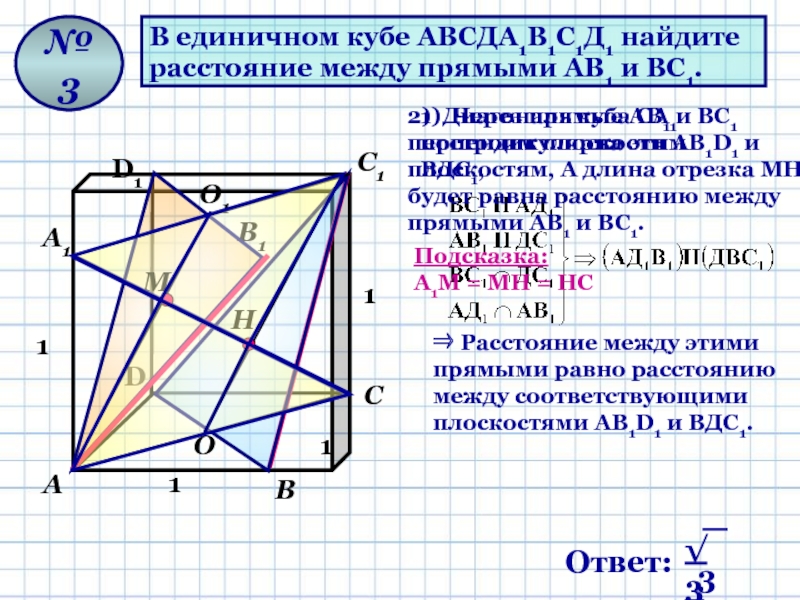
 В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми AD и CA1.
В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми AD и CA1.
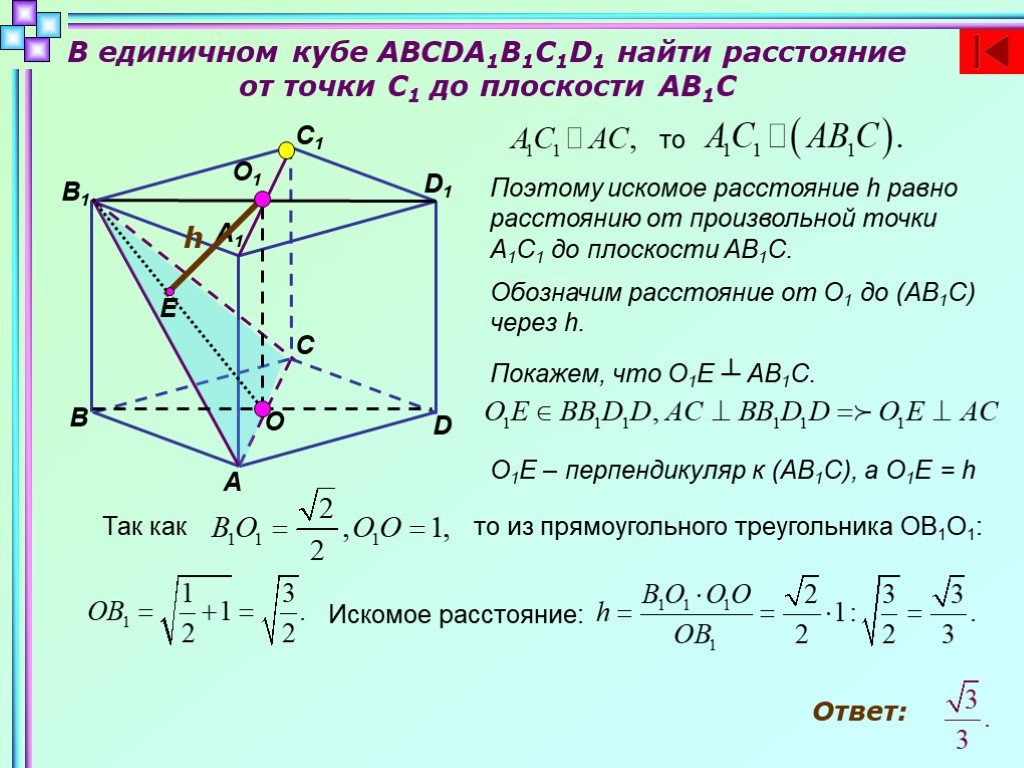
 Ответы экспертов на вопрос №4080791 в единичном кубе ABCDA1B1C1D1 найдите расстояние от вершины A до плоскости BCD1 -… - отвечают эксперты раздела …
Ответы экспертов на вопрос №4080791 в единичном кубе ABCDA1B1C1D1 найдите расстояние от вершины A до плоскости BCD1 -… - отвечают эксперты раздела …
 В кубе ABCDA1B1C1D1 все ребра равны 6. а) Докажите, что угол между прямыми AC и BC1 равен 60°. б) Найдите расстояние между прямыми AC и BC1.
В кубе ABCDA1B1C1D1 все ребра равны 6. а) Докажите, что угол между прямыми AC и BC1 равен 60°. б) Найдите расстояние между прямыми AC и BC1.
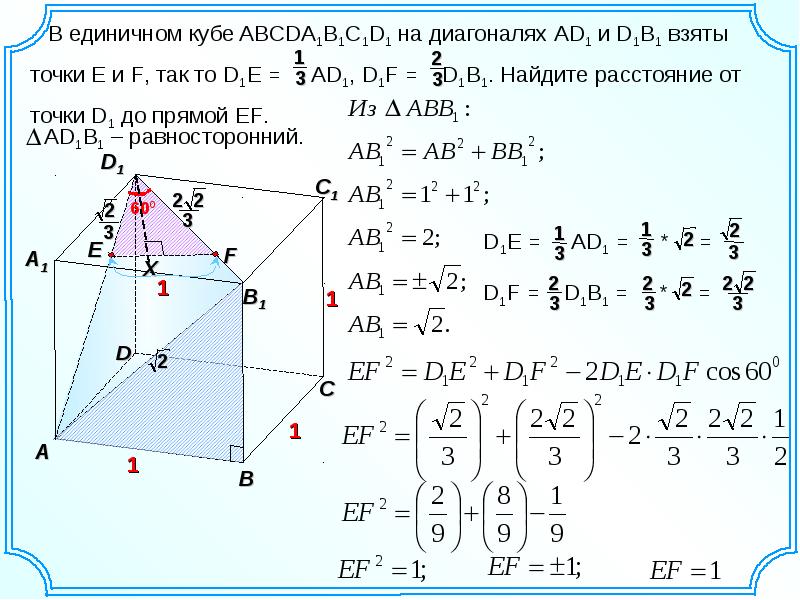
 б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA = DN:NC = 6:1.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA = DN:NC = 6:1.
 В кубе ABCDA1B1C1D1 рёбра равны 1. На продолжении отрезка A1C1 за точку C1 отмечена точка M так, что A1C1 = C1M, а на продолжении отрезка B1C за точку C отмечена точка …
В кубе ABCDA1B1C1D1 рёбра равны 1. На продолжении отрезка A1C1 за точку C1 отмечена точка M так, что A1C1 = C1M, а на продолжении отрезка B1C за точку C отмечена точка …
 Система тестов для подготовки и самоподготовки к ЕГЭ.
Система тестов для подготовки и самоподготовки к ЕГЭ.
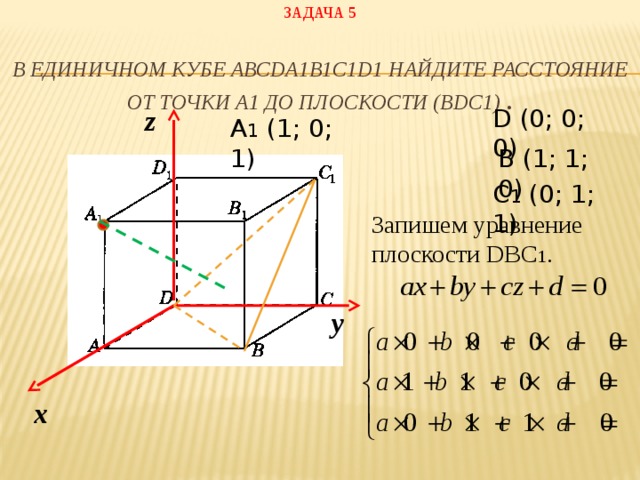
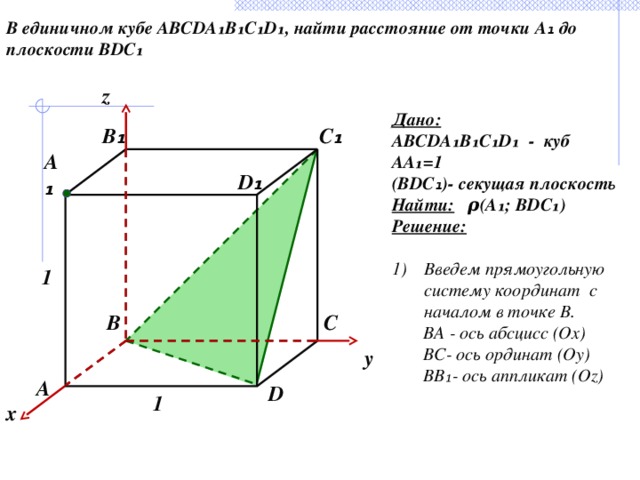
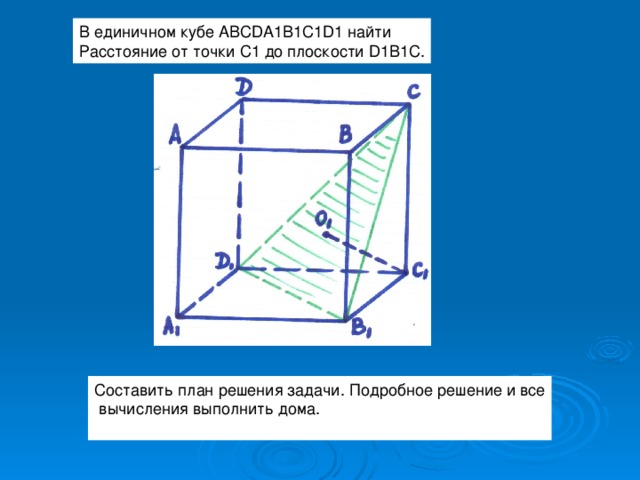 Решим задачу: в единичном кубе найдите расстояние от точки до плоскости. На этот раз давайте решим ее с помощью метода координат.
Решим задачу: в единичном кубе найдите расстояние от точки до плоскости. На этот раз давайте решим ее с помощью метода координат.
 Для решения данной задачи, нам необходимо найти расстояние от точки a до прямых bc, bd и c1d1 в единичном кубе abcda1b1c1d1.
Для решения данной задачи, нам необходимо найти расстояние от точки a до прямых bc, bd и c1d1 в единичном кубе abcda1b1c1d1.
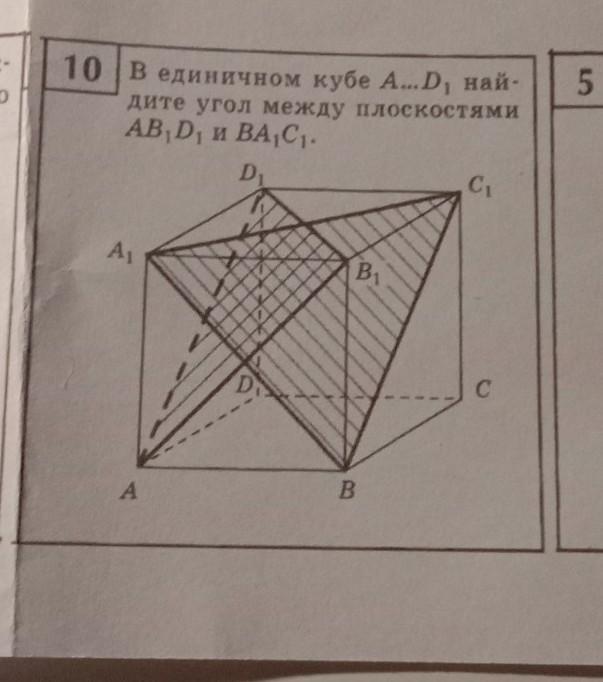
 Дан куб ABCDA1B1C1D1. а) Постройте сечение куба плоскостью, проходящей через точки В, А1 и D1. б) Найдите угол между плоскостями BA1C1 и BA1D1.
Дан куб ABCDA1B1C1D1. а) Постройте сечение куба плоскостью, проходящей через точки В, А1 и D1. б) Найдите угол между плоскостями BA1C1 и BA1D1.
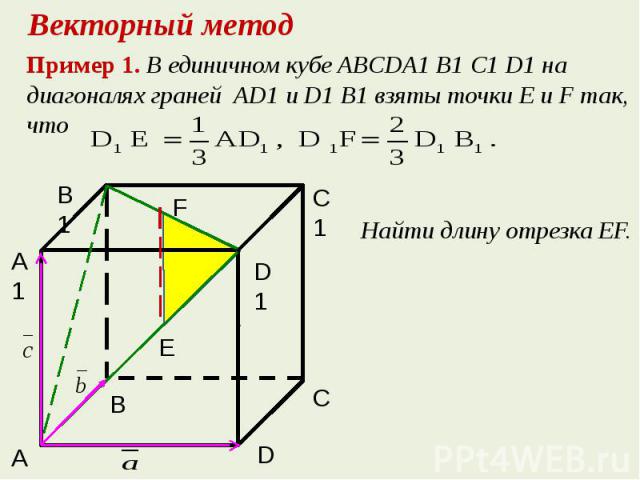 В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми AD и CA1.
В единичном кубе ABCDA1B1C1D1 найдите расстояние между прямыми AD и CA1.
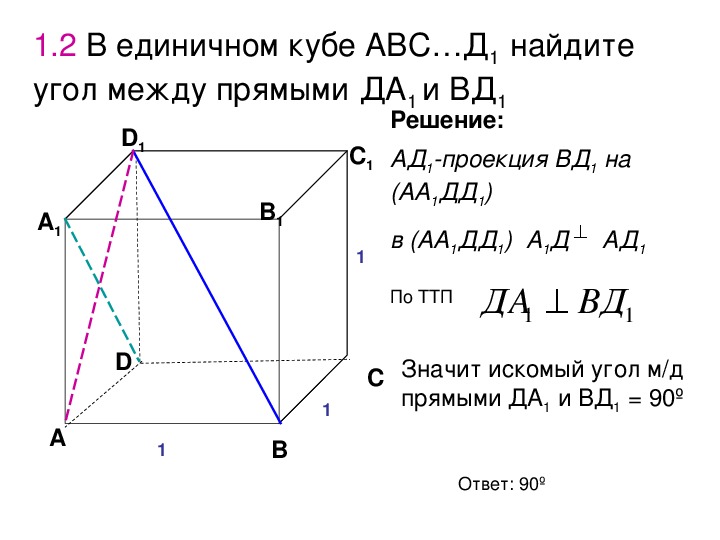 Общий приём при нахождении расстояния между двумя скрещивающимися прямыми - так на них посмотреть, чтоб одна из них превратилась в точку. То есть вдоль одной из …
Общий приём при нахождении расстояния между двумя скрещивающимися прямыми - так на них посмотреть, чтоб одна из них превратилась в точку. То есть вдоль одной из …
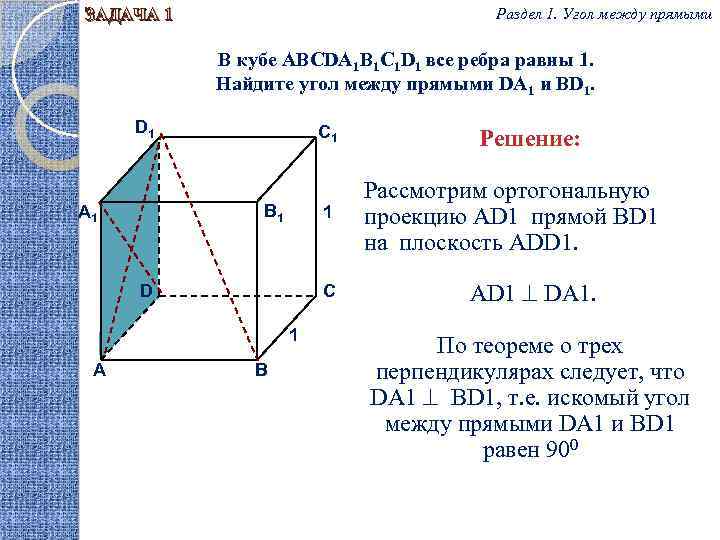
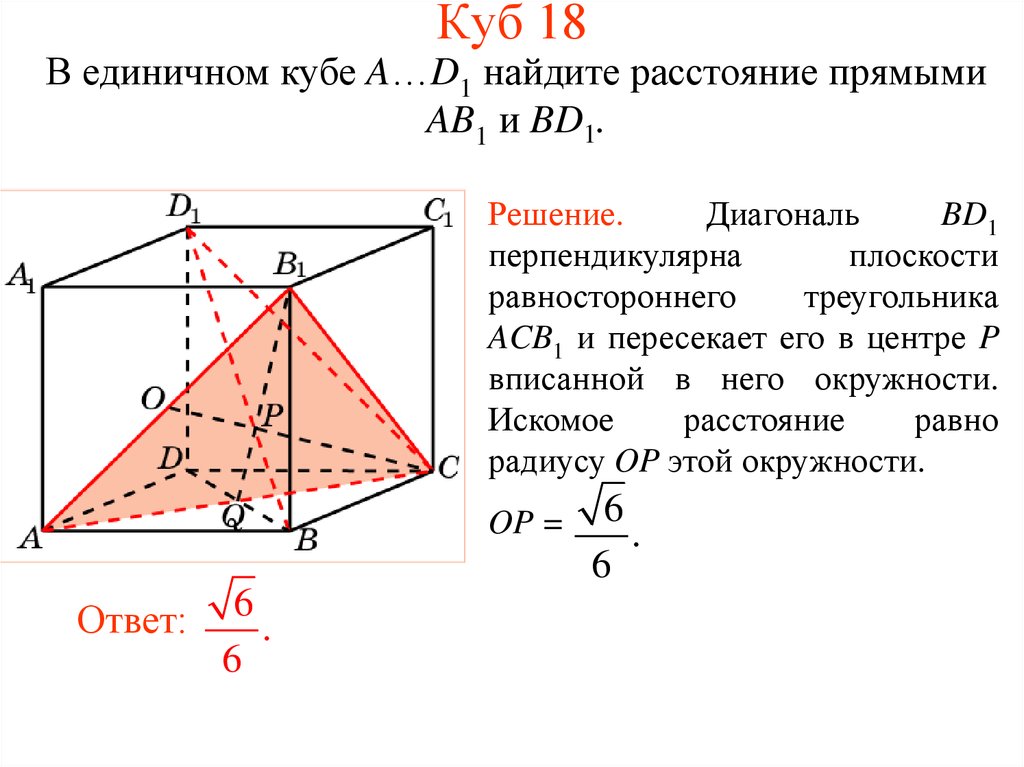
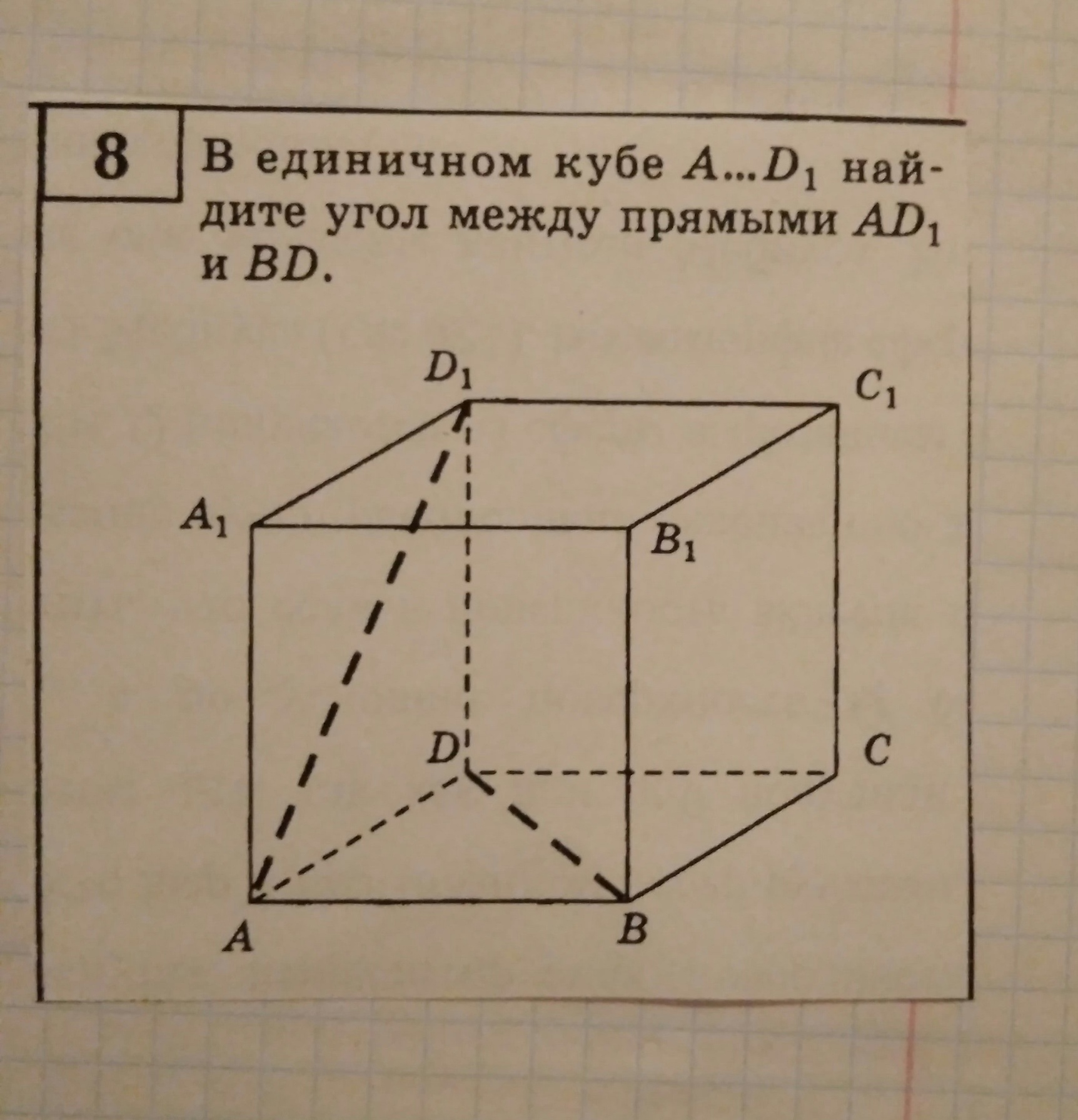
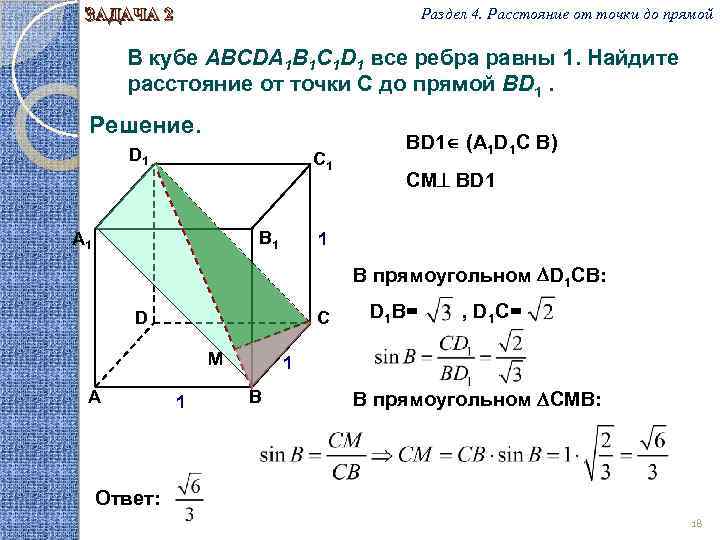 Угол между прямыми DC1 и BD – это угол в плоскости DBC1. Можно заметить, что эта плоскость определяется тремя равными отрезками BD, DC1 и BC1 – как диагонали куба. …
Угол между прямыми DC1 и BD – это угол в плоскости DBC1. Можно заметить, что эта плоскость определяется тремя равными отрезками BD, DC1 и BC1 – как диагонали куба. …
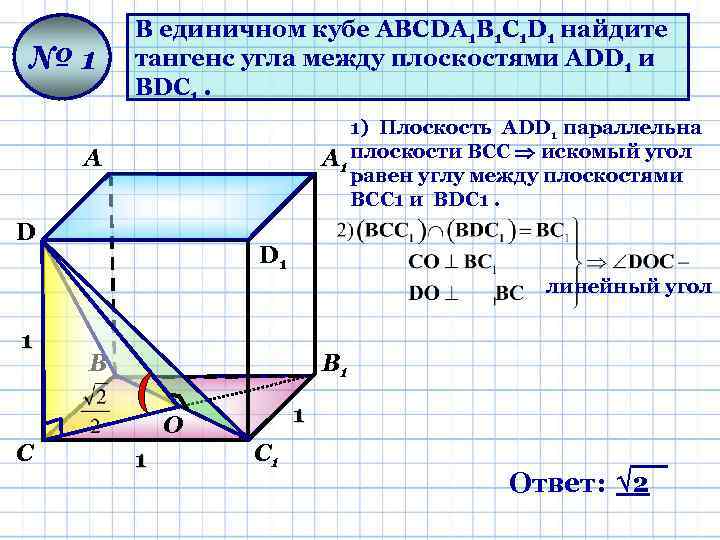
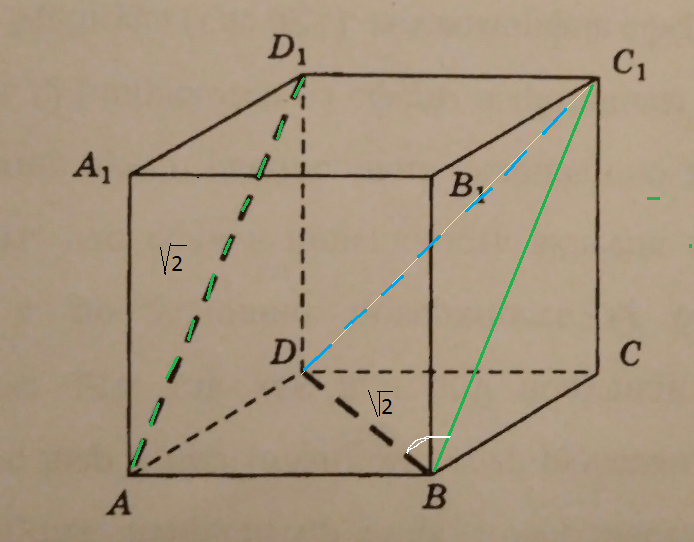 Дан куб ABCDA1B1C1D1. а) Постройте сечение куба плоскостью, проходящей через середины его рёбер АВ, B1 C1, AD. б) Найдите угол между плоскостью A1BD и …
Дан куб ABCDA1B1C1D1. а) Постройте сечение куба плоскостью, проходящей через середины его рёбер АВ, B1 C1, AD. б) Найдите угол между плоскостью A1BD и …
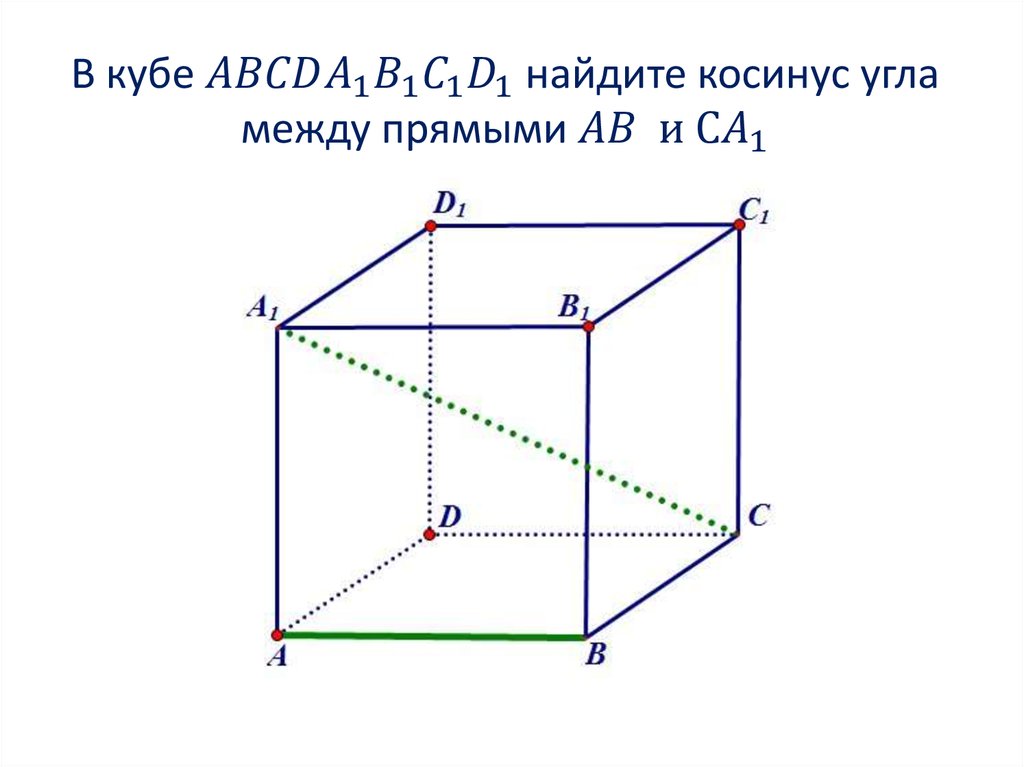 а) Пусть точка F делит ребро BB1 в отношении 1 : 2, считая от вершины B1. Докажите, что угол между прямыми BE и AC1 равен углу AC1F.
а) Пусть точка F делит ребро BB1 в отношении 1 : 2, считая от вершины B1. Докажите, что угол между прямыми BE и AC1 равен углу AC1F.
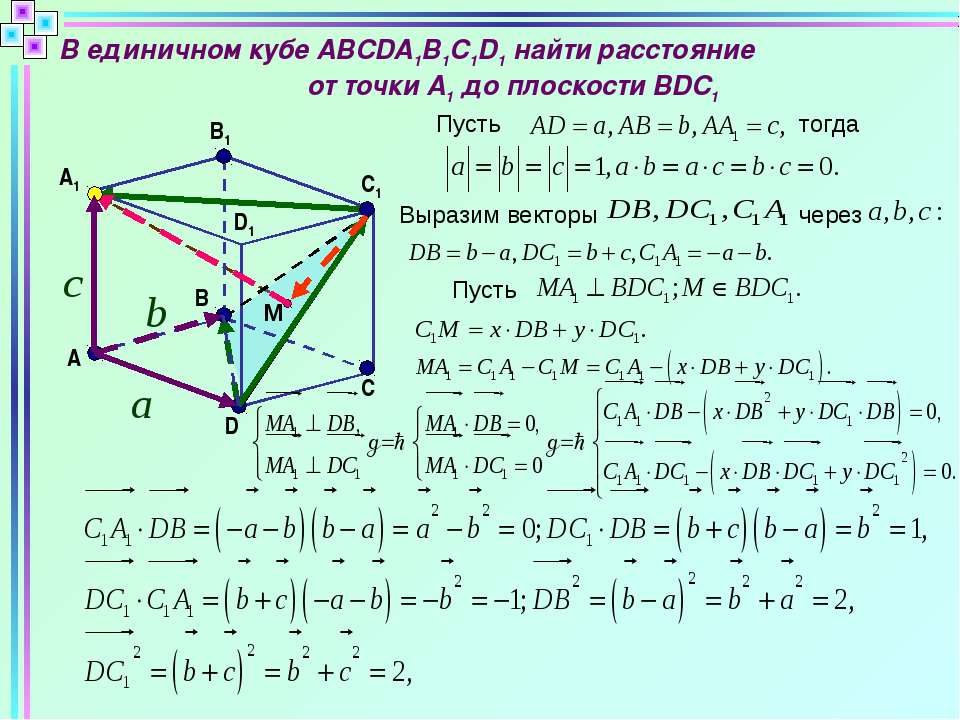
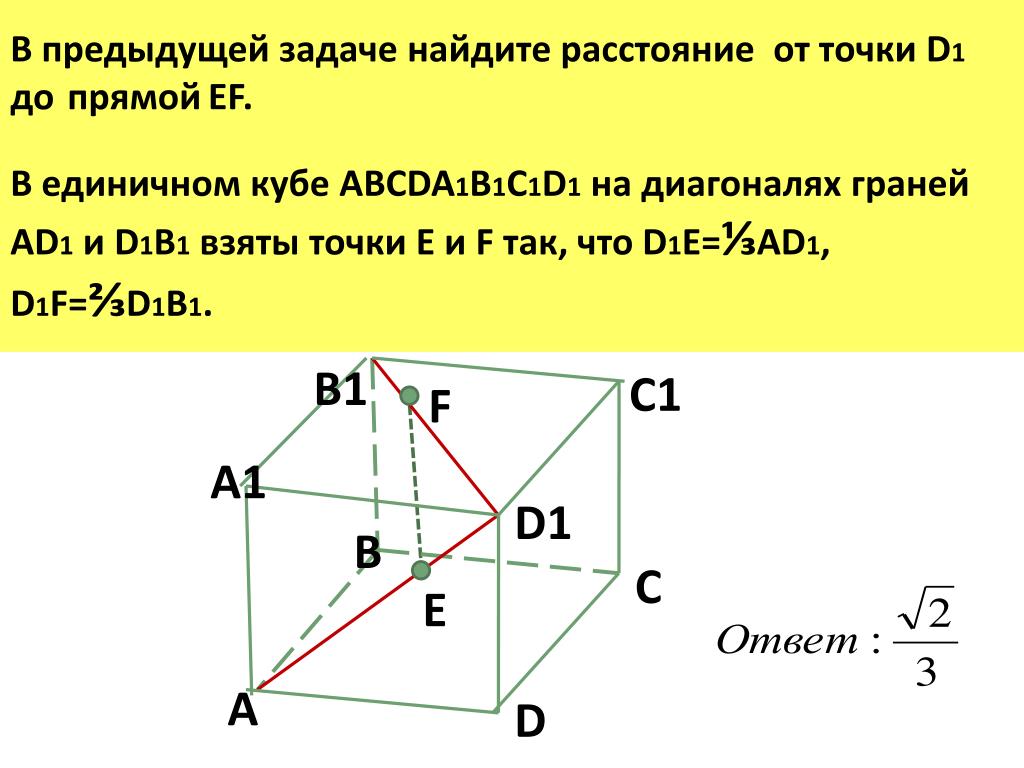
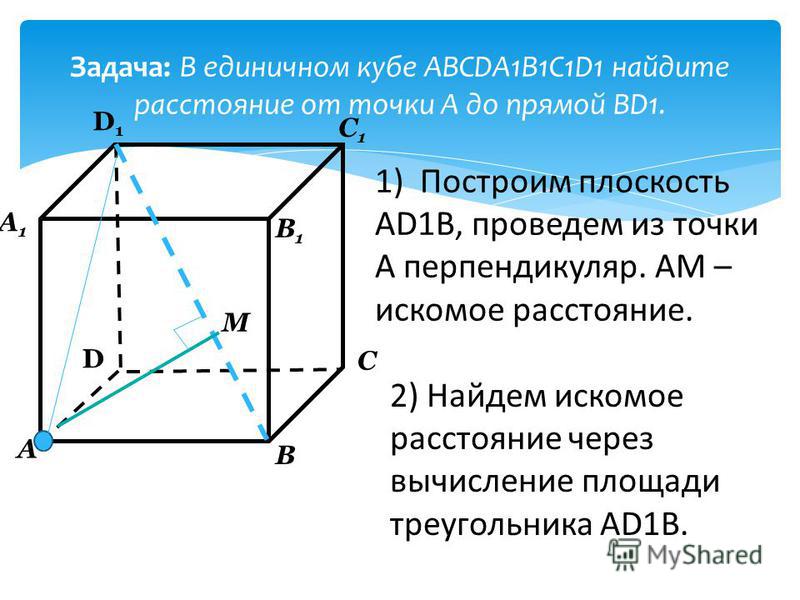 В единичном кубе ABCDA1B1C1D1 а) Опустите перпендикуляр из точки D на плоскость CAD1. б) Найдите его длину.
В единичном кубе ABCDA1B1C1D1 а) Опустите перпендикуляр из точки D на плоскость CAD1. б) Найдите его длину.
Еще по теме:





Еще по теме: