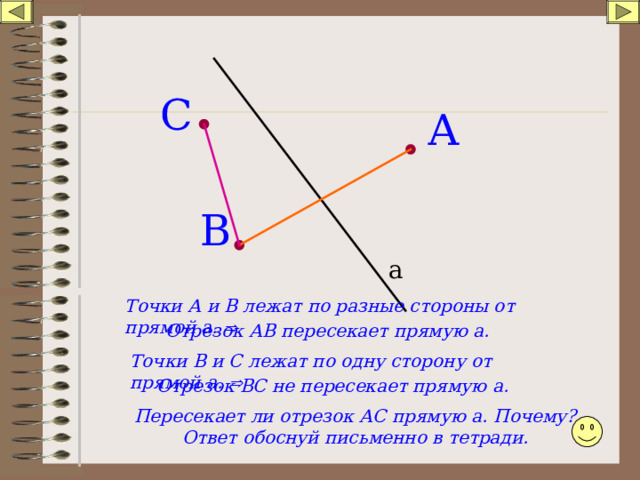
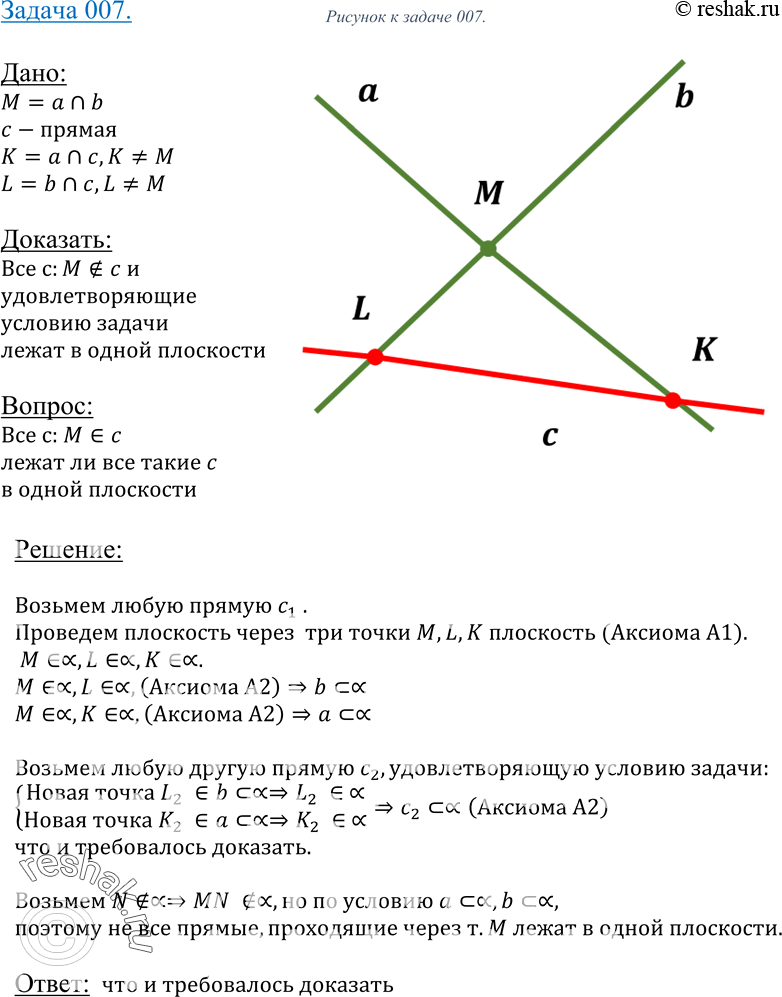
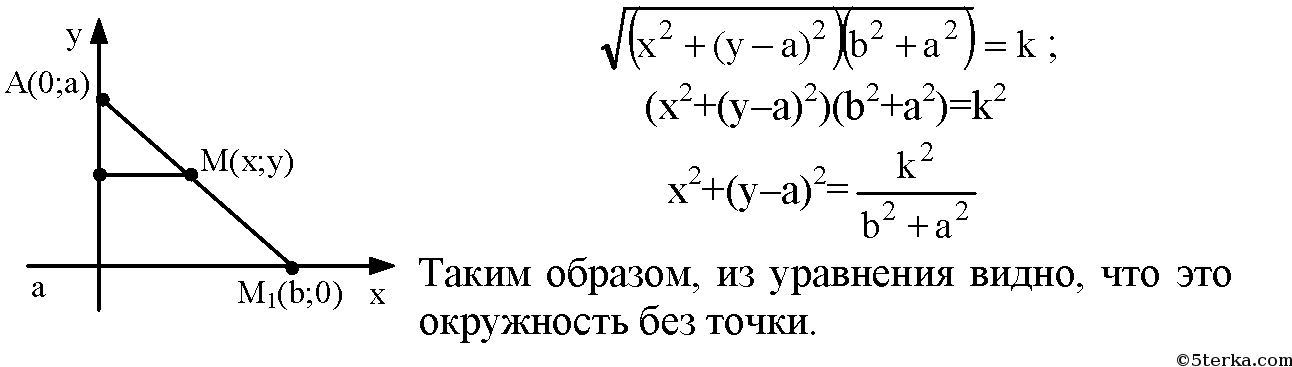Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 10 класс, Просвещение: 11 Даны прямая и точка, не лежащая на этой прямой. Докажите, что все …
ГДЗ к 11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости. (решение и ответ)
Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости. По …
Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости. Сторона …
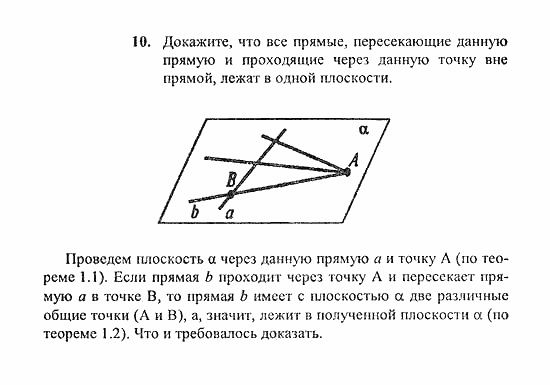Решение на Задание 11 из ГДЗ по Геометрии за 10-11 класс: Атанасян Л.С. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную …
Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Подробный ответ из решебника (ГДЗ) на Задание 8, § 4 по учебнику А. В. Погорелов. Учебник по Геометрии 7-9 класса. 2-е издание, Просвещение, 2014г.
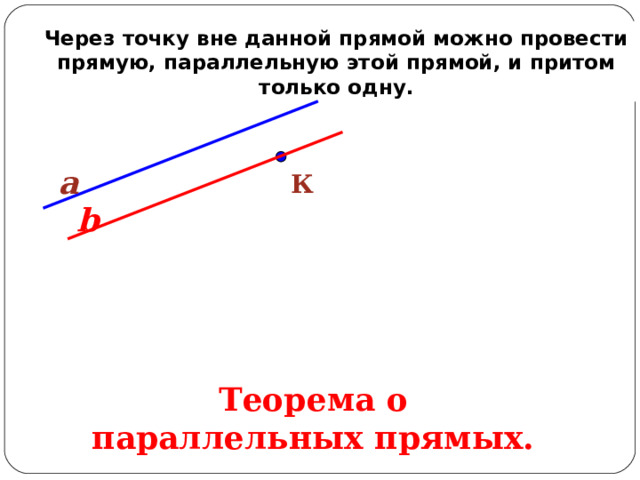
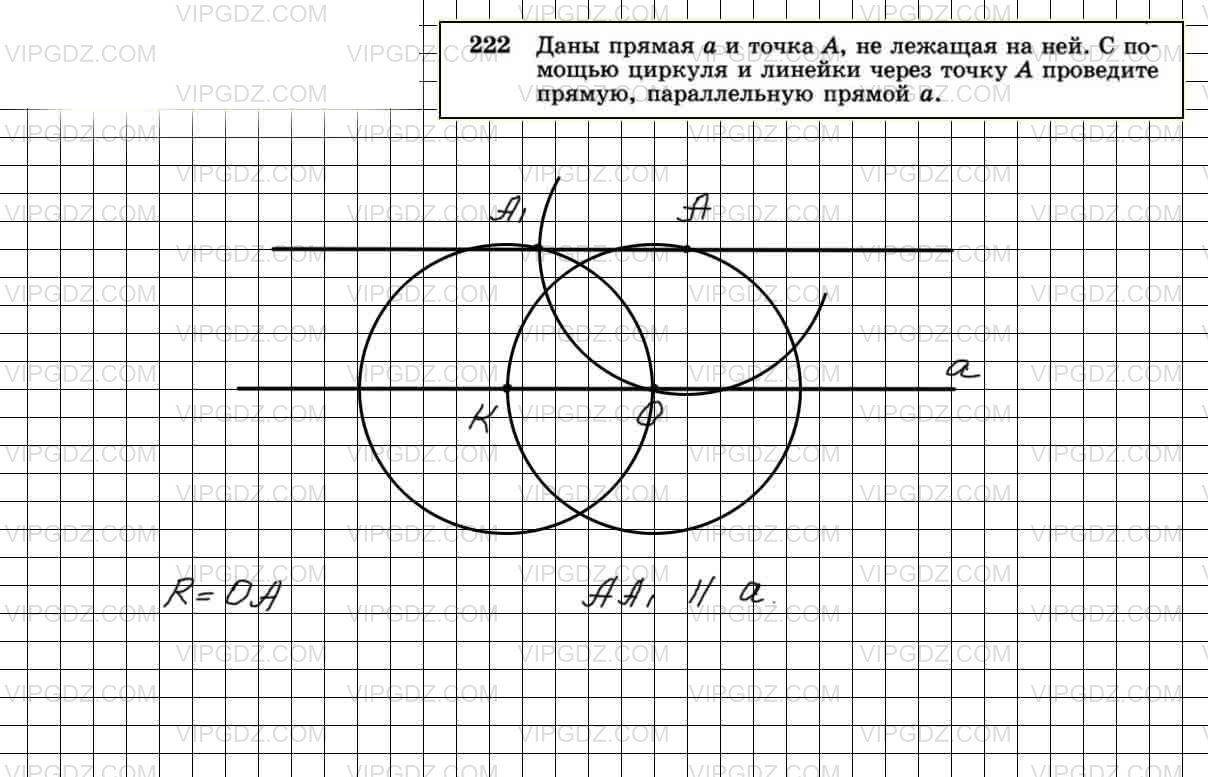
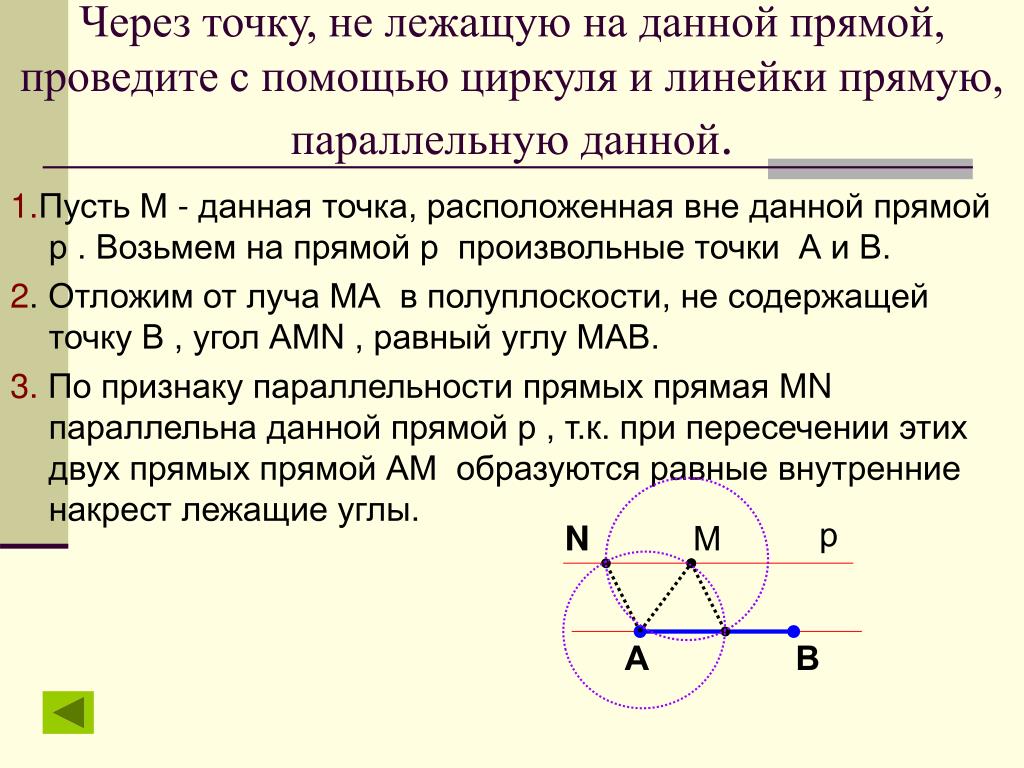
Докажите, что через точку С можно провести прямую, параллельную прямой АВ. Задача решена в п. 31 учебника (стр. 44). к главе « § 4. Сумма углов треугольника ». ← № 7. …
Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.
Нам дана прямая а и некоторая точка М, которая не лежит на этой прямой. Нам нужно доказать, что все прямые, которые проходят через точку М и пересекают прямую а …
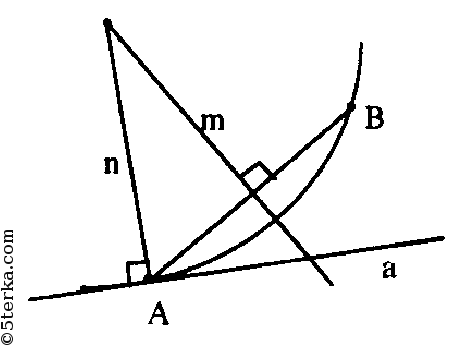
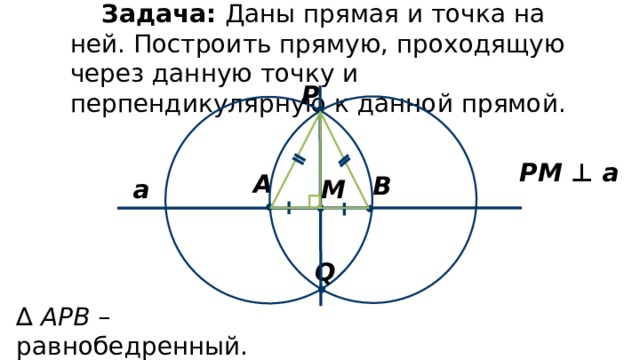
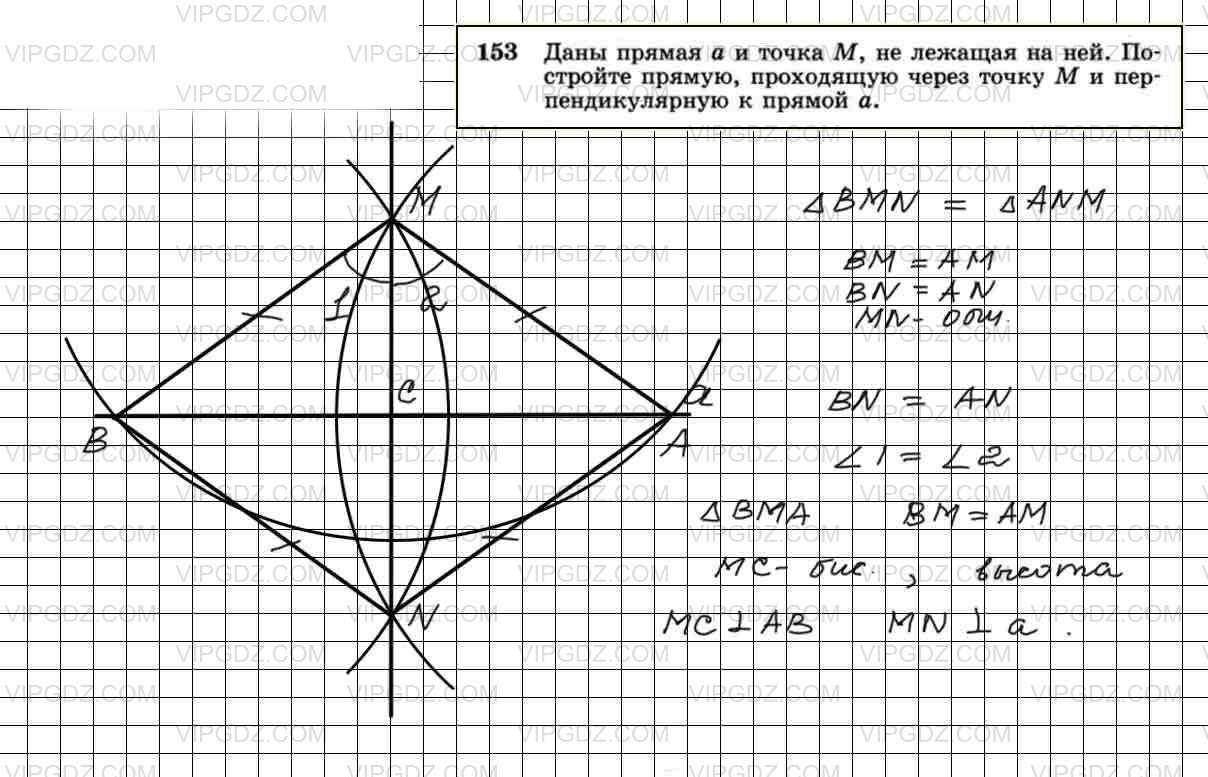
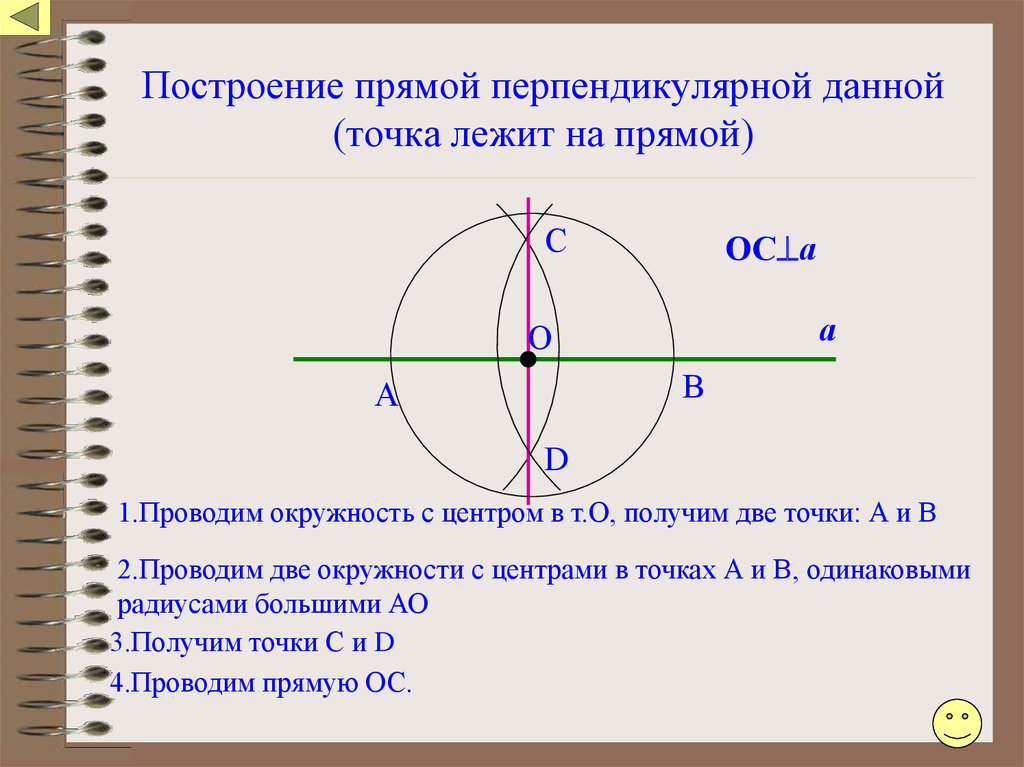
Построить прямую проходящую через данную точку и перпендикулярную к данной прямой. Дано: прямая m, Mm. Построить:МNm. Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на …
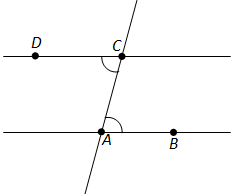
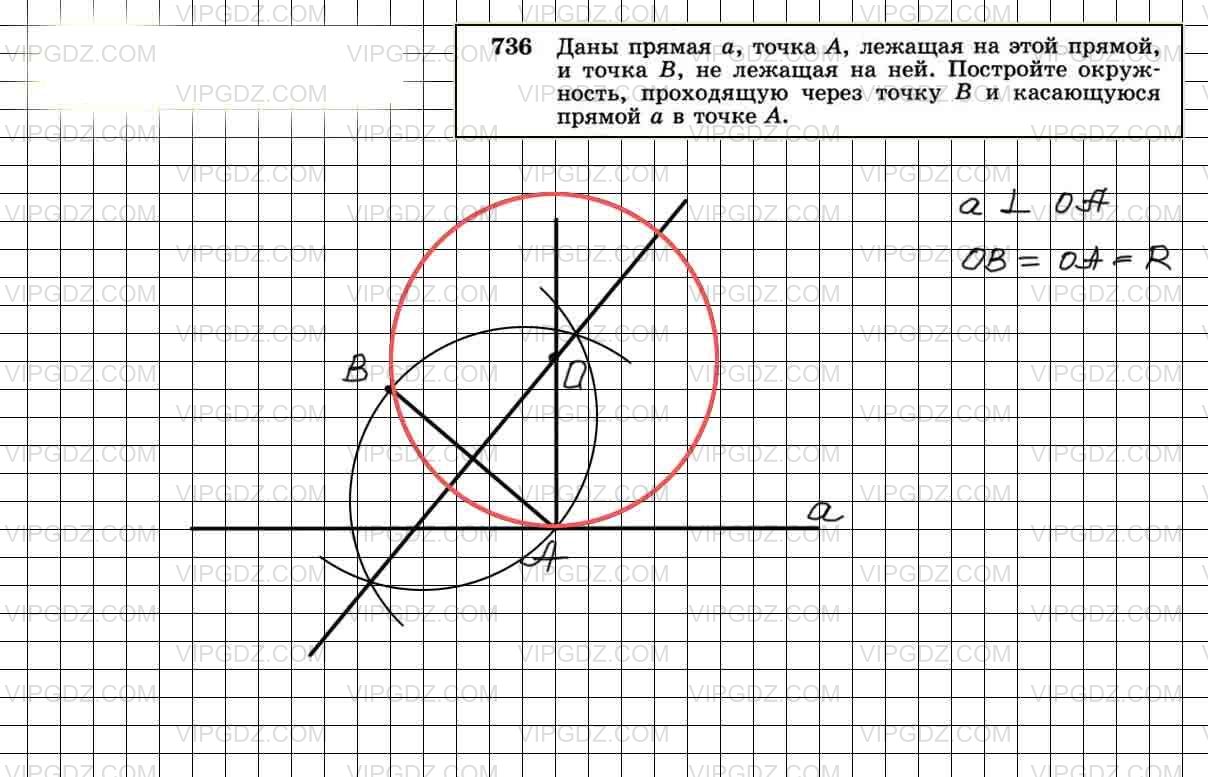
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 8 класс, Просвещение: Даны прямая а, точка А, лежащая на этой прямой, и точка В, не лежащая …
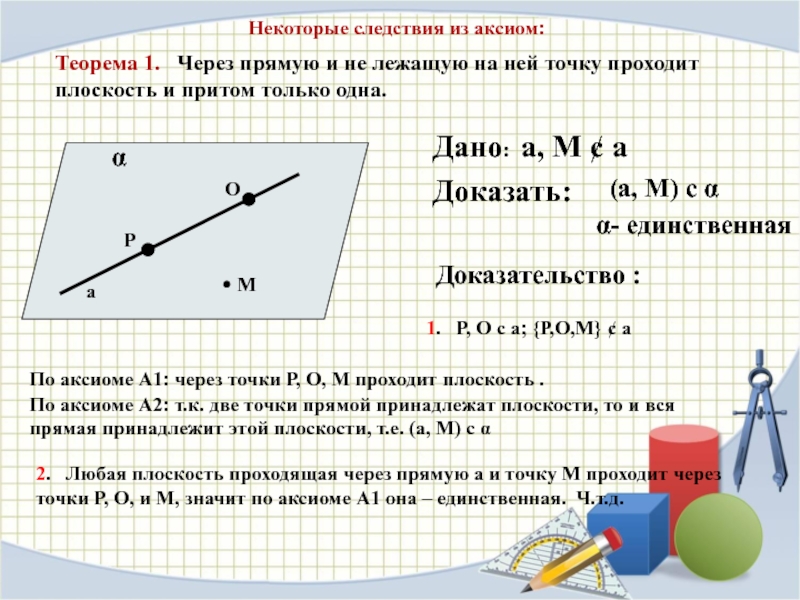
Рассмотрим точки A и B, лежащие на прямой a. Точки A,B и C не лежат на одной прямой а значит, существует единственная плоскость α, проходящая через эти точки.
Если через точку а проходят 3 прямые, то только одна из них может быть параллельна заданной. Две другие точно нет. Если они не параллельны, то они пересекутся с …
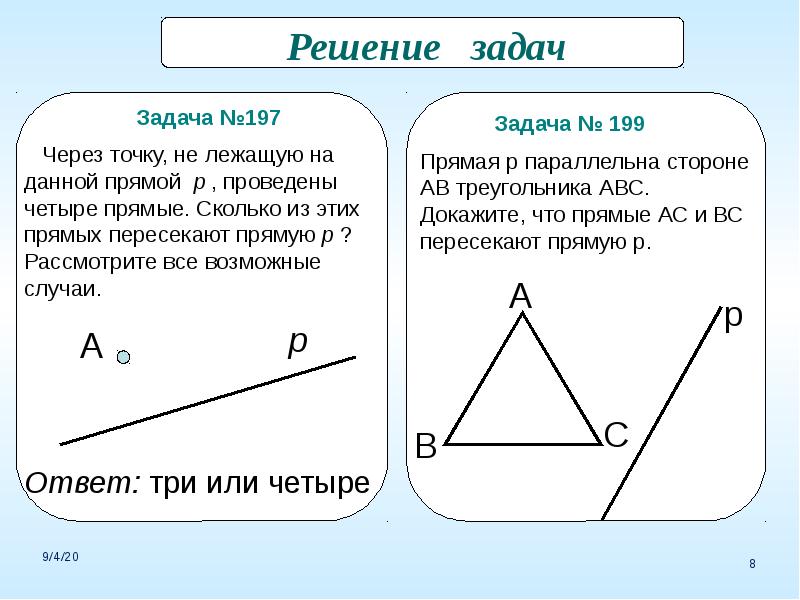
Даны прямая k и точка P, не лежащая на этой прямой. Через точку P провели 4 различные прямые. Сколько из них точно будут пересекать прямую k?
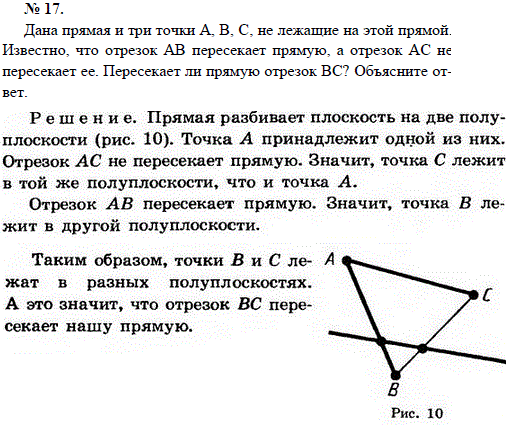
Проведем через точки А и С прямую (аксиома 1). Прямые АВ и АС различны, так как точка С не лежит на прямой АВ. Проведем через прямые АВ и АС плоскость с (аксиома 3).
Еще по теме:
Еще по теме:
