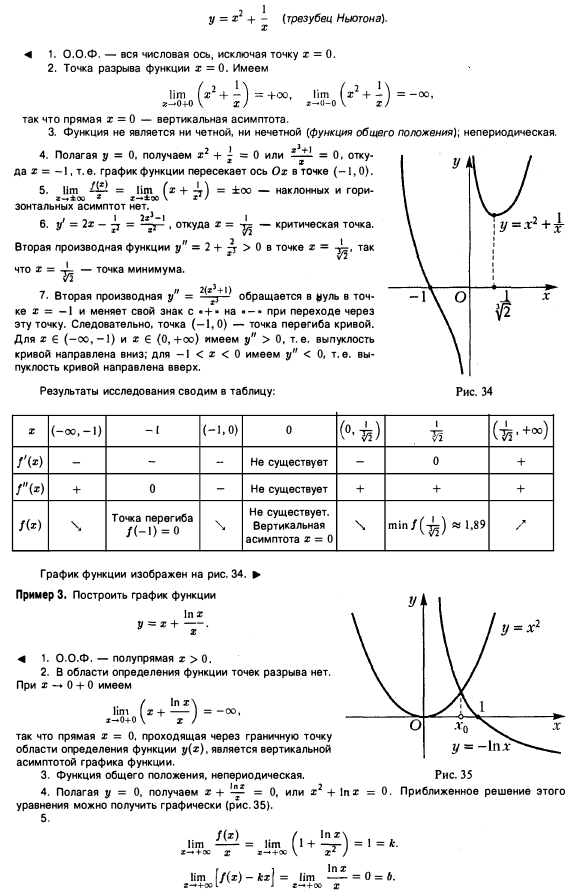
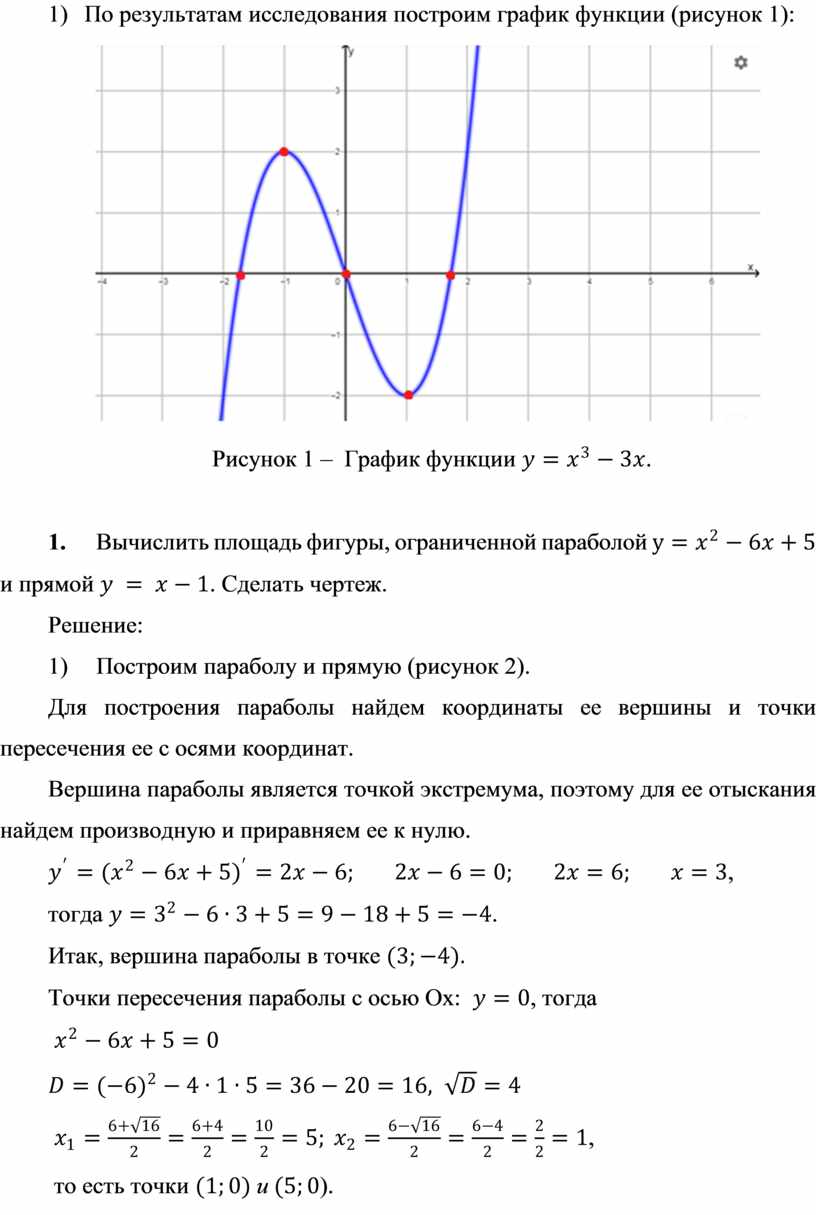
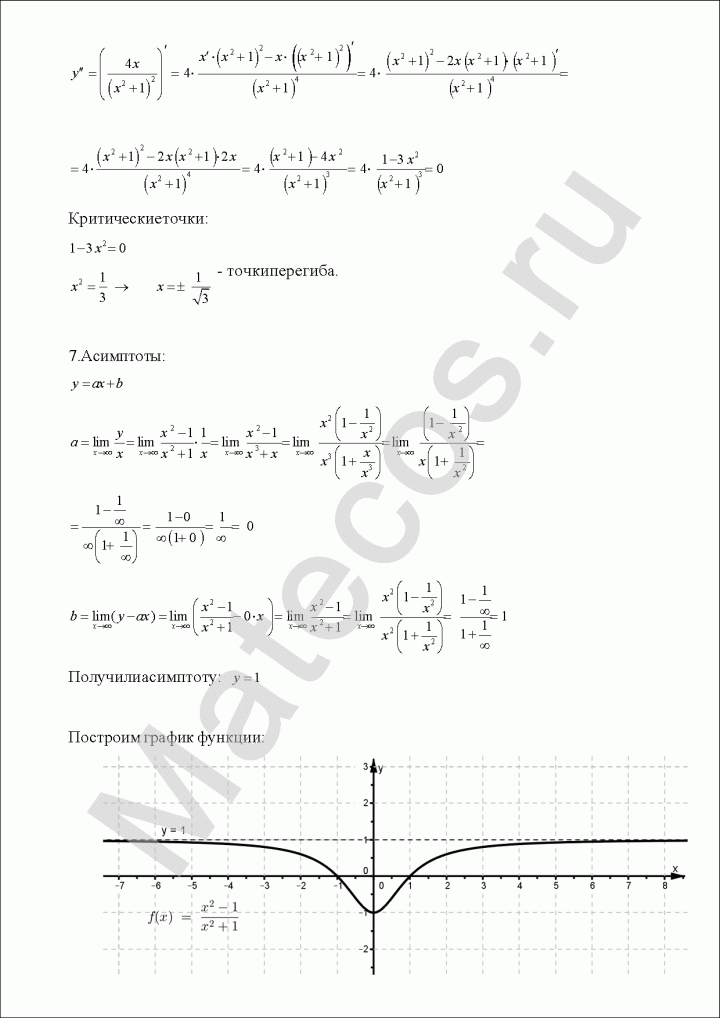
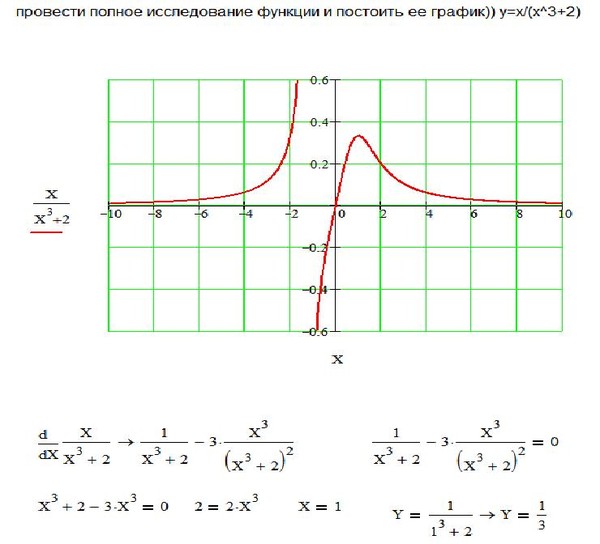
Пример 5. Провести полное исследование функции и построить её график. Решение: понеслась нелёгкая: 1) Функция определена и непрерывна на всей числовой прямой: .
В данном разделе представлены бесплатные готовые примеры на тему «Исследование функции и построение графика» для функций различного типа: многочлен, дробно …
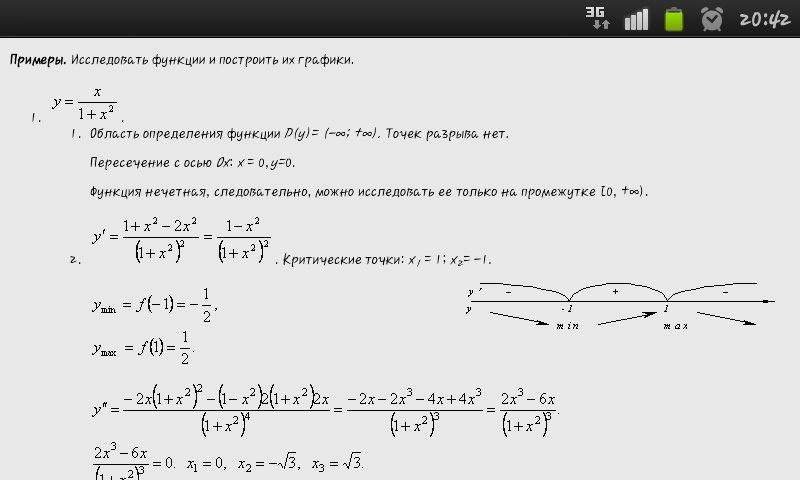Чтобы исследовать функцию и построить ее график необходимо: 1) найти область определения функции, то есть множество всех точек для которых существует значение …
Для того, чтобы построить график функции необходимо провести полное исследование заданной функции. Затем поэтапно, используя полученные результаты, построить график. Как построить график функции? После …
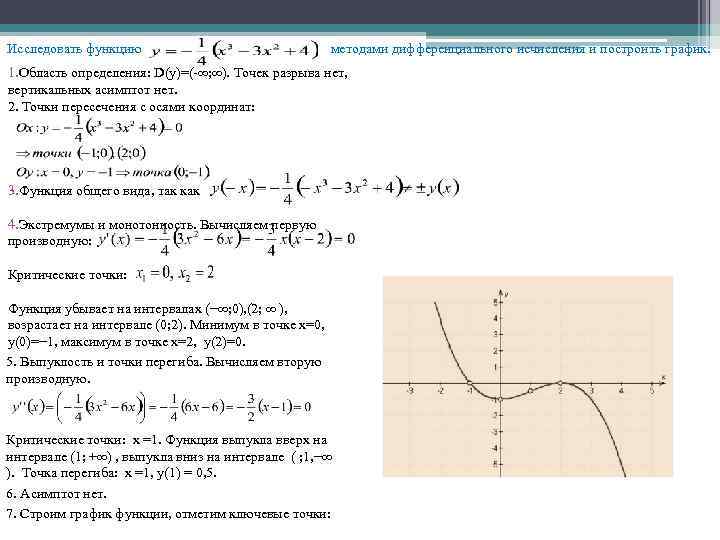Пример №1. Провести полное исследование функции и построить ее график. 1) Функция определена всюду, кроме точек . 2) Функция нечетная, так как f (-x) = -f (x), и, следовательно, ее график симметричен …
Построить график функции. Построить асимптоты. Отметить важные точки на графике. Используйте этот алгоритм для решения своих заданий на исследование функций, и вы …
Экстремумы функции: интервалы (отрезки) возрастания и убывания функции, а также локальные (или относительные) и глобальные (или абсолютные) минимумы и …
Чтобы построить верный график функции, необходимо сначала провести ее исследование. Основные этапы: Определение области существования функции. Проверка на четность и нечетность. …
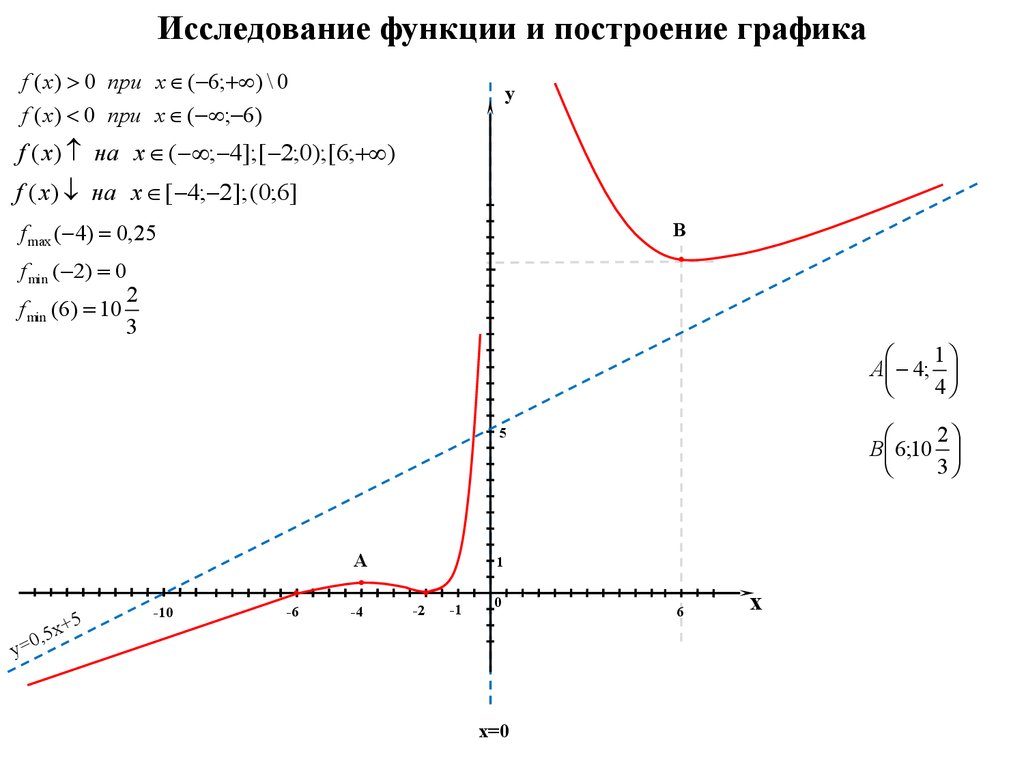
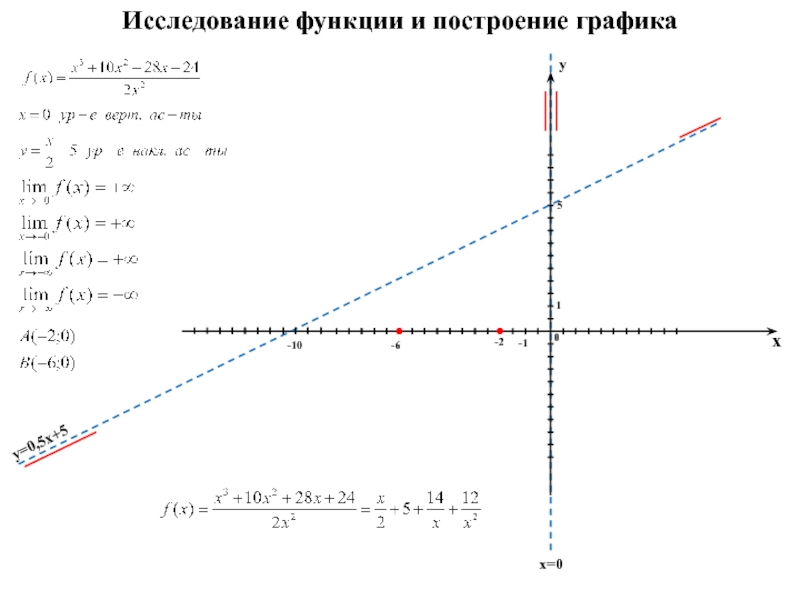
Пример 1 Исследовать функцию и построить ее график. Решение: А) область определения ; функция непрерывна в области определения; – точка разрыва, т.к. ; . Тогда – …
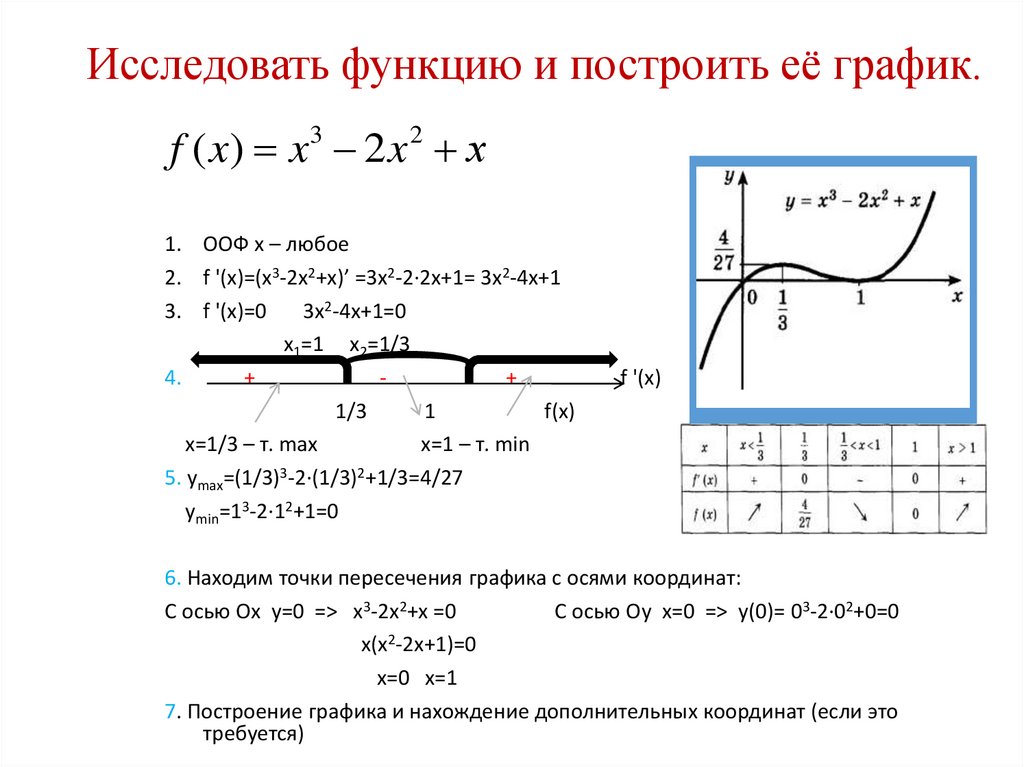
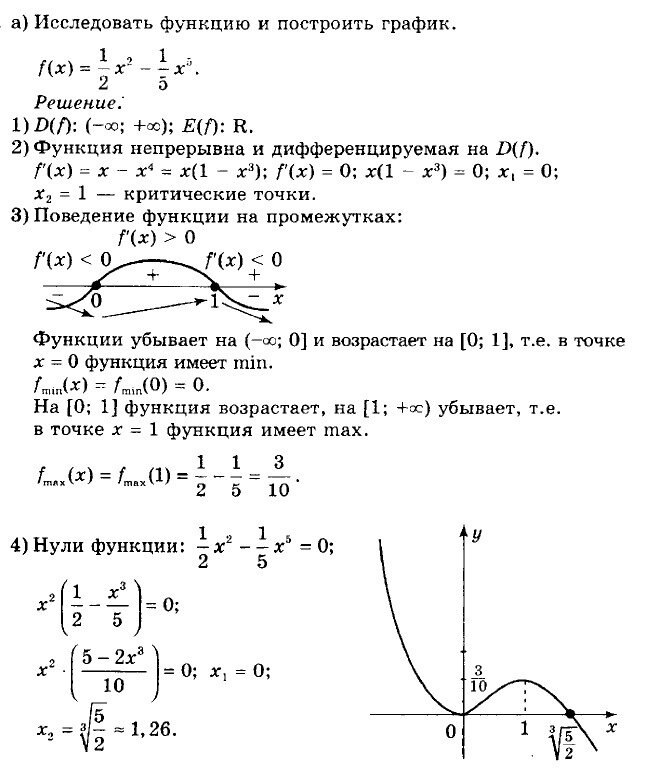Пример 1: Исследовать функцию и построить ее график. Решение от преподавателя: 1) Область определения функции х – любое. 2) Четность или нечетность функции. y (-x) = y (x), четная функция. 3) Точки …
1. Найти область определения функции, классифицировать точки разрыва. 2. Исследовать функцию на четность и периодичность. 3. Провести анализ асимптотического поведения …
**Производная функции** Для нахождения экстремумов и анализа поведения (возрастание/убывание), необходимо вычислить первую производную функции.
Здесь нам нужно провести исследование функции \( y = \frac{-2x^4}{(x+2)^3} \) и построить ее график. Исследование функции включает в себя несколько этапов, таких как …
план полного исследования функции, приводящий к построению графика. В части 2 рассмотрены шесть разнообразных примеров, иллюстрирующие сформулированные в …
.files/image216.jpg)
Подробнейшее описание алгоритма в теории, как выполнить полное исследование функции с помощью производной. 8 пунктов в исследовании функции - …
Нахождение дополнительных точек и построение графика В большинстве примеров для самоконтроля и более точного построения графика нужно найти дополнительные точки.
Еще по теме:
Еще по теме:
