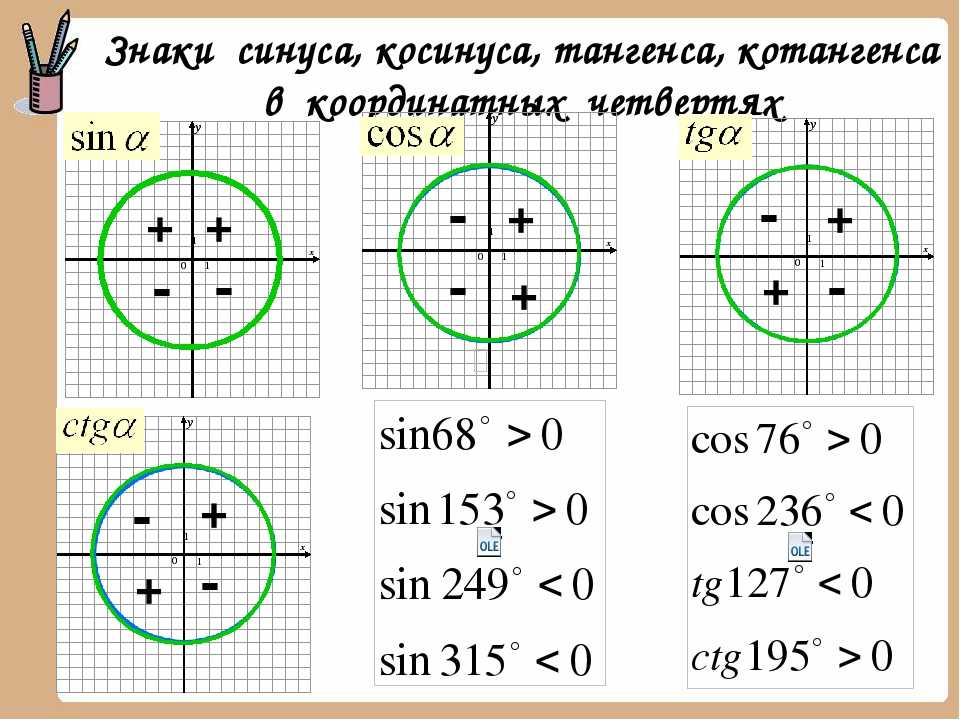
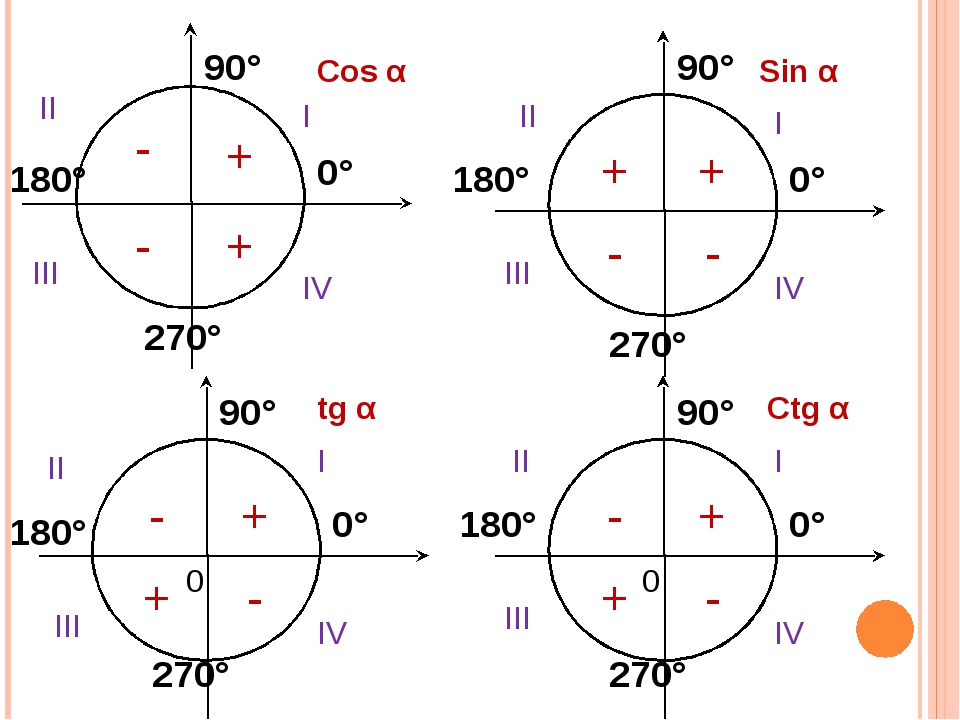
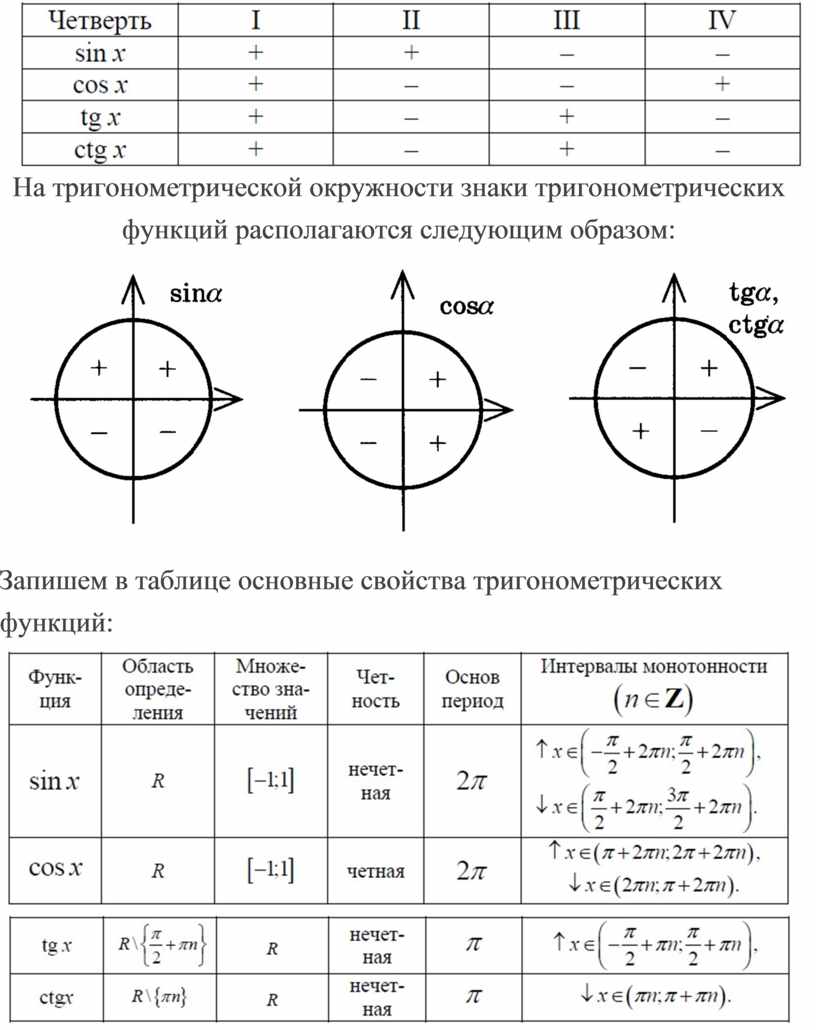
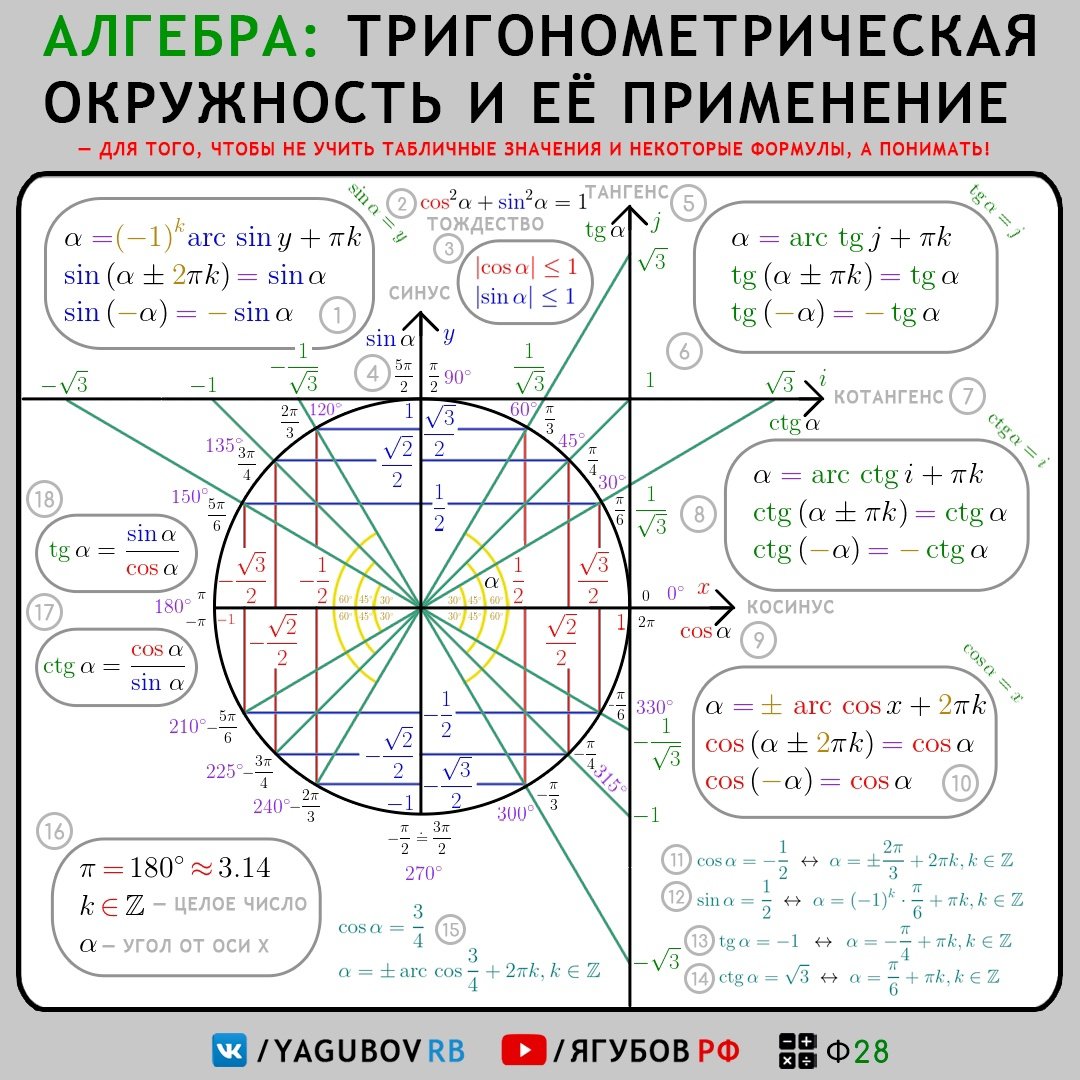
 Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано!
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано!
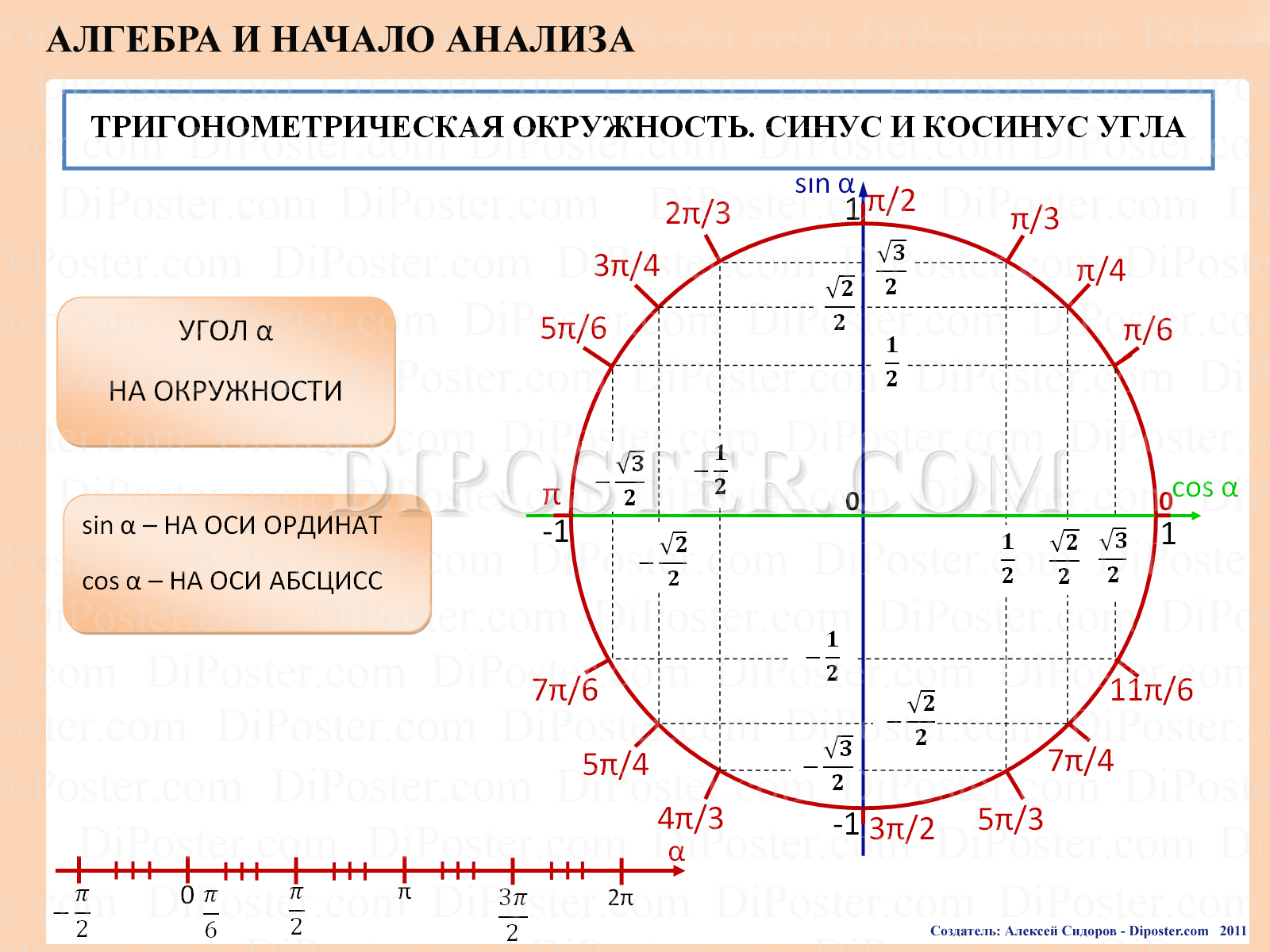
 Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Тригонометрический круг заменяет десяток таблиц.
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое. Тригонометрический круг заменяет десяток таблиц.
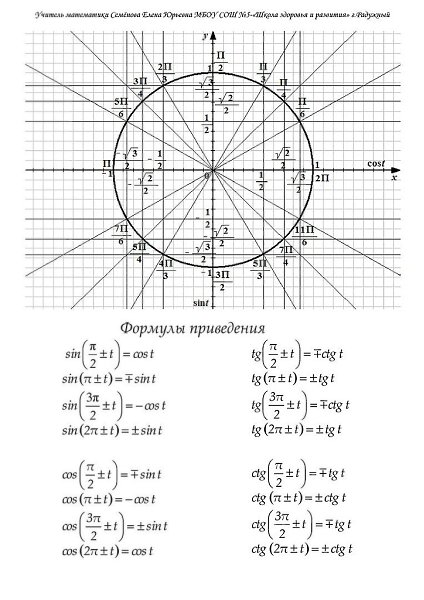
 Тригонометрия в прямоугольном треугольнике: синус, косинус, тангенс, котангенс. Тригонометрический круг. Таблица значений. Формулы приведения.
Тригонометрия в прямоугольном треугольнике: синус, косинус, тангенс, котангенс. Тригонометрический круг. Таблица значений. Формулы приведения.
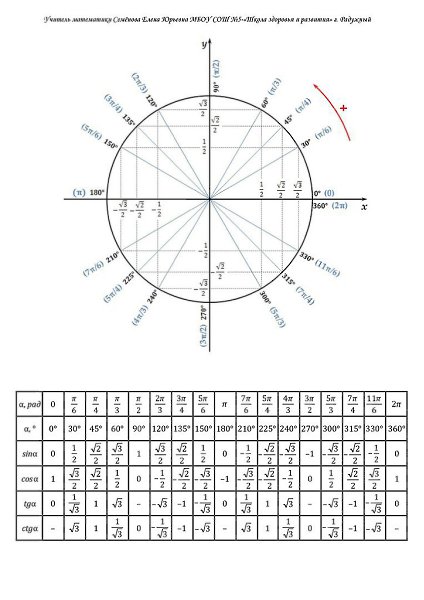
 Таблица для тригонометрического круга. 24 июня, 2021. . Тригонометрический круг со всеми значениями — как пользоваться и вычислять …
Таблица для тригонометрического круга. 24 июня, 2021. . Тригонометрический круг со всеми значениями — как пользоваться и вычислять …
 Единичная окружность или интерактивный тригонометрический круг поможет увидеть, что такое тригонометрические функции синус, косинус, тангенс, котангенс, секанс, косеканс. …
Единичная окружность или интерактивный тригонометрический круг поможет увидеть, что такое тригонометрические функции синус, косинус, тангенс, котангенс, секанс, косеканс. …
 Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы?
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы?
 Тригонометрическая таблица круг — это таблица, которая содержит значения тригонометрических функций (синуса, косинуса, тангенса, котангенса, секанса и …
Тригонометрическая таблица круг — это таблица, которая содержит значения тригонометрических функций (синуса, косинуса, тангенса, котангенса, секанса и …
 Тригонометрический круг. Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, …
Тригонометрический круг. Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, …
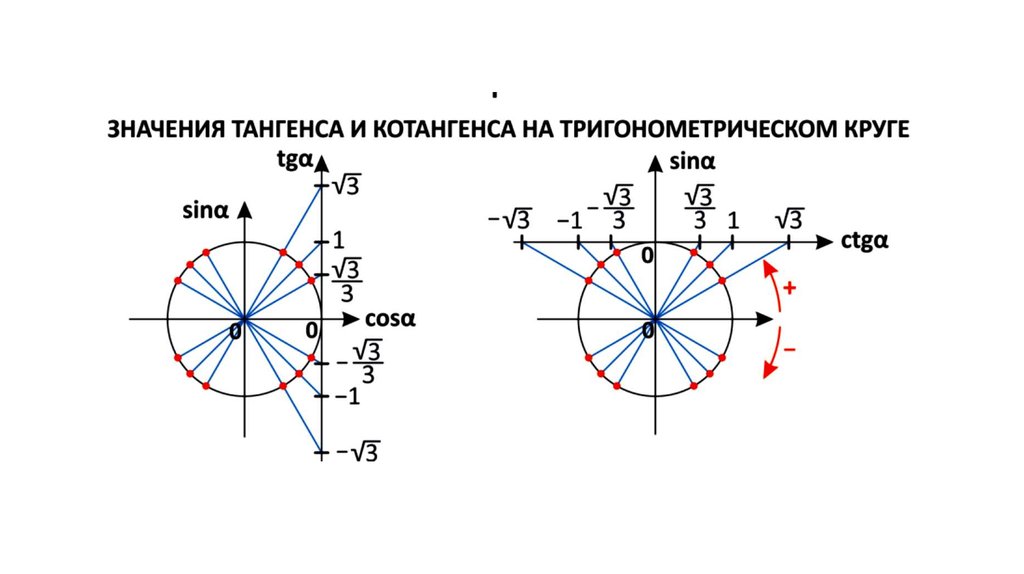
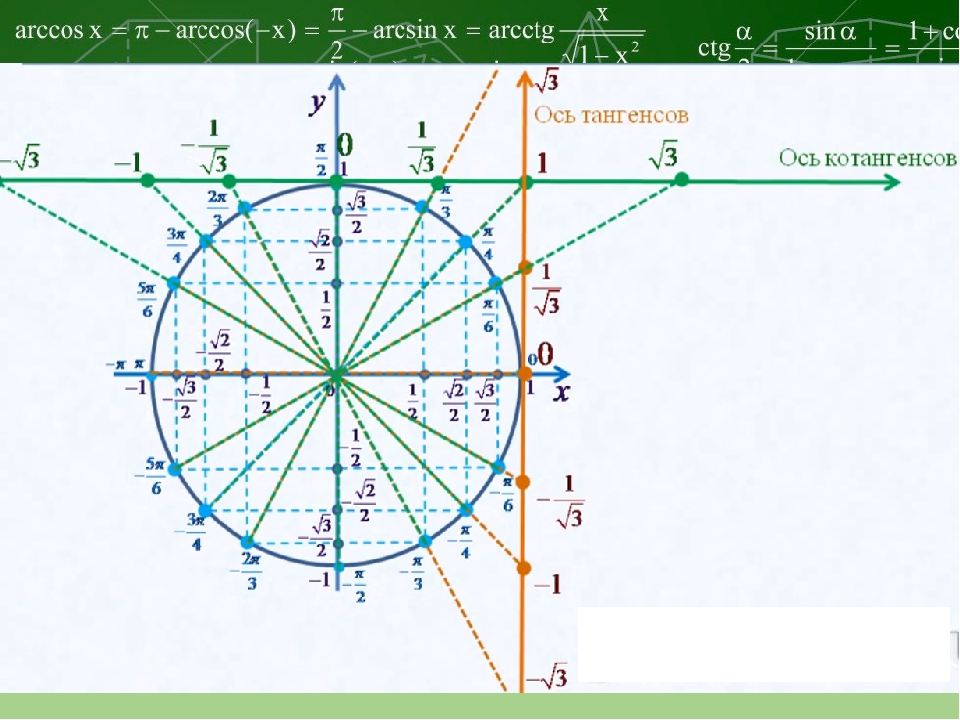
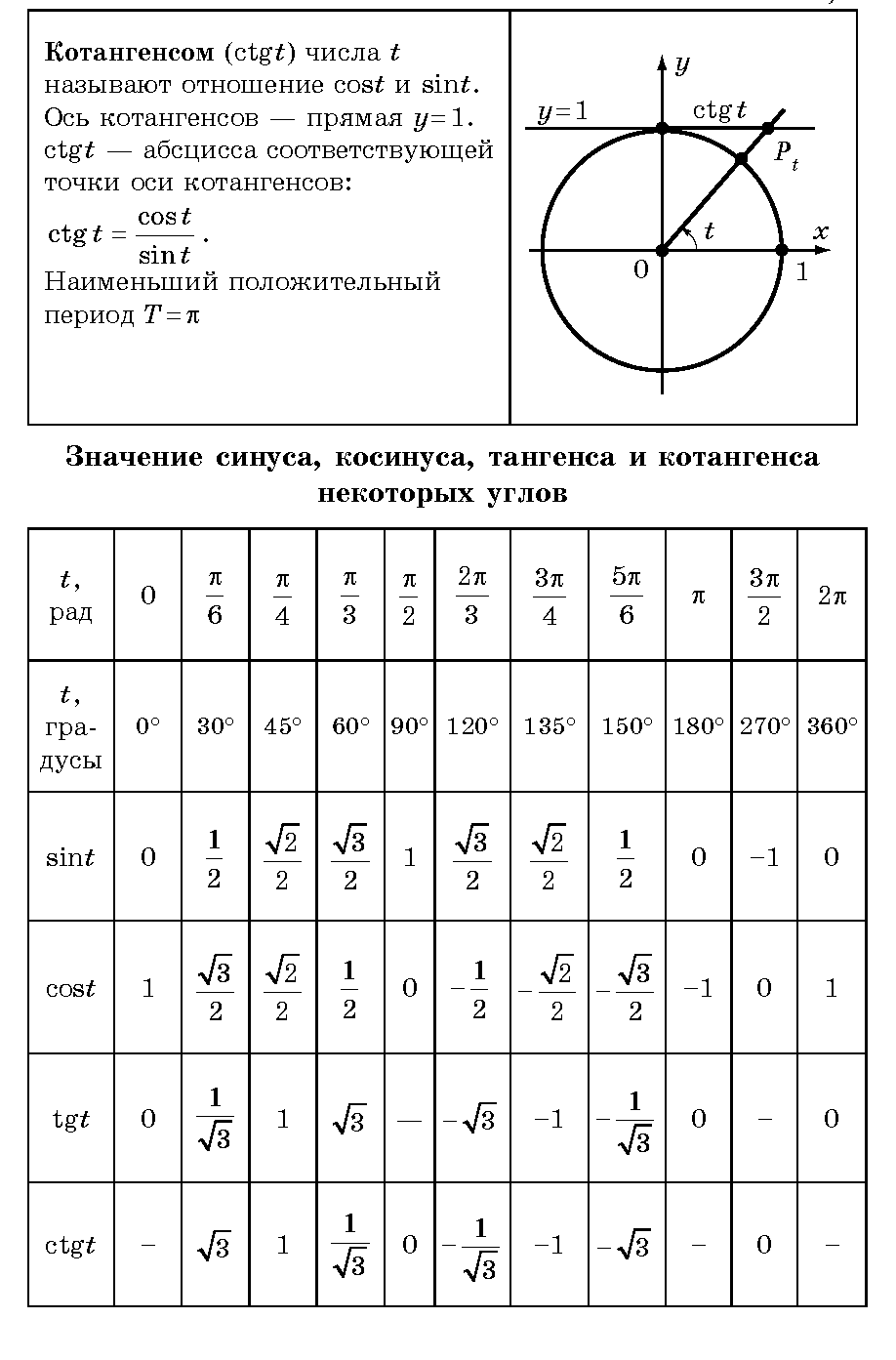
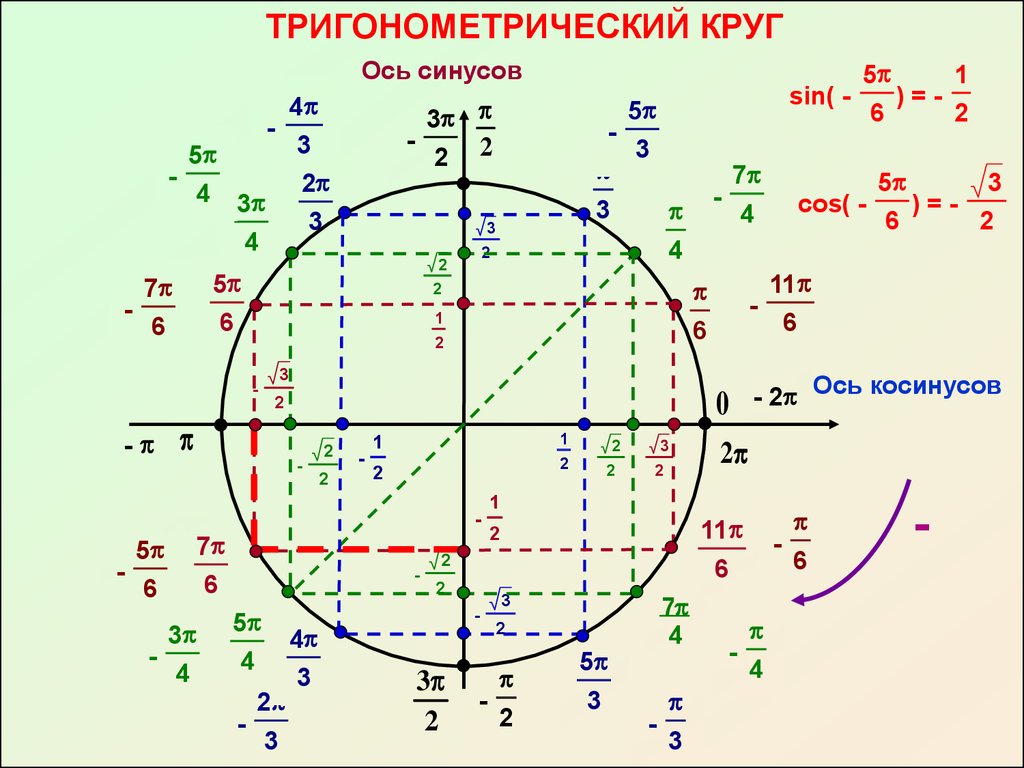 Где же на тригонометрическом круге оси тангенсов и котангенсов? Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через …
Где же на тригонометрическом круге оси тангенсов и котангенсов? Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через …
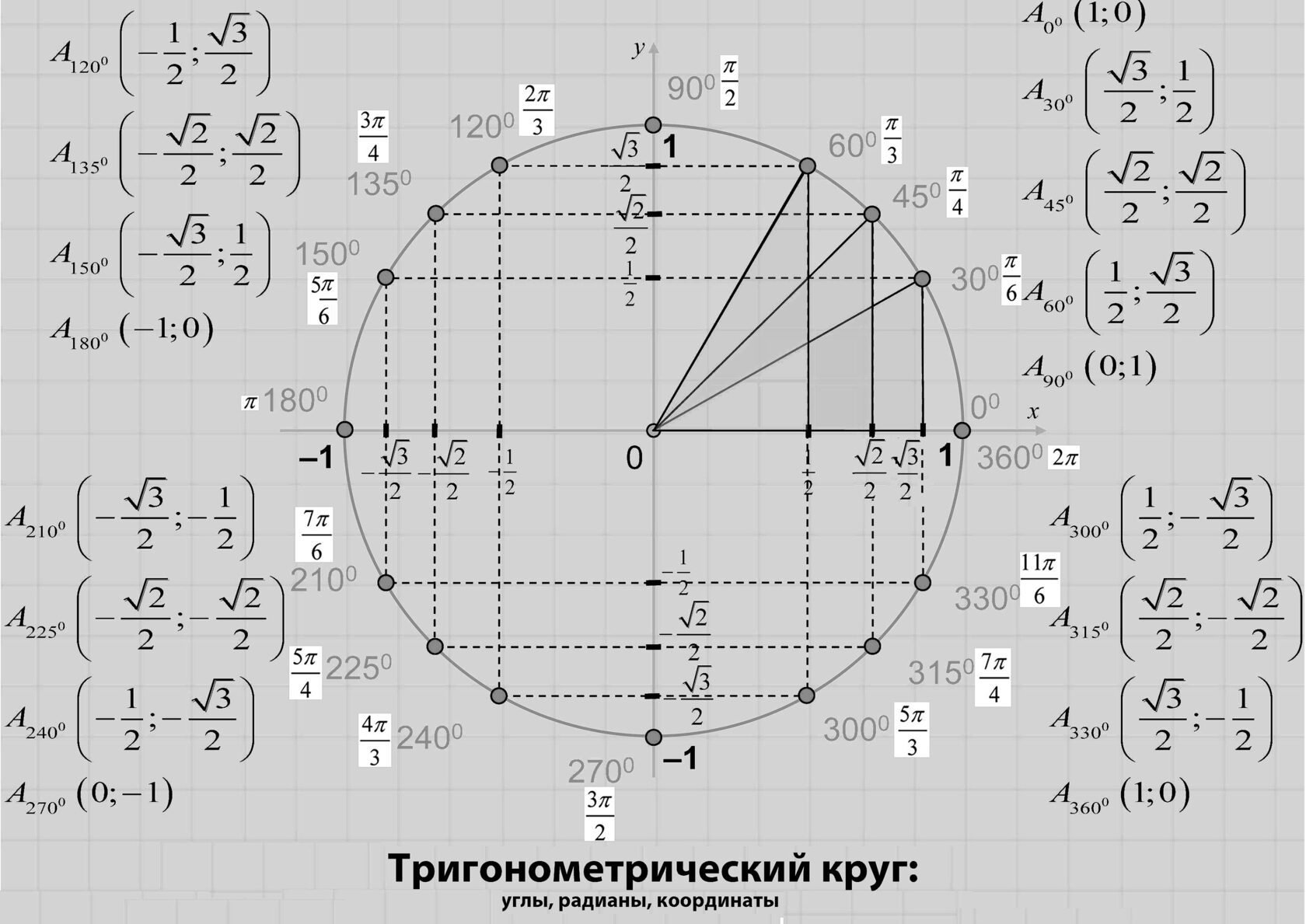
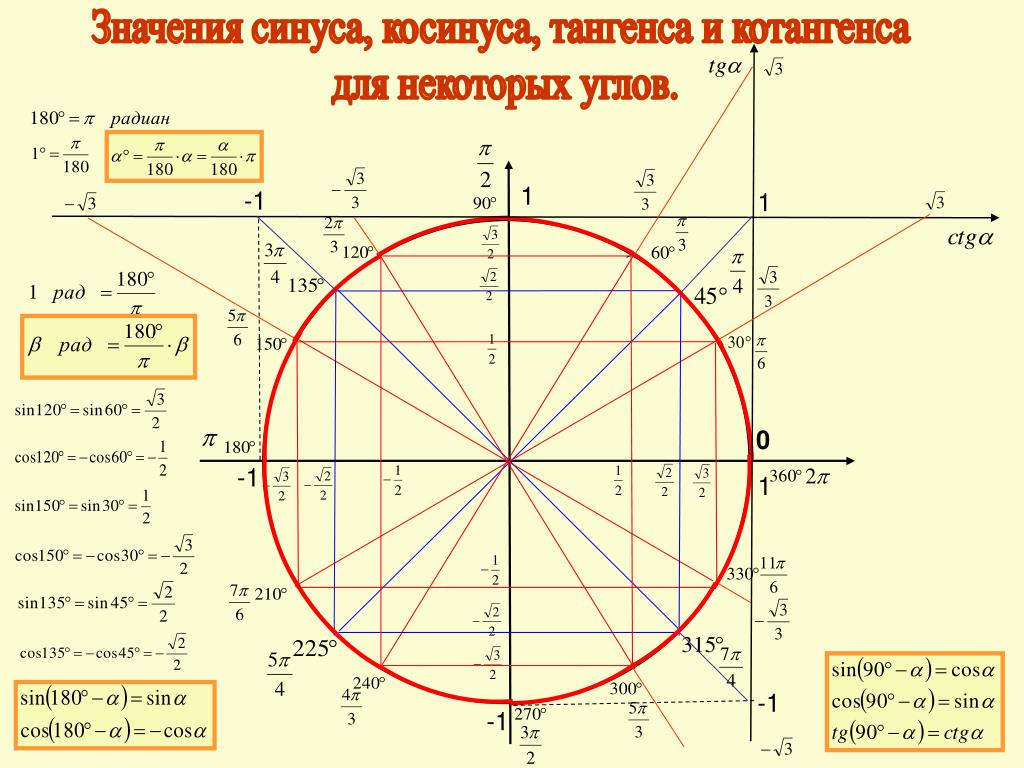 Построение тригонометрического круга. Шаг 1. Проставить основные углы или в градусах (0, 90, 180, 270) или в радианах (0, π/2, π, 3π/2). Точка с координатами (1;0) будет …
Построение тригонометрического круга. Шаг 1. Проставить основные углы или в градусах (0, 90, 180, 270) или в радианах (0, π/2, π, 3π/2). Точка с координатами (1;0) будет …
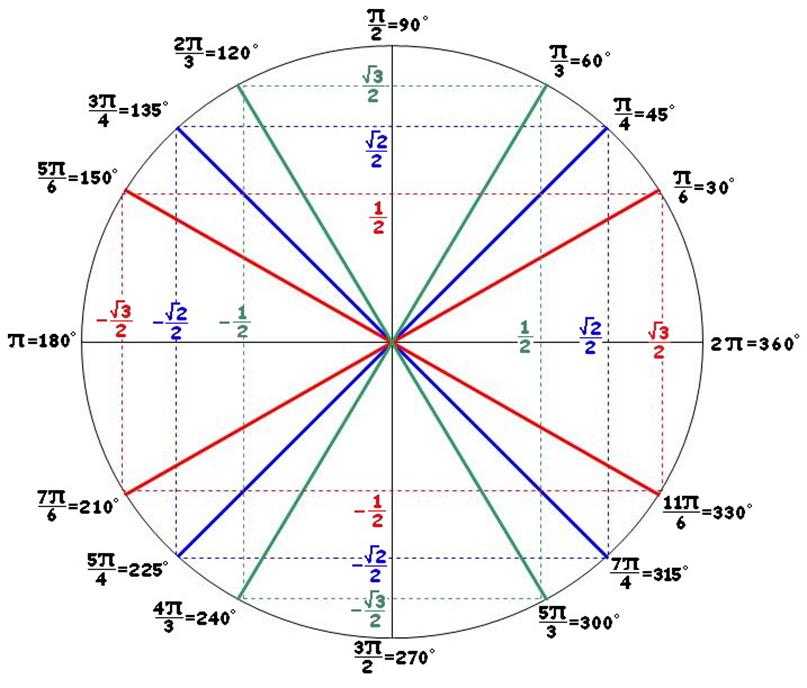
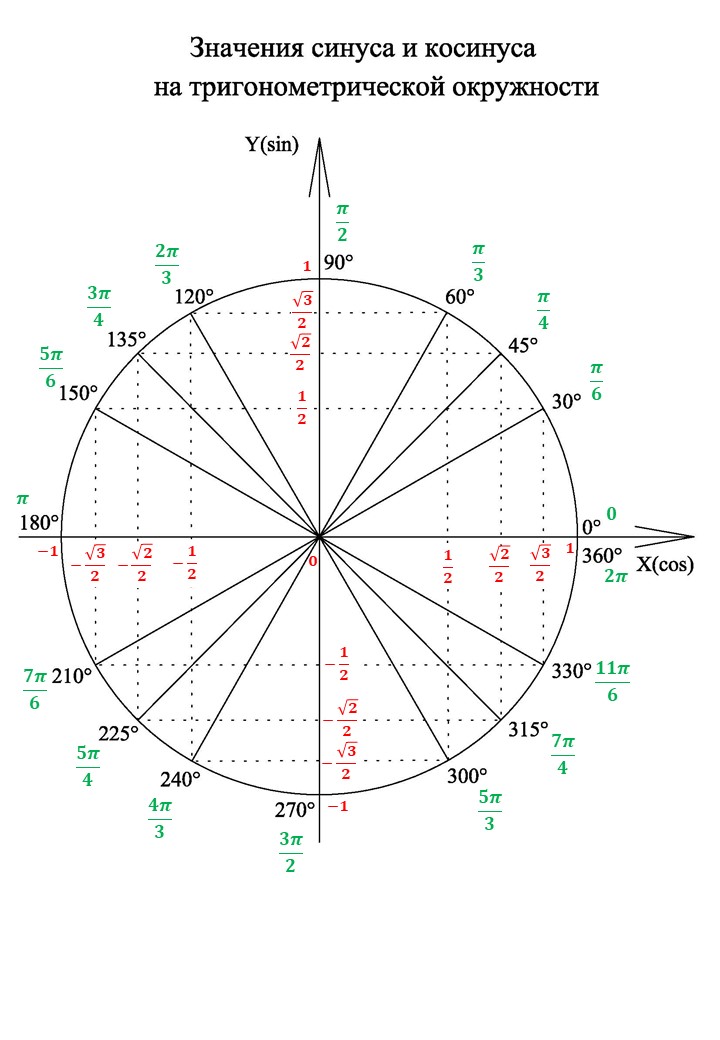
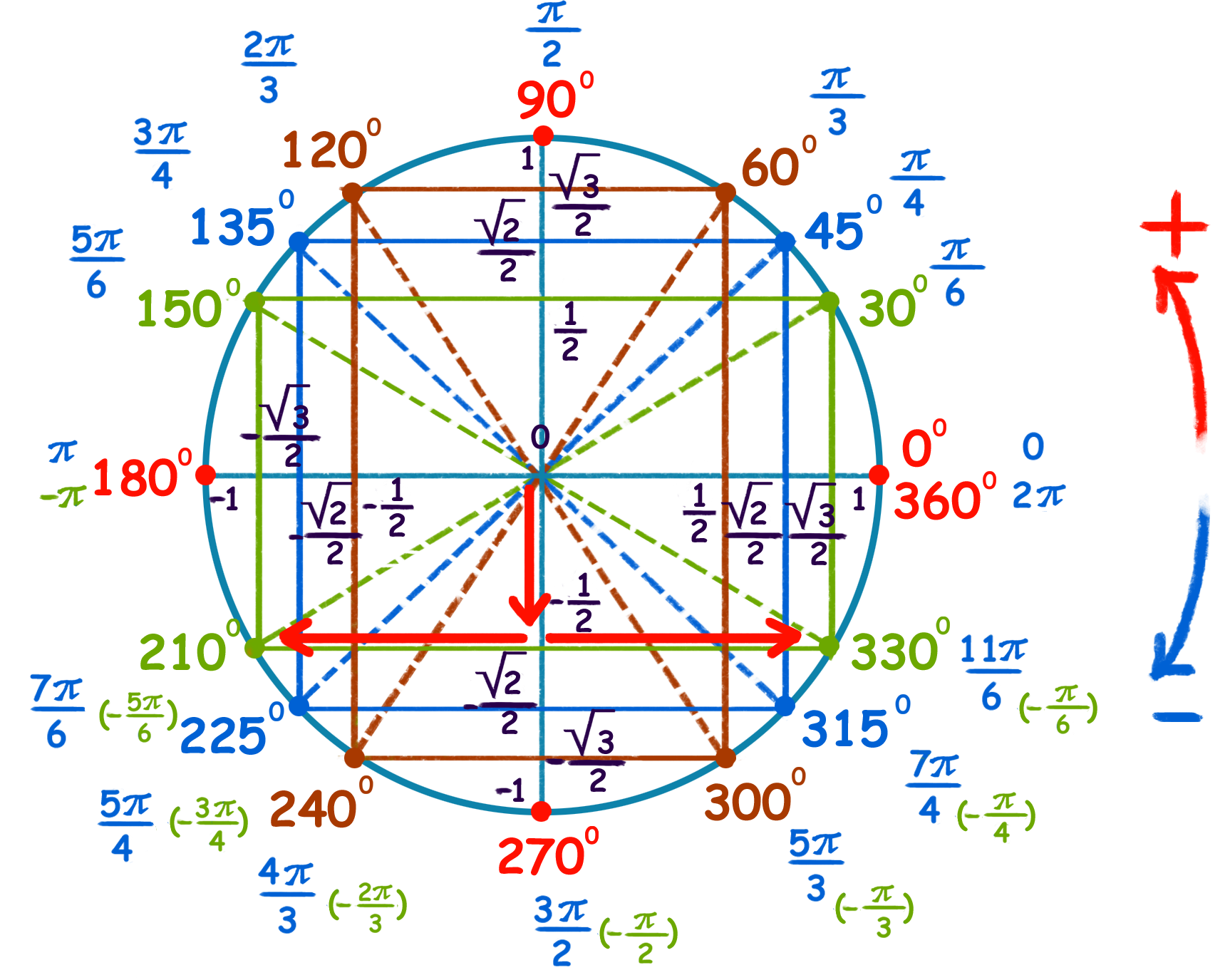
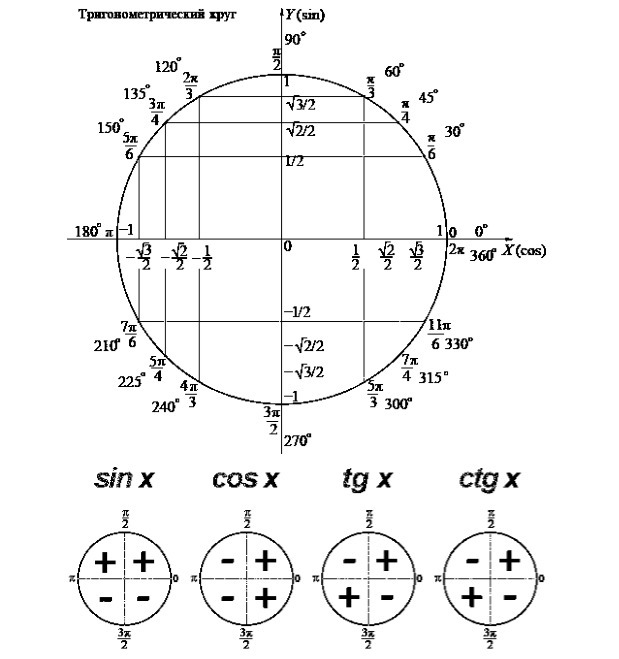
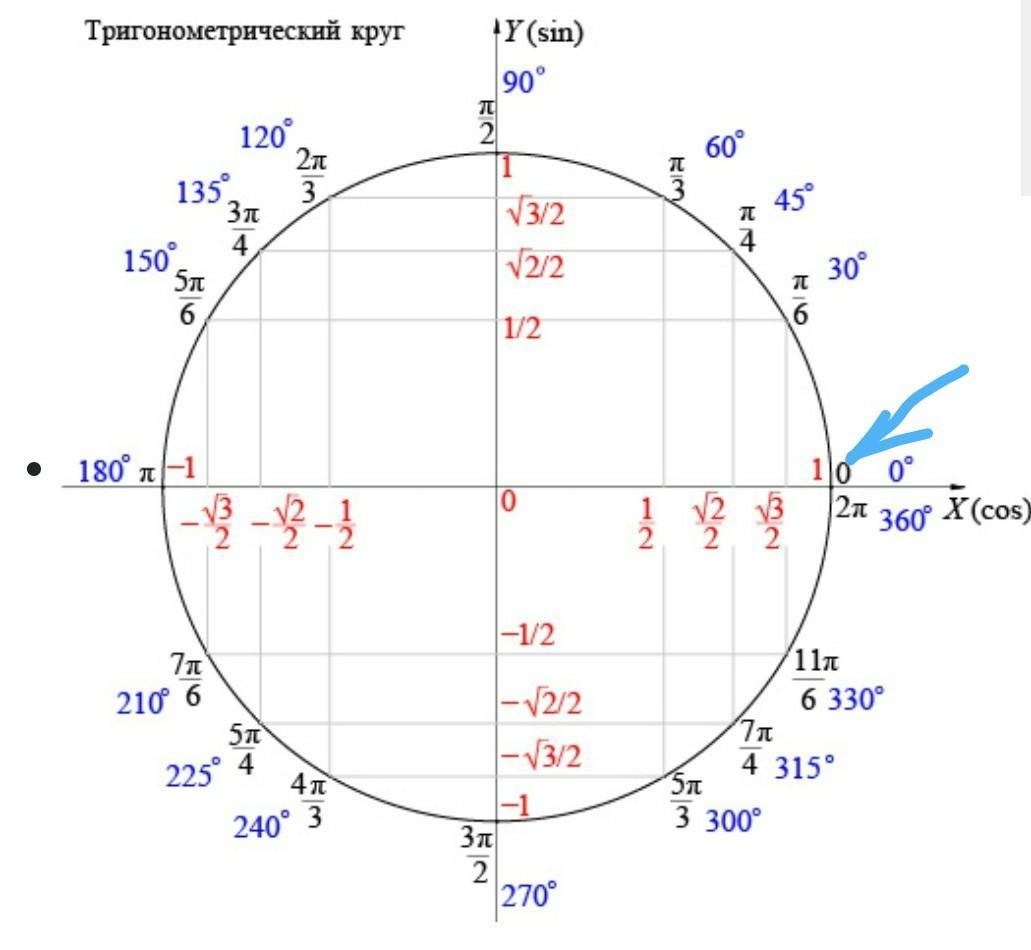 Тригонометрический круг - показано на изображении градусы и значения радиан
Тригонометрический круг - показано на изображении градусы и значения радиан
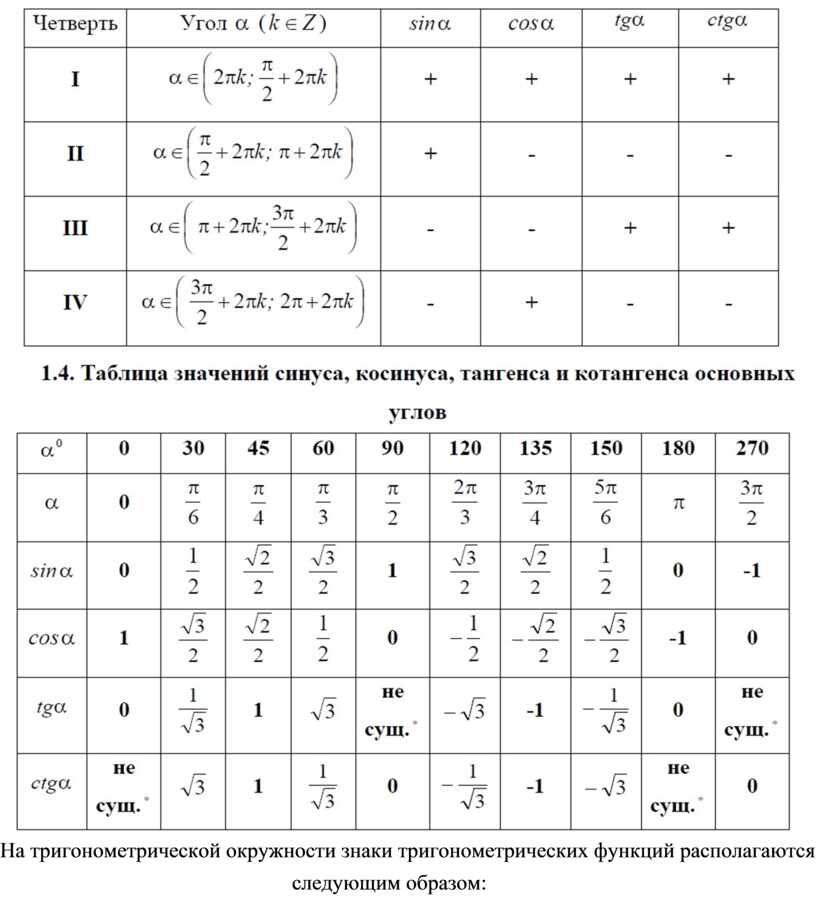 Тригонометрический круг позволяет заменять таблицы значений тригонометрических функций. Также ценностью тригонометрического круга является то, что его всегда …
Тригонометрический круг позволяет заменять таблицы значений тригонометрических функций. Также ценностью тригонометрического круга является то, что его всегда …
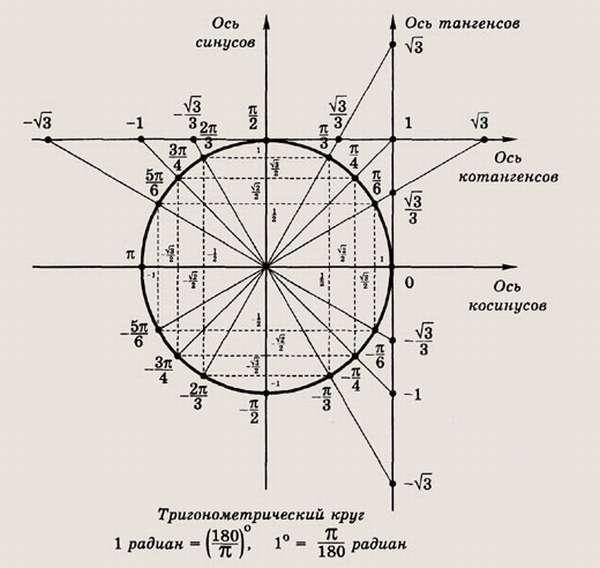 Что такое тригонометрический круг? Он поможет нам вычислять значения тригонометрических функций, не обращаясь к таблице тригонометрических значений.
Что такое тригонометрический круг? Он поможет нам вычислять значения тригонометрических функций, не обращаясь к таблице тригонометрических значений.
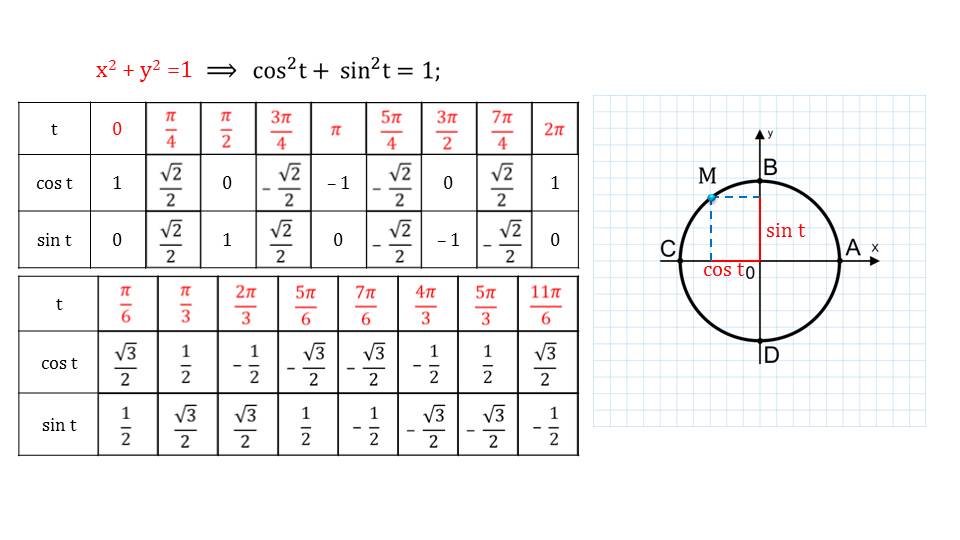
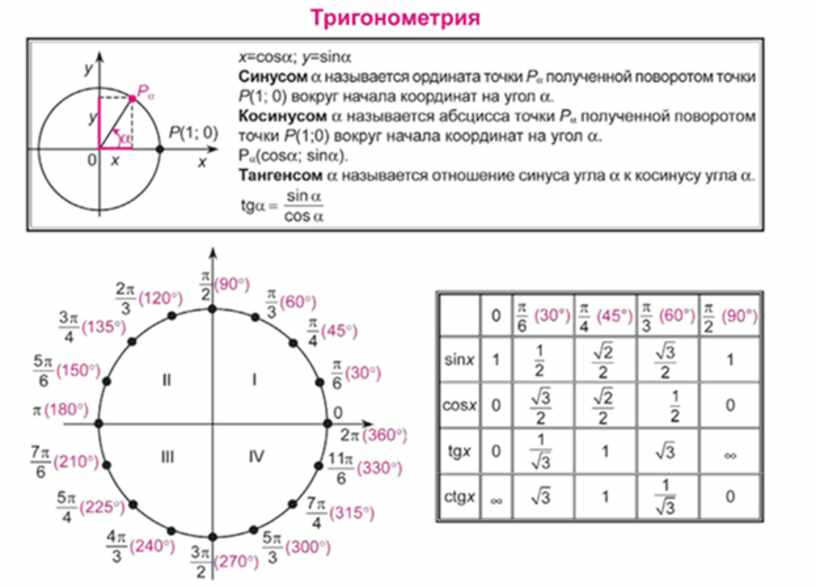
 Тригонометрический круг. Нарисована единичная окружность – то есть окружность с радиусом, равным единицу, и с центром в начале системы координат. Мы отсчитываем …
Тригонометрический круг. Нарисована единичная окружность – то есть окружность с радиусом, равным единицу, и с центром в начале системы координат. Мы отсчитываем …
Еще по теме:








Еще по теме: