i. На каком рисунке изображено множество решений неравенства. В ответе укажите номер правильного варианта. 1) 2) 3) 4) Решение. Решим неравенство:   Корнями урав.
Решение неравенства ax2 + bx + c > 0 или ax2 + bx + c < 0 можно рассматривать как нахождение. решение которого изображено на рисунке. 1) \( x^2-8x0 \) 2) \( x^2-640 \) 3) …
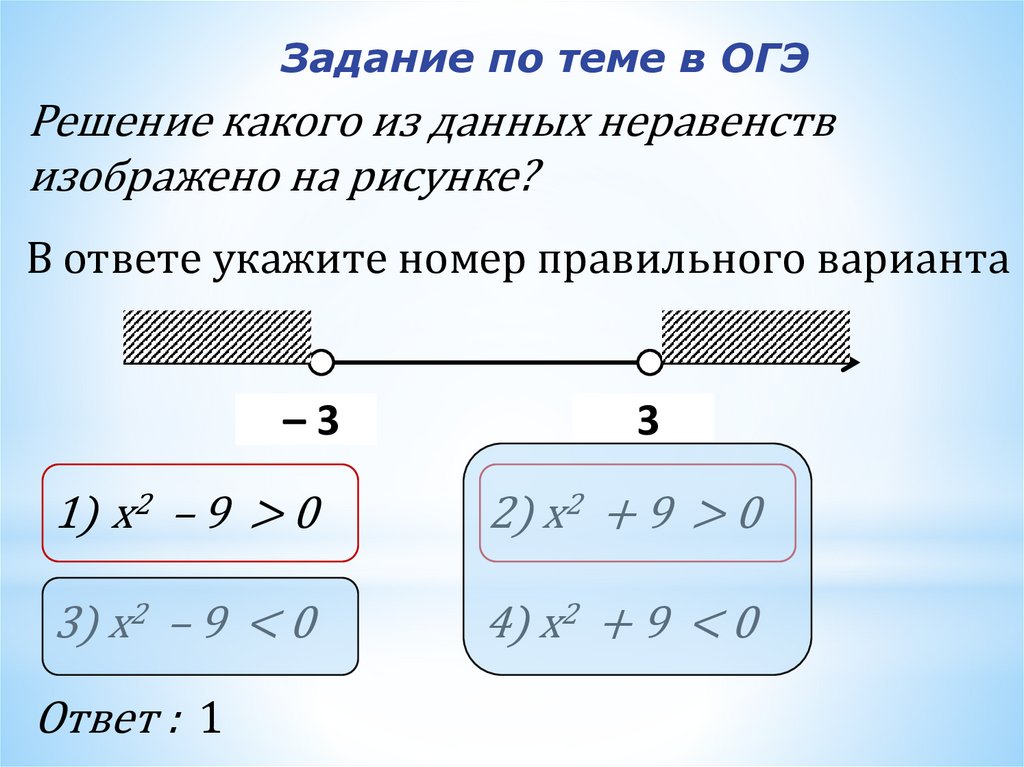
Решение какого из данных неравенств изображено на рисунке? Описание видеоурока: Решение варианта ГИА (ОГЭ) по математике.
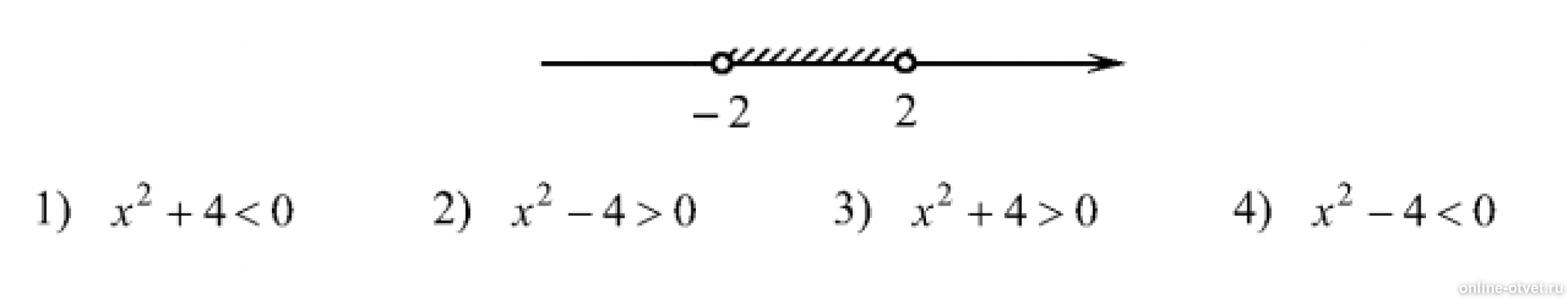Решите систему неравенств На каком рисунке изображено множество её решений? В ответе укажите номер правильного варианта.
Укажите неравенство, решением которого является любое число. В ответе укажите номер правильного варианта. 1) x 2 − 15 0. 2) x 2 + 15 > 0. 3) x 2 + 15 0. 4)
Решите неравенство и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.
На каком рисунке изображено множество решений неравенства ? В ответе укажите номер правильного варианта. 1)
Решение неравенств и систем неравенств с одной переменной. Цели:Совершенствовать умения решать неравенства и системы неравенств, …
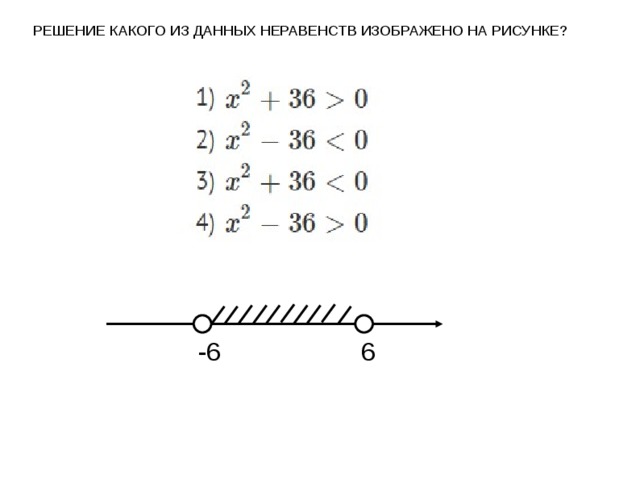Вариант № 320700 1 / 1 РЕШУ ОГЭ — математика Решение какого из данных неравенств изображено на рисунке?
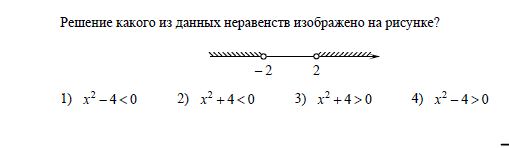Решение какого из данных неравенств изображено на рисунке? Варианты ответа:
Пояснение к заданию №5377. Неравенства вида ax2 + bx + c > 0 и ax2 + bx + c < 0, где x — переменная, a, b и c — некоторые числа и \( a \ne 0, \) называют неравенствами второй …
Поскольку рисунка нет, то мы найдем решение неравенства: 1) x^2 + 13x + 22 ≥ 0. x^2 + 13x + 22 = 0; D = 169 - 88 = 81; x1 = (-13 + 9)/2 = -2; x2 = (-13 - 9)/2 = -11. x принадлежит …
Решение какого из данных неравенств изображено на рисунке? В ответе укажите номер правильного варианта. 1)
Решение какого из данных неравенств изображено на рисунке1)x^2-5x0 ⇔ x(x-5)0 2)x^2-25>0 ⇔(x-5)(x+5)>0
На каком из рисунков изображено множество решений неравенства $8x-5⩾17x+13$?
Решение какого из данных неравенств изображено на рисунке? В ответе укажите номер правильного варианта. 1) 2) 3) 4) Решение. Решим каждое из неравенств: 1) 2) — верно …
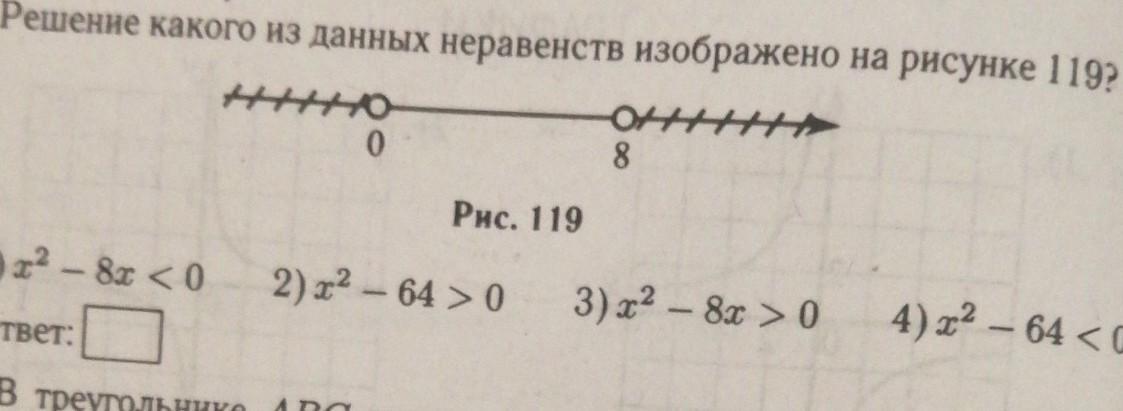
Еще по теме:
