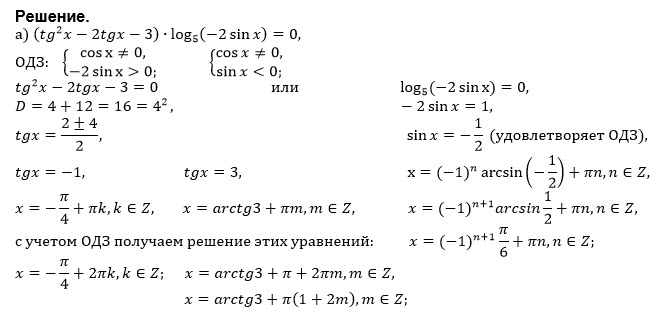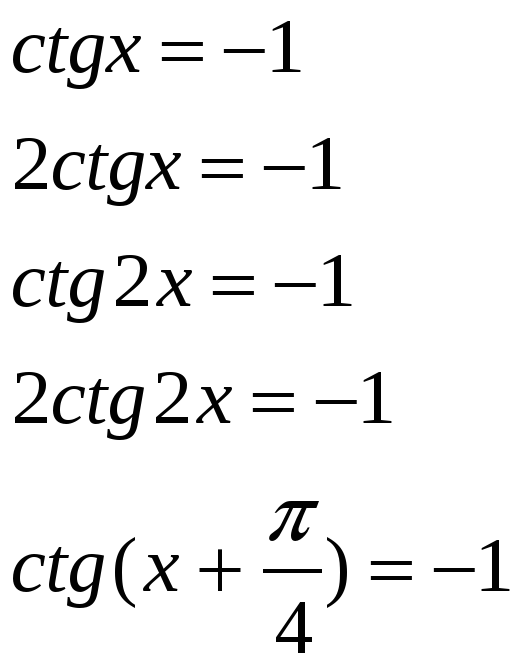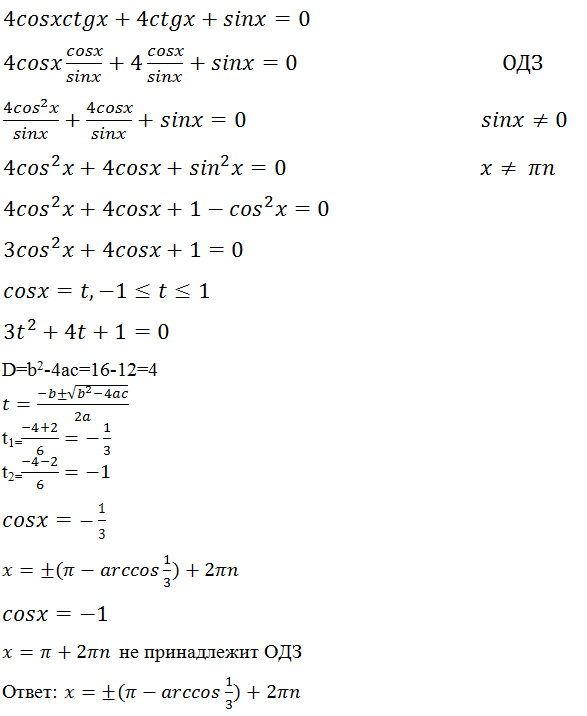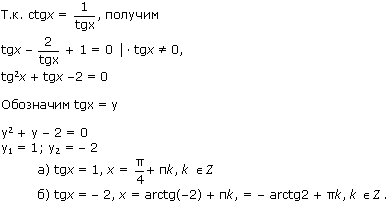\cos (x)-\sin (x)=0 \sin (4\theta)-\frac{\sqrt{3}}{2}=0,\:\forall 0\le\theta<2\pi 2\sin ^2(x)+3=7\sin (x),\:x\in[0,\:2\pi ]
tgx - 2ctgx + 1 = 0; Заменяем ctgx = 1 / tgx; tgx - 2 / tgx + 1 = 0; Умножаем на tgx: tg²x + tgx - 2 = 0; Принимаем tgx = t, получаем: t² + t - 2 = 0; t₁ = - 2; t₂ = 1; 1). tgx = - 2; x₁ = arctg(- 2) + πk, …
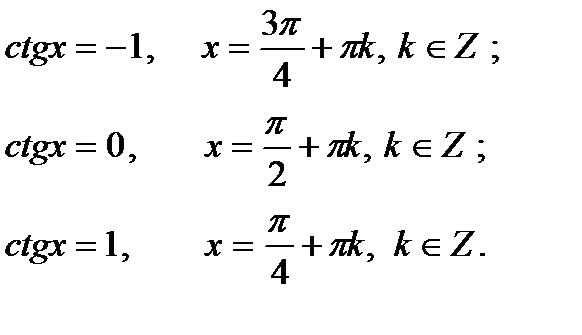Здесь можно решить методом замены переменной. Стоит помнить, что по определению тангенс и котангенс являются обратными функциями, следовательно ctgx=1/tgx. Пусть …
1. Обозначим: tgx = t. Тогда: ctgx = 1/tgx = 1/t. 2. Подставим значения функций в исходное уравнение: tgx - ctgx - 1 = 0; t - 1/t - 1 = 0. 3. Умножим обе части на t: t^2 - 1 - t = 0; t^2 - t - 1 …
Ctg x = 1/tg x. Заменим Ctg x, получим: tg x — 2·1/tg x + 1 = 0 | ·tg x ≠ 0. tg^2 x — 2 + tg x=0. Решаем, как квадратное. tg x = — 2, tg x = 1. x=arc tg (-2) + πk, где k∈Z x = arc tg1 + πk, …
When a product of two or more terms equals zero, then at least one of the terms must be zero. Any solution of term = 0 solves product = 0 as well.
![Tgx-2ctgx=-1 , [0;n/2] - ответ на Uchi.ru - Учи.ру](https://otvet.imgsmail.ru/download/2bd1d2e61caf274be9ce8680dd4163a8_i-532.jpg)
tg^2(x) + tg(x) - 2 = 0. Произведем замену переменных t = tg(x): t^2 + t - 2 = 0. Корни квадратного уравнения вида ax^2 + bx + c = 0 определяются по формуле: x12 = (-b +- …
Можно решить методом замены переменной (по определению тангенс и котангенс являются обратными функциями, отсюда следует, что: ctgx=1/tgx. Пусть tgx=1, а ctgx=1/t. …
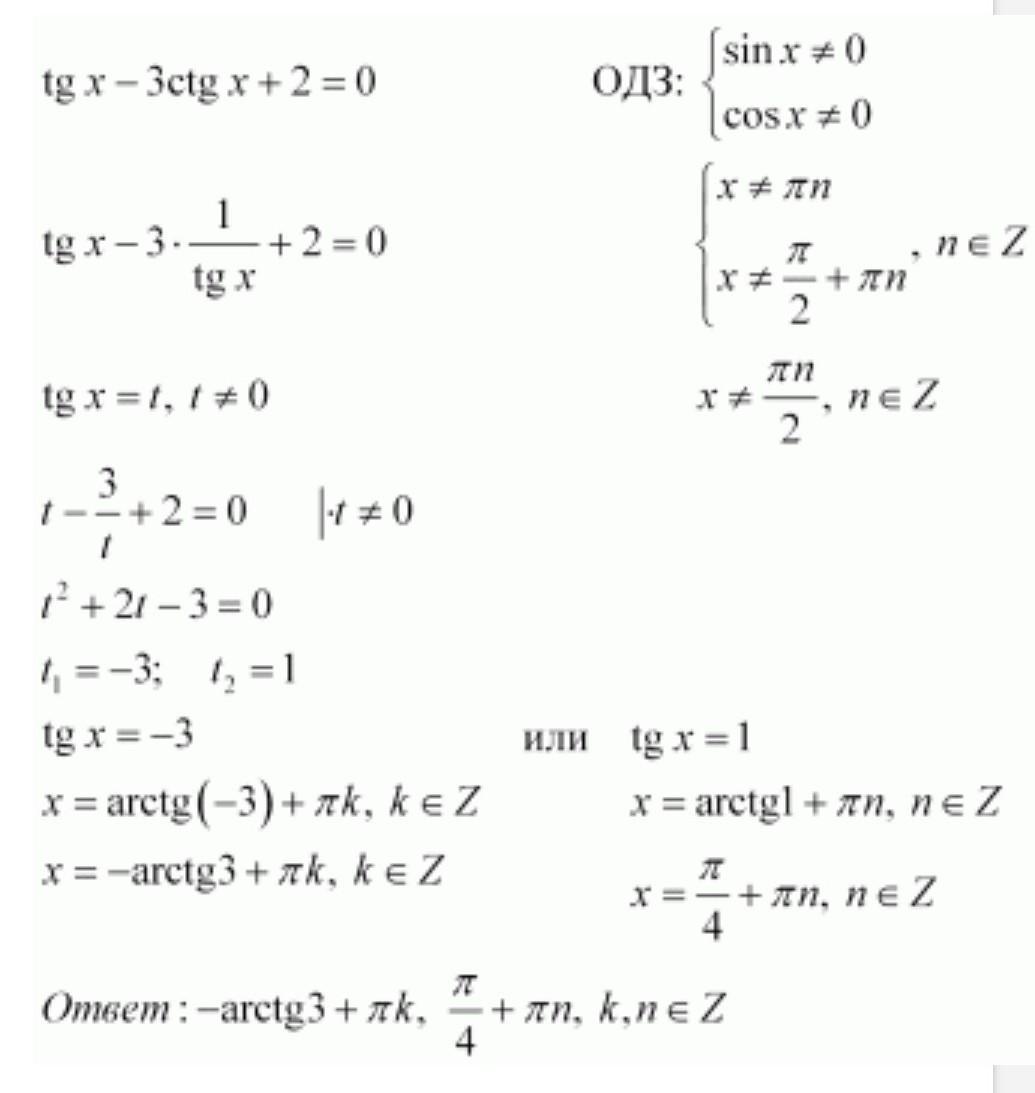x^{2}-x-6=0 -x+3\gt 2x+1 ; line\:(1,\:2),\:(3,\:1) f(x)=x^3 ; prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x) \frac{d}{dx}(\frac{3x+9}{2-x}) (\sin^2(\theta))' \sin(120)
Уравнению (1) соответствуют точки пересечения зеленой пунктирной прямой и единичной окружности. Условие (2) убирает из решения точки, отмеченные красными крестами. …
tg 2 x + tg x -2 = 0; Решаем квадратное уравнение, как от переменной tg x: tg x = (- 1 ± √ (1 +8)) / 2 = (- 1 ± 3) / 2;
получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). Решение не …
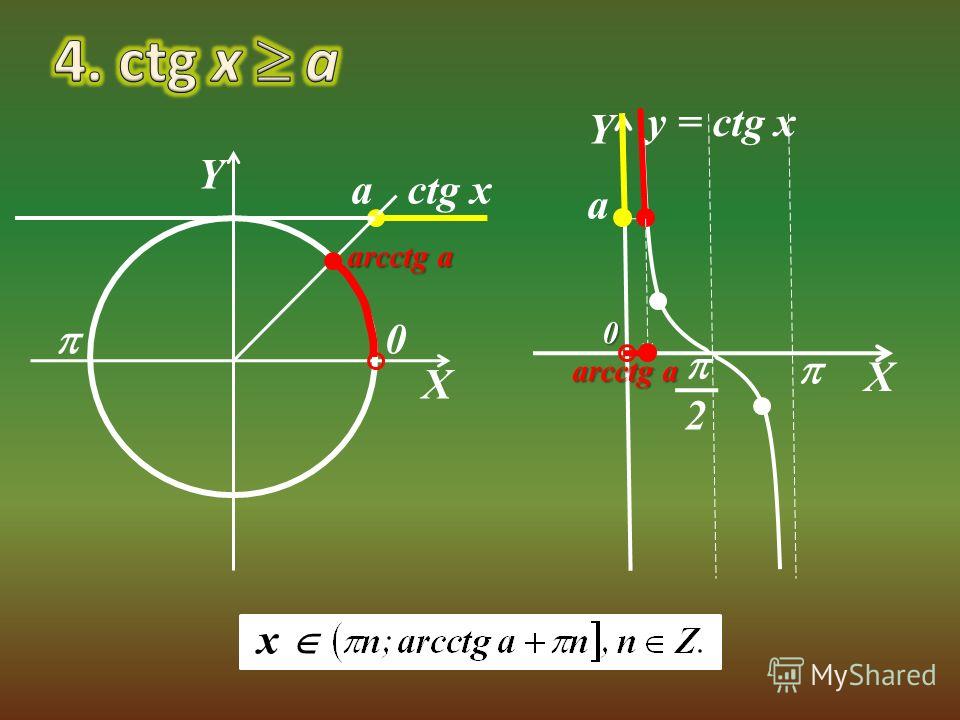
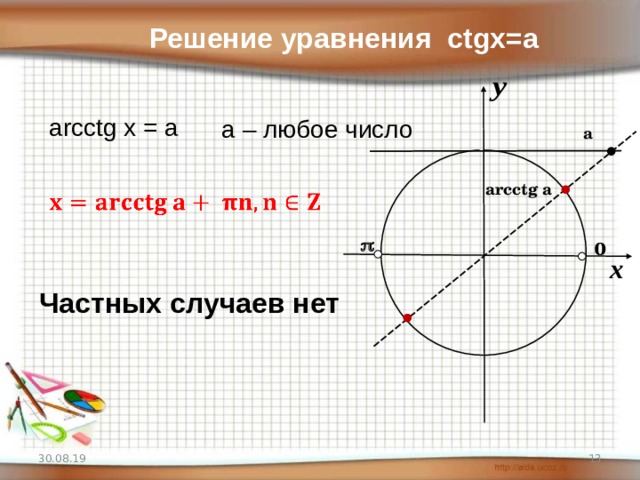
Арктангенс и решение уравнения tgx = a, арккотангенс и решение уравнения ctgx = a. Тригонометрические уравнения (два основных метода решения …
Приведем уравнение к стандартному виду квадратного уравнения, применив основное тождество ctgx * tgx = 1: 2сtgx + 3tgx + 5 = 0;
6) ctgx=-1 x=(П-П/4)+Пn Приведем выражение в скобках к общему знаменателю: П-П/4= 4П-П/4 (дробная черта общая для всех чисел) = 3П/4. х=3П/4+Пn, n э Z.
Еще по теме:
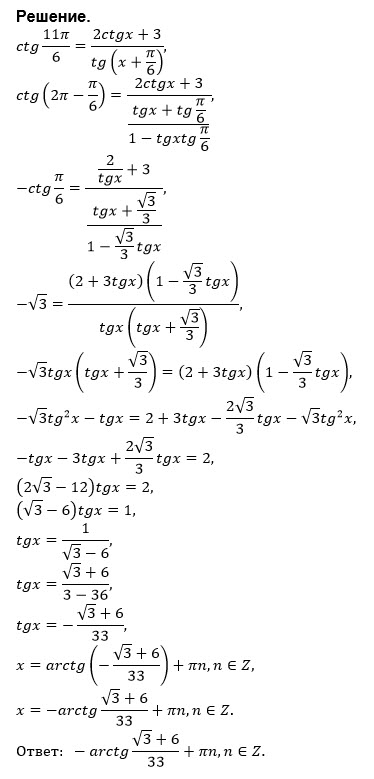
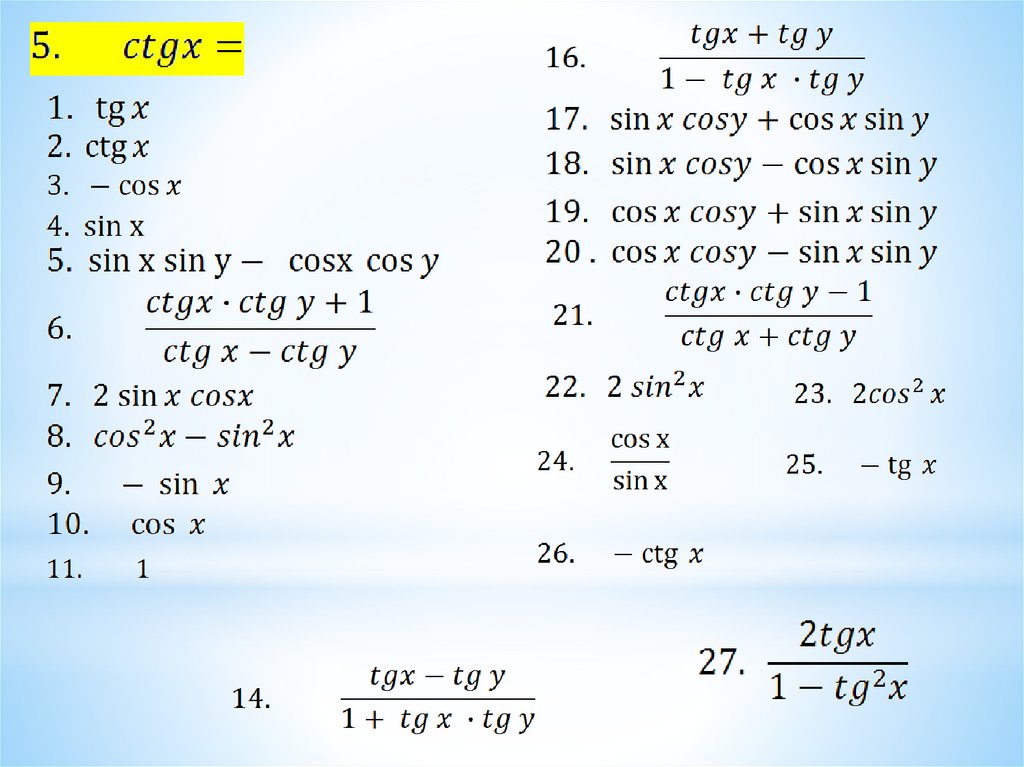
Еще по теме:
