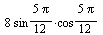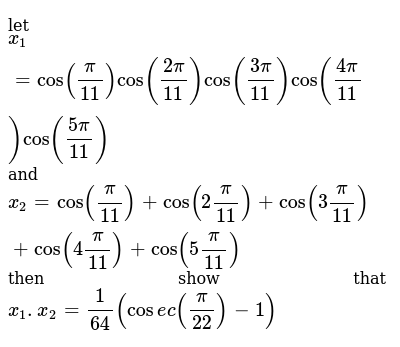5sin(11pi/12)*cos(11pi/12) = 5 sin(2*11pi/12)/2 = 5/2*sin(11pi/6) = = 5/2*sin(2pi - pi/6)= -5/2*sin(pi/6) =-5/2*1/2 = -1,25
5sin(11pi/12)*cos(11pi/12) = 5 sin(2*11pi/12)/2 = 5/2*sin(11pi/6) = = 5/2*sin(2pi - pi/6)= -5/2*sin(pi/6) =-5/2*1/2 = -1,25
 Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Make the expression negative because cosine is negative in the second quadrant. −cos(π 12) …
Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Make the expression negative because cosine is negative in the second quadrant. −cos(π 12) …
 First, split the angle into two angles where the values of the six trigonometric functions are known. In this case, 11π 12 11 π 12 can be split into 2π 3 + π 4 2 π 3 + π 4. cos(2π 3 + π 4) cos (2 π …
First, split the angle into two angles where the values of the six trigonometric functions are known. In this case, 11π 12 11 π 12 can be split into 2π 3 + π 4 2 π 3 + π 4. cos(2π 3 + π 4) cos (2 π …
 Sin 11pi/12 degrees is the value of sine trigonometric function for an angle equal to 11pi/12. Understand methods to find the value of sin 11pi/12 with examples and FAQs.
Sin 11pi/12 degrees is the value of sine trigonometric function for an angle equal to 11pi/12. Understand methods to find the value of sin 11pi/12 with examples and FAQs.
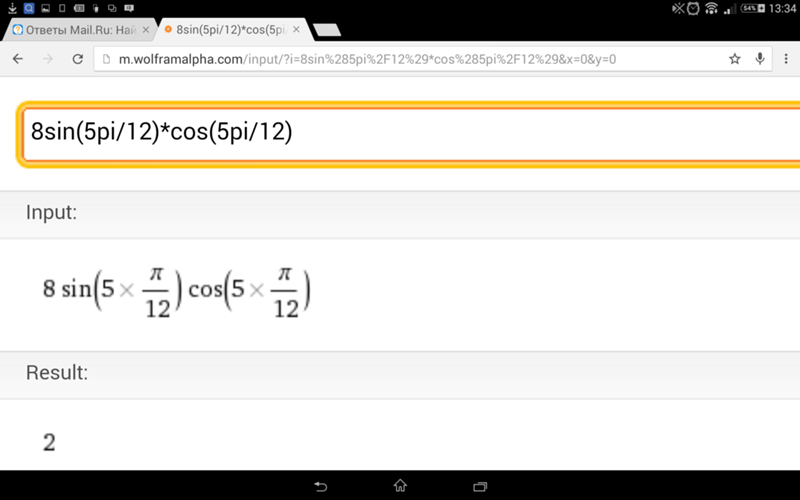 The key here is to break up 11pi/12 into a sum or difference of fractions. Knowing this is our intermediate goal we want to find common frations of pi (e.g. pi/2, pi/3, pi/4 and …
The key here is to break up 11pi/12 into a sum or difference of fractions. Knowing this is our intermediate goal we want to find common frations of pi (e.g. pi/2, pi/3, pi/4 and …
 Use a half-angle formula to find sin (11π/12). sin (11π/12) = sin (π/12) = √ (1 - cos (π/6))/2 = √ (2 - √3)/2. half angle formula for sines is. sin (x/2) = + or - sqr ( (1-cosx)/2) sin …
Use a half-angle formula to find sin (11π/12). sin (11π/12) = sin (π/12) = √ (1 - cos (π/6))/2 = √ (2 - √3)/2. half angle formula for sines is. sin (x/2) = + or - sqr ( (1-cosx)/2) sin …
 Trigonometry is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle …
Trigonometry is a branch of mathematics concerned with relationships between angles and side lengths of triangles. In particular, the trigonometric functions relate the angles of a right triangle …
 To solve a trigonometric simplify the equation using trigonometric identities. Then, write the equation in a standard form, and isolate the variable using algebraic manipulation to solve for …
To solve a trigonometric simplify the equation using trigonometric identities. Then, write the equation in a standard form, and isolate the variable using algebraic manipulation to solve for …
Еще по теме:

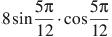




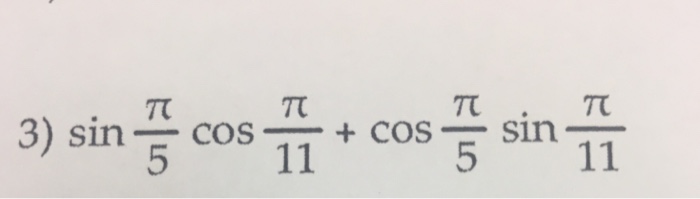

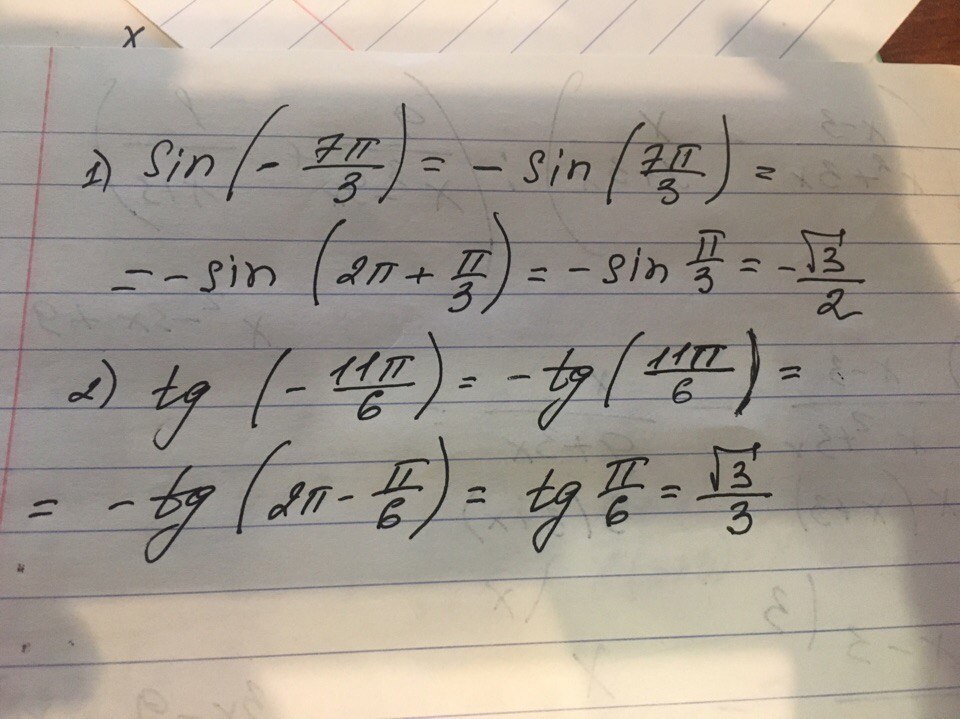



Еще по теме: